寫在前面 整個項目都托管在了 Github 上: 查找更為方便的版本見: 這一節內容可能會用到的庫文件有 PriorityQueue,同樣在 Github 上可以找到。 善用 Ctrl + F 查找題目。 習題&題解 2.4.1 題目 用序列 P R I O R I T Y Q U E U E (字 ...
寫在前面
整個項目都托管在了 Github 上:https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp
查找更為方便的版本見:https://alg4.ikesnowy.com/
這一節內容可能會用到的庫文件有 PriorityQueue,同樣在 Github 上可以找到。
善用 Ctrl + F 查找題目。
習題&題解
2.4.1
題目
用序列 P R I O * R * * I * T * Y * * * Q U E * * * U * E
(字母表示插入元素,星號表示刪除最大元素)
操作一個初始為空的優先隊列。
給出每次刪除最大元素返回的字元。
解答
R R P O T Y I I U Q E U優先隊列的變化如下:
| 輸入命令 | 優先隊列 | 輸出 |
|---|---|---|
| P | P | |
| R | P R | |
| I | P R I | |
| O | P R I O | |
| * | P I O | R |
| R | P I O R | |
| * | P I O | R |
| * | I O | P |
| I | I O I | |
| * | I I | O |
| T | I I T | |
| * | I I | T |
| Y | I I Y | |
| * | I I | Y |
| * | I | I |
| * | I | |
| Q | Q | |
| U | Q U | |
| E | Q U E | |
| * | Q E | U |
| * | E | Q |
| * | E | |
| U | U | |
| * | U | |
| E | E |
2.4.2
題目
分析以下說法:
要實現在常數時間找到最大元素,
為何不用一個棧或者隊列,
然後記錄已插入的最大元素併在找出最大元素時返回它的值。
解答
這種方式只能取出一次最大值,這個最大值就是輸入序列裡面的最大值。
當需要繼續取出最大值時(即繼續取第二大、第三大、第 i 大的元素),
這個方法就不再適用了(或者說不能在常數時間內完成)。
2.4.3
題目
用以下數據結構實現優先隊列,支持插入元素和刪除最大元素操作:
無序數組、有序數組、無序鏈表和鏈表。
將你的 4 種實現中每種操作在最壞情況下的運行時間上下限製成一張表格。
解答
有序數組的官方版本:https://algs4.cs.princeton.edu/24pq/OrderedArrayMaxPQ.java.html
無序數組的官方版本:https://algs4.cs.princeton.edu/24pq/UnorderedArrayMaxPQ.java.html
| 實現 | insert() | delMax() |
|---|---|---|
| 有序數組 | N | 1 |
| 有序鏈表 | N | 1 |
| 無序數組 | 1 | N |
| 無序鏈表 | 1 | N |
在庫文件中定義瞭如下介面,所有的(最大)優先隊列都會實現它。
using System;
namespace PriorityQueue
{
/// <summary>
/// 實現優先隊列 API 的介面。
/// </summary>
/// <typeparam name="Key">優先隊列容納的元素。</typeparam>
public interface IMaxPQ<Key> where Key : IComparable<Key>
{
/// <summary>
/// 向優先隊列中插入一個元素。
/// </summary>
/// <param name="v">插入元素的類型。</param>
void Insert(Key v);
/// <summary>
/// 返回最大元素。
/// </summary>
/// <returns></returns>
Key Max();
/// <summary>
/// 刪除並返回最大元素。
/// </summary>
/// <returns></returns>
Key DelMax();
/// <summary>
/// 返回隊列是否為空。
/// </summary>
/// <returns></returns>
bool IsEmpty();
/// <summary>
/// 返回隊列中的元素個數。
/// </summary>
/// <returns></returns>
int Size();
}
}於是我們就可以使用這樣的方法測試所有類型的優先隊列:
static void test(IMaxPQ<string> pq)
{
Console.WriteLine(pq.ToString());
pq.Insert("this");
pq.Insert("is");
pq.Insert("a");
pq.Insert("test");
while (!pq.IsEmpty())
Console.Write(pq.DelMax() + " ");
Console.WriteLine();
}代碼
給出鏈表的實現,基於數組的實現可以點擊「另請參閱」中的 PriorityQueue 庫查看。
無序鏈表
using System;
namespace PriorityQueue
{
/// <summary>
/// 不保持元素輸入順序的優先隊列。(基於鏈表)
/// </summary>
/// <typeparam name="Key">優先隊列中的元素類型。</typeparam>
public class UnorderedLinkedMaxPQ<Key> : IMaxPQ<Key> where Key : IComparable<Key>
{
/// <summary>
/// 保存元素的鏈表。
/// </summary>
private readonly LinkedList<Key> pq;
/// <summary>
/// 預設構造函數,建立一條優先隊列。
/// </summary>
public UnorderedLinkedMaxPQ()
{
this.pq = new LinkedList<Key>();
}
/// <summary>
/// 獲得(但不刪除)優先隊列中的最大元素。
/// </summary>
/// <returns></returns>
public Key Max()
{
int max = 0;
for (int i = 1; i < this.pq.Size(); i++)
if (Less(this.pq.Find(max), this.pq.Find(i)))
max = i;
return this.pq.Find(max);
}
/// <summary>
/// 返回並刪除優先隊列中的最大值。
/// </summary>
/// <returns></returns>
public Key DelMax()
{
int max = 0;
for (int i = 1; i < this.pq.Size(); i++)
if (Less(this.pq.Find(max), this.pq.Find(i)))
max = i;
return this.pq.Delete(max);
}
/// <summary>
/// 向優先隊列中插入一個元素。
/// </summary>
/// <param name="v">需要插入的元素。</param>
public void Insert(Key v) => this.pq.Insert(v);
/// <summary>
/// 檢查優先隊列是否為空。
/// </summary>
/// <returns></returns>
public bool IsEmpty() => this.pq.IsEmpty();
/// <summary>
/// 檢查優先隊列中含有的元素數量。
/// </summary>
/// <returns></returns>
public int Size() => this.pq.Size();
/// <summary>
/// 比較第一個元素是否小於第二個元素。
/// </summary>
/// <param name="a">第一個元素。</param>
/// <param name="b">第二個元素。</param>
/// <returns></returns>
private bool Less(Key a, Key b) => a.CompareTo(b) < 0;
}
}有序鏈表
using System;
namespace PriorityQueue
{
/// <summary>
/// 元素保持輸入順序的優先隊列。(基於鏈表)
/// </summary>
/// <typeparam name="Key">優先隊列中的元素類型。</typeparam>
public class OrderedLinkedMaxPQ<Key> : IMaxPQ<Key> where Key : IComparable<Key>
{
/// <summary>
/// 用於保存元素的鏈表。
/// </summary>
private readonly LinkedList<Key> pq;
/// <summary>
/// 預設構造函數,建立一條優先隊列。
/// </summary>
public OrderedLinkedMaxPQ()
{
this.pq = new LinkedList<Key>();
}
/// <summary>
/// 向優先隊列中插入一個元素。
/// </summary>
/// <param name="v">需要插入的元素。</param>
public void Insert(Key v)
{
int i = this.pq.Size() - 1;
while (i >= 0 && Less(v, this.pq.Find(i)))
i--;
this.pq.Insert(v, i + 1);
}
/// <summary>
/// 返回並刪除優先隊列中的最大值。
/// </summary>
/// <returns></returns>
public Key DelMax() => this.pq.Delete(this.pq.Size() - 1);
/// <summary>
/// 檢查優先隊列是否為空。
/// </summary>
/// <returns></returns>
public bool IsEmpty() => this.pq.IsEmpty();
/// <summary>
/// 獲得(但不刪除)優先隊列中的最大元素。
/// </summary>
/// <returns></returns>
public Key Max() => this.pq.Find(this.pq.Size() - 1);
/// <summary>
/// 檢查優先隊列中含有的元素數量。
/// </summary>
/// <returns></returns>
public int Size() => this.pq.Size();
/// <summary>
/// 比較第一個元素是否小於第二個元素。
/// </summary>
/// <param name="a">第一個元素。</param>
/// <param name="b">第二個元素。</param>
/// <returns></returns>
private bool Less(Key a, Key b) => a.CompareTo(b) < 0;
}
}另請參閱
2.4.4
題目
一個按降序排列的數組也是一個面向最大元素的堆嗎?
解答
是的。
例如這個數組:9 8 7 6 5,畫成二叉堆如下:
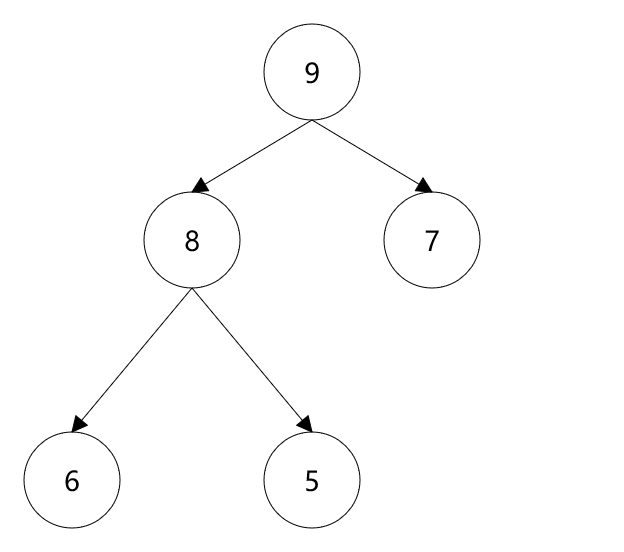
2.4.5
題目
將 E A S Y Q U E S T I O N 順序插入一個面向最大元素的堆中,給出結果。
解答

2.4.6
題目
按照練習 2.4.1 的規則,
用序列 P R I O * R * * I * T * Y * * * Q U E * * * U * E 操作一個初始空間為空的面向最大元素的堆,
給出每次操作後堆的內容。
解答
官方給出的最大堆實現:https://algs4.cs.princeton.edu/24pq/MaxPQ.java.html
運行示意圖:

運行結果:
P
R P
R P I
R P O I
P O I
R P O I
P O I
O I
O I I
I I
T I I
I I
Y I I
I I
I
Q
U Q
U Q E
Q E
E
U
E代碼
最大堆的實現
using System;
using System.Collections;
using System.Collections.Generic;
namespace PriorityQueue
{
/// <summary>
/// 最大堆。(數組實現)
/// </summary>
/// <typeparam name="Key">最大堆中保存的元素。</typeparam>
public class MaxPQ<Key> : IMaxPQ<Key>, IEnumerable<Key> where Key : IComparable<Key>
{
private Key[] pq; // 保存元素的數組。
private int n; // 堆中的元素數量。
/// <summary>
/// 預設構造函數。
/// </summary>
public MaxPQ() : this(1) { }
/// <summary>
/// 建立指定容量的最大堆。
/// </summary>
/// <param name="capacity">最大堆的容量。</param>
public MaxPQ(int capacity)
{
this.pq = new Key[capacity];
this.n = 0;
}
/// <summary>
/// 刪除並返回最大元素。
/// </summary>
/// <returns></returns>
public Key DelMax()
{
if (IsEmpty())
throw new ArgumentOutOfRangeException("Priority Queue Underflow");
Key max = this.pq[1];
Exch(1, this.n--);
Sink(1);
this.pq[this.n + 1] = default(Key);
if ((this.n > 0) && (this.n == this.pq.Length / 4))
Resize(this.pq.Length / 2);
return max;
}
/// <summary>
/// 向堆中插入一個元素。
/// </summary>
/// <param name="v">需要插入的元素。</param>
public void Insert(Key v)
{
if (this.n == this.pq.Length - 1)
Resize(2 * this.pq.Length);
this.pq[++this.n] = v;
Swim(this.n);
}
/// <summary>
/// 檢查堆是否為空。
/// </summary>
/// <returns></returns>
public bool IsEmpty() => this.n == 0;
/// <summary>
/// 獲得堆中最大元素。
/// </summary>
/// <returns></returns>
public Key Max() => this.pq[1];
/// <summary>
/// 獲得堆中元素的數量。
/// </summary>
/// <returns></returns>
public int Size() => this.n;
/// <summary>
/// 獲取堆的迭代器,元素以降序排列。
/// </summary>
/// <returns></returns>
public IEnumerator<Key> GetEnumerator()
{
MaxPQ<Key> copy = new MaxPQ<Key>(this.n);
for (int i = 1; i <= this.n; i++)
copy.Insert(this.pq[i]);
while (!copy.IsEmpty())
yield return copy.DelMax(); // 下次迭代的時候從這裡繼續執行。
}
/// <summary>
/// 獲取堆的迭代器,元素以降序排列。
/// </summary>
/// <returns></returns>
IEnumerator IEnumerable.GetEnumerator()
{
return GetEnumerator();
}
/// <summary>
/// 使元素上浮。
/// </summary>
/// <param name="k">需要上浮的元素。</param>
private void Swim(int k)
{
while (k > 1 && Less(k / 2, k))
{
Exch(k, k / 2);
k /= 2;
}
}
/// <summary>
/// 使元素下沉。
/// </summary>
/// <param name="k">需要下沉的元素。</param>
private void Sink(int k)
{
while (k * 2 <= this.n)
{
int j = 2 * k;
if (j < this.n && Less(j, j + 1))
j++;
if (!Less(k, j))
break;
Exch(k, j);
k = j;
}
}
/// <summary>
/// 重新調整堆的大小。
/// </summary>
/// <param name="capacity">調整後的堆大小。</param>
private void Resize(int capacity)
{
Key[] temp = new Key[capacity];
for (int i = 1; i <= this.n; i++)
{
temp[i] = this.pq[i];
}
this.pq = temp;
}
/// <summary>
/// 判斷堆中某個元素是否小於另一元素。
/// </summary>
/// <param name="i">判斷是否較小的元素。</param>
/// <param name="j">判斷是否較大的元素。</param>
/// <returns></returns>
private bool Less(int i, int j)
=> this.pq[i].CompareTo(this.pq[j]) < 0;
/// <summary>
/// 交換堆中的兩個元素。
/// </summary>
/// <param name="i">要交換的第一個元素下標。</param>
/// <param name="j">要交換的第二個元素下標。</param>
private void Exch(int i, int j)
{
Key swap = this.pq[i];
this.pq[i] = this.pq[j];
this.pq[j] = swap;
}
/// <summary>
/// 檢查當前二叉樹是不是一個最大堆。
/// </summary>
/// <returns></returns>
private bool IsMaxHeap() => IsMaxHeap(1);
/// <summary>
/// 確定以 k 為根節點的二叉樹是不是一個最大堆。
/// </summary>
/// <param name="k">需要檢查的二叉樹根節點。</param>
/// <returns></returns>
private bool IsMaxHeap(int k)
{
if (k > this.n)
return true;
int left = 2 * k;
int right = 2 * k + 1;
if (left <= this.n && Less(k, left))
return false;
if (right <= this.n && Less(k, right))
return false;
return IsMaxHeap(left) && IsMaxHeap(right);
}
}
}
另請參閱
2.4.7
題目
在堆中,最大的元素一定在位置 1 上,第二大的元素一定在位置 2 或者 3 上。
對於一個大小為 31 的堆,
給出第 k 大的元素可能出現的位置和不可能出現的位置,
其中 k=2、3、4(設元素值不重覆)。
解答
k = 2 時,
只可能出現在位置 2、3 上(根節點的子結點,深度為 2,根節點深度為 1)
k = 3 時,
可以直接是根節點的子結點(第 2 或第 3 位,深度為 2),
也可以是第二大元素的子結點(第 4~7 位,也就是深度為 3 的所有位置)
k = 4 時,
可以直接是根節點的子結點(深度為 2 的點)
也可以是第二大元素的子結點(深度為 3 的點)
也可以是第三大元素的子結點(深度為 4 的點)
故範圍為第 2~15 位。
不難看出第 k 大元素只可能出現在深度<k 的位置(\(k \ge 2\))
即位置小於 \(2 ^ k - 1, (k \ge 2)\)
2.4.8
題目
回答上一道練習中第 k 小元素的可能和不可能的位置。
解答
不難看出第 k 大元素只可能出現在深度<k 的位置(\(k \ge 2\))
即位置小於 \(2^k - 1, (k \ge 2)\)。
出現範圍為 \([2, \min \{2^k -1, n\}]\),其中 n 為堆的大小。
2.4.9
題目
給出 A B C D E 五個元素可能構造出來的所有堆,
然後給出 A A A B B 這五個元素可能構造出來的所有堆。
解答
首先 A B C D E 中,根節點必須是 E (假設為最大堆)
D 只能選擇 E 作為父結點。
C 可以選擇 D 或者 E 作為父結點。
B 可以選擇 C 或 D 或 E 作為父結點。
A 可以選擇 B 或 C 或 D 或 E 作為父結點。
又由於堆的大小為 5,堆的結構固定,一共三層。
E 只能為根節點
D 可以在左側或者右側
當 D 在左側時,
D 的子結點可以在 A B C 中任取兩個,剩下一個當 E 的右側子結點
總共有 A(3, 2) = 6 種
當 D 在右側時,
C 的子結點只能取 A 和 B ,故只有 A(2, 2) = 2 種情況。
綜上,最大堆總共有 6 + 2 = 8 種構造堆的方式。
最小堆的構造同理,也有 8 種構造方式。
故總共有 8 + 8 = 16 種構造方式。
構造方式(最大堆):
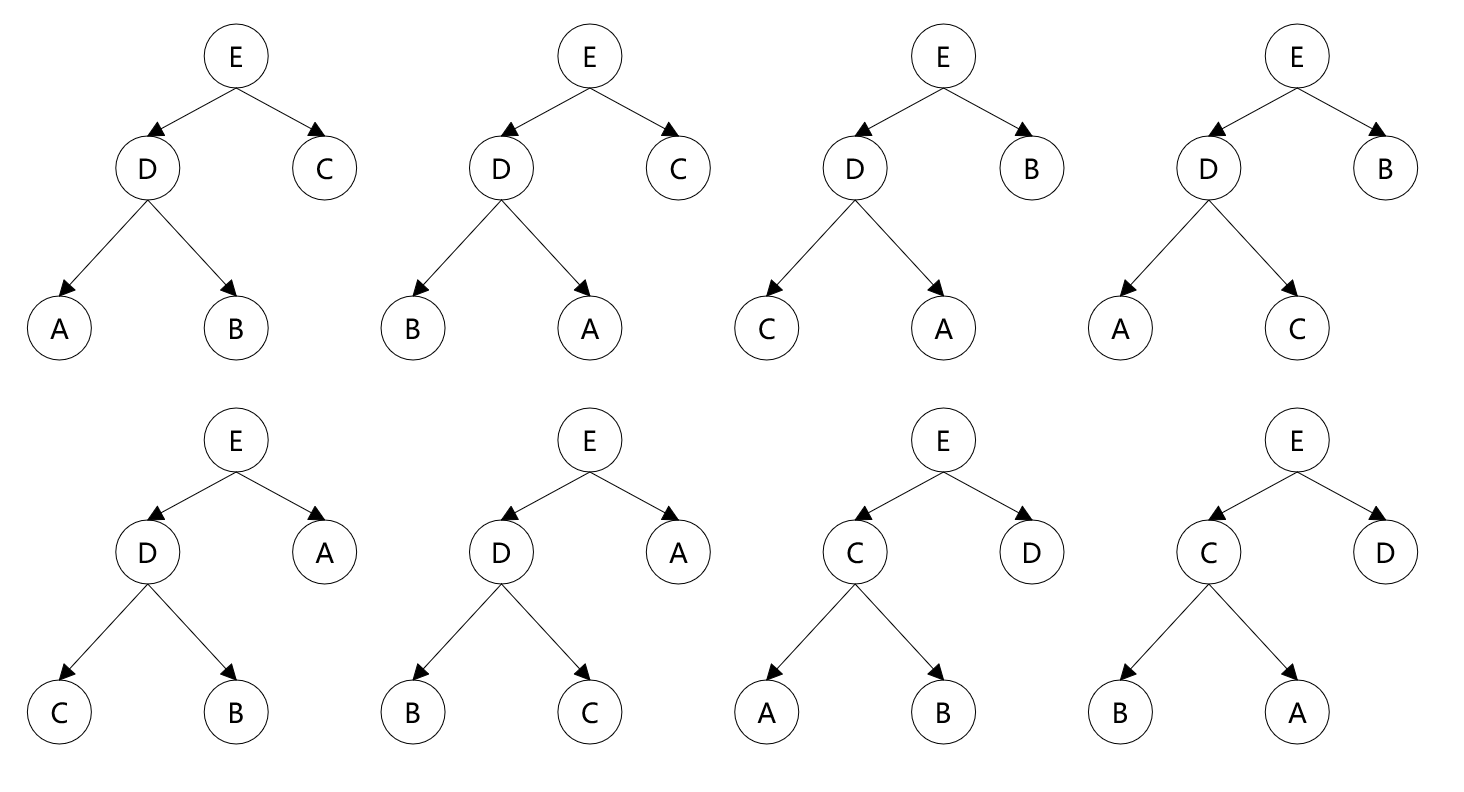
最大堆
B 只能作為 B 的子結點,A 可以是 B 或 A 的子結點。
根節點恆為 B
第二層結點有兩種選擇 A B 和 B A
第三層只有一種選擇 A A
故總共有兩種構造堆的方式。
最小堆
根節點恆為 A
第二層可以是 A A 或 A B
第二層是 A A 時
第三層只能選擇 B B
第二層時 A B 時
第三層可選擇 A B 或 B A
故總共有三種構造堆的方式。
綜上所述,總共有 2 + 3 = 5 種構造方式。
構造方式(全部):
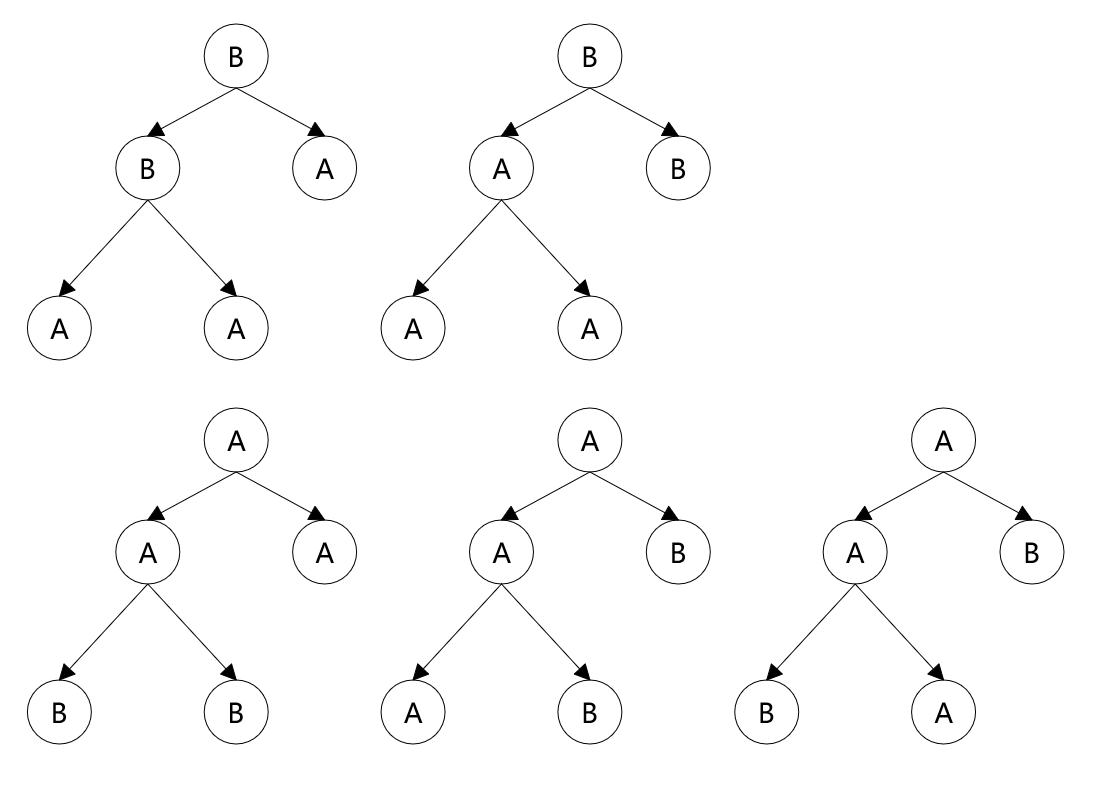
2.4.10
題目
假設我們不想浪費堆排序的數組 pq[] 中的那個位置,
將最大元素放在 pq[0],它的子結點放在 pq[1] 和 pq[2],以此類推。
pq[k] 的父結點和子結點在哪裡?
解答
左子樹位於 \(2k+1\),右子樹位於 \(2k+2\),父結點位於 \(\lfloor (i-1)/2 \rfloor\) 。
2.4.11
題目
如果你的應用中有大量插入元素的操作,但只有若幹刪除最大元素的操作,
哪種優先隊列的實現方法更有效:堆、無序數組、有序數組?
解答
有大量插入操作,選擇插入操作為常數級別的無序數組實現較為合適。
2.4.12
題目
如果你的應用場景中大量的找出最大元素的操作,但插入元素和刪除最大元素操作相對較少,
哪種優先隊列的實現方法更有效:堆、無序數組、有序數組?
解答
有序數組,查找最大元素操作是 O(1) 的。
堆要看具體實現,基於數組的實現和有序數組類似,
在插入操作較多的情況下甚至會優於有序數組。
註:
官網給出的堆實現會在插入/刪除操作之後對整個數組進行檢查,
確認是否為最大堆(isMaxHeap 方法)。
在測試時務必刪除這部分代碼。
2.4.13
題目
想辦法在 sink() 中避免檢查 j<N。
解答
在官方實現的基礎上直接刪除 j<N 語句,隨後在 DelMax() 方法中在 sink(1) 之前讓 pq[n + 1] = pq[1] 即可。
首先保存最大值,然後把堆中的第一個元素和最後一個元素交換,隨後使 n = n - 1。
隨後讓 pq[n + 1] = pq[1],這樣在下沉操作時就不會下沉到 pq[n + 1]了。(相等的元素是不會交換的)
故之後的 Sink() 語句中不再需要進行邊界判斷,直接刪去即可。
修改後 DelMax() 的代碼如下:
public Key DelMax()
{
if (IsEmpty())
throw new ArgumentOutOfRangeException("Priority Queue Underflow");
Key max = this.pq[1];
Exch(1, this.n--);
pq[n + 1] = pq[1];
Sink(1);
this.pq[this.n + 1] = default(Key);
if ((this.n > 0) && (this.n == this.pq.Length / 4))
Resize(this.pq.Length / 2);
Debug.Assert(IsMaxHeap());
return max;
}2.4.14
題目
對於沒有重覆元素的大小為 N 的堆,一次刪除最大元素的操作中最少要交換幾個元素?
構造一個能夠達到這個交換次數的大小為 15 的堆。
連續兩次刪除最大元素呢?三次呢?
解答
對於 n <= 2 的堆
第一步讓最大元素和末端元素交換。
第二步下沉時由於 n <= 1,不需要交換。
故總共發生了一次交換,兩個元素髮生了交換。
對於 n = 3 的堆
第一步讓最大元素和末端元素交換。
第二步如果末端元素大於另一側的子結點,那麼就不需要交換。
故最優情況時總共發生一次交換,兩個元素被交換。
對於 n > 3 的堆。
第一步需要讓最末端元素和最大元素交換。
由於堆中第二大的元素必定位於根節點之後。
故最末端元素一定小於該第二大元素。
因此在下沉操作時必定會和第二大元素進行交換。
故至少發生兩次交換,總共有三個元素髮生了交換。
構造的堆(n=15)
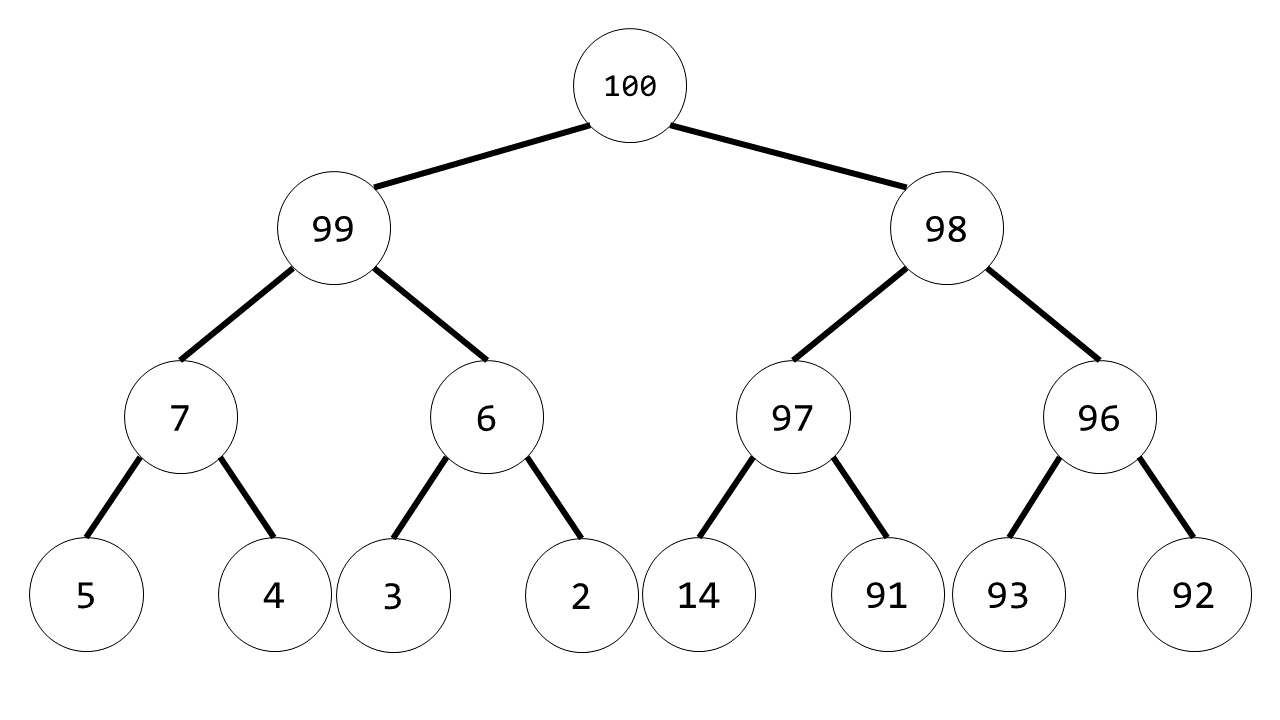
92 和 100 交換,隨後 92 和 99 交換
構造最優情況堆的方式如下(取根結點為 100):
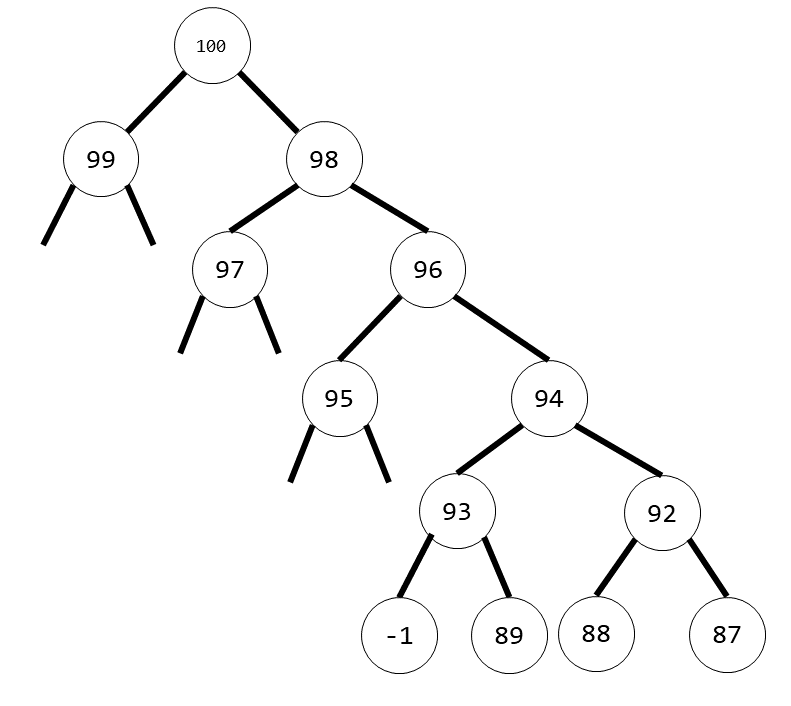
對於每個結點,左子結點大於右子結點,
且左子結點的子元素都小於右子樹的最小值,
(上例中省略了這部分元素,可以將它們當作負數)
於是第一次 DelMax 的時候,只需要兩次交換,三個元素被交換。
(即 87 最後被交換到上例中 99 的位置)
第二次 DelMax 的時候,只需要三次交換,六個元素被交換.
(88 交換到 97 的位置)
因此當 n > 7 時,連續兩次 DelMax() 最少只需要 5 次交換。
第三次 DelMax 的時候,只需要四次交換,九個元素被交換。
(89 交換到 95 的位置)
因此當 n > 15 時,連續三次 DelMax() 最少只需要 9 次交換。
2.4.15
題目
設計一個程式,線上性時間內檢測數組 pq[] 是否是一個面向最小元素的堆。
解答
MinPQ 的官方實現見:https://algs4.cs.princeton.edu/24pq/MinPQ.java.html
事實上只需要把 MaxPQ 中的比較調換方向即可。
線上性時間內檢測是否是面向最小元素的堆的方法:
/// <summary>
/// 確定以 k 為根節點的二叉樹是不是一個最小堆。
/// </summary>
/// <param name="k">需要檢查的二叉樹根節點。</param>
/// <returns></returns>
private bool IsMinHeap(int k)
{
if (k > this.n)
return true;
int left = 2 * k;
int right = 2 * k + 1;
if (left <= this.n && Greater(k, left))
return false;
if (right <= this.n && Greater(k, right))
return false;
return IsMinHeap(left) && IsMinHeap(right);
}用遞歸方法遍歷整個二叉樹,確認都滿足堆的性質。由於每個結點都只會被比較三次(與父結點比較一次,與每個子結點各比較一次),由於 3N~N,因此這個方法是 O(n) 的。
代碼
最小堆的介面 IMinPQ。
using System;
namespace PriorityQueue
{
/// <summary>
/// 實現優先隊列 API 的介面。(最小堆)
/// </summary>
/// <typeparam name="Key">優先隊列容納的元素。</typeparam>
public interface IMinPQ<Key> where Key : IComparable<Key>
{
/// <summary>
/// 向優先隊列中插入一個元素。
/// </summary>
/// <param name="v">插入元素的類型。</param>
void Insert(Key v);
/// <summary>
/// 返回最小元素。
/// </summary>
/// <returns></returns>
Key Min();
/// <summary>
/// 刪除並返回最小元素。
/// </summary>
/// <returns></returns>
Key DelMin();
/// <summary>
/// 返回隊列是否為空。
/// </summary>
/// <returns></returns>
bool IsEmpty();
/// <summary>
/// 返回隊列中的元素個數。
/// </summary>
/// <returns></returns>
int Size();
}
}MinPQ.cs
using System;
using System.Collections;
using System.Collections.Generic;
using System.Diagnostics;
namespace PriorityQueue
{
/// <summary>
/// 最小堆。(數組實現)
/// </summary>
/// <typeparam name="Key">最小堆中保存的元素類型。</typeparam>
public class MinPQ<Key> : IMinPQ<Key>, IEnumerable<Key> where Key : IComparable<Key>
{
private Key[] pq; // 保存元素的數組。
private int n; // 堆中的元素數量。
/// <summary>
/// 預設構造函數。
/// </summary>
public MinPQ() : this(1) { }
/// <summary>
/// 建立指定容量的最小堆。
/// </summary>
/// <param name="capacity">最小堆的容量。</param>
public MinPQ(int capacity)
{
this.pq = new Key[capacity + 1];
this.n = 0;
}
/// <summary>
/// 從已有元素建立一個最小堆。(O(n))
/// </summary>
/// <param name="keys">已有元素。</param>
public MinPQ(Key[] keys)
{
this.n = keys.Length;
this.pq = new Key[keys.Length + 1];
for (int i = 0; i < keys.Length; i++)
this.pq[i + 1] = keys[i];
for (int k = this.n / 2; k >= 1; k--)
Sink(k);
Debug.Assert(IsMinHeap());
}
/// <summary>
/// 刪除並返回最小元素。
/// </summary>
/// <returns></returns>
public Key DelMin()
{
if (IsEmpty())
throw new ArgumentOutOfRangeException("Priority Queue Underflow");
Key min = this.pq[1];
Exch(1, this.n--);
this.pq[this.n + 1] = this.pq[1];
Sink(1);
this.pq[this.n + 1] = default(Key);
if ((this.n > 0) && (this.n == this.pq.Length / 4))
Resize(this.pq.Length / 2);
//Debug.Assert(IsMinHeap());
return min;
}
/// <summary>
/// 向堆中插入一個元素。
/// </summary>
/// <param name="v">需要插入的元素。</param>
public void Insert(Key v)
{
if (this.n == this.pq.Length - 1)
Resize(2 * this.pq.Length);
this.pq[++this.n] = v;
Swim(this.n);
//Debug.Assert(IsMinHeap());
}
/// <summary>
/// 檢查堆是否為空。
/// </summary>
/// <returns></returns>
public bool IsEmpty() => this.n == 0;
/// <summary>
/// 獲得堆中最小元素。
/// </summary>
/// <returns></returns>
public Key Min() => this.pq[1];
/// <summary>
/// 獲得堆中元素的數量。
/// </summary>
/// <returns></returns>
public int Size() => this.n;
/// <summary>
/// 獲取堆的迭代器,元素以降序排列。
/// </summary>
/// <returns></returns>
public IEnumerator<Key> GetEnumerator()
{
MaxPQ<Key> copy = new MaxPQ<Key>(this.n);
for (int i = 1; i <= this.n; i++)
copy.Insert(this.pq[i]);
while (!copy.IsEmpty())
yield return copy.DelMax(); // 下次迭代的時候從這裡繼續執行。
}
/// <summary>
/// 獲取堆的迭代器,元素以降序排列。
/// </summary>
/// <returns></returns>
IEnumerator IEnumerable.GetEnumerator()
{
return GetEnumerator();
}
/// <summary>
/// 使元素上浮。
/// </summary>
/// <param name="k">需要上浮的元素。</param>
private void Swim(int k)
{
while (k > 1 && Greater(k / 2, k))
{
Exch(k, k / 2);
k /= 2;
}
}
/// <summary>
/// 使元素下沉。
/// </summary>
/// <param name="k">需要下沉的元素。</param>
private void Sink(int k)
{
while (k * 2 <= this.n)
{
int j = 2 * k;
if (Greater(j, j + 1))
j++;
if (!Greater(k, j))
break;
Exch(k, j);
k = j;
}
}
/// <summary>
/// 重新調整堆的大小。
/// </summary>
/// <param name="capacity">調整後的堆大小。</param>
private void Resize(int capacity)
{
Key[] temp = new Key[capacity];
for (int i = 1; i <= this.n; i++)
{
temp[i] = this.pq[i];
}
this.pq = temp;
}
/// <summary>
/// 判斷堆中某個元素是否大於另一元素。
/// </summary>
/// <param name="i">判斷是否較大的元素。</param>
/// <param name="j">判斷是否較小的元素。</param>
/// <returns></returns>
private bool Greater(int i, int j)
=> this.pq[i].CompareTo(this.pq[j]) > 0;
/// <summary>
/// 交換堆中的兩個元素。
/// </summary>
/// <param name="i">要交換的第一個元素下標。</param>
/// <param name="j">要交換的第二個元素下標。</param>
private void Exch(int i, int j)
{
Key swap = this.pq[i];
this.pq[i] = this.pq[j];
this.pq[j] = swap;
}
/// <summary>
/// 檢查當前二叉樹是不是一個最小堆。
/// </summary>
/// <returns></returns>
private bool IsMinHeap() => IsMinHeap(1);
/// <summary>
/// 確定以 k 為根節點的二叉樹是不是一個最小堆。
/// </summary>
/// <param name="k">需要檢查的二叉樹根節點。</param>
/// <returns></returns>
private bool IsMinHeap(int k)
{
if (k > this.n)
return true;
int left = 2 * k;
int right = 2 * k + 1;
if (left <= this.n && Greater(k, left))
return false;
if (right <= this.n && Greater(k, right))
return false;
return IsMinHeap(left) && IsMinHeap(right);
}
}
}另請參閱
2.4.16
題目
對於 N=32,構造數組使得堆排序使用的比較次數最多以及最少。
解答
最好情況比較簡單,只需要一個所有鍵值完全相同的數組即可。
最壞情況的構造方法參考了一篇論文(見「另請參閱」部分),結果如下:

最好輸入:
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
最壞輸入:
1 4 7 12 10 16 14 19 17 20 5 27 8 28 2 24 9 18 6 23 11 22 21 31 13 26 25 30 15 29 3 32
代碼
用於構造堆排序最壞情況的類。
using System;
using System.Collections;
using System.Collections.Generic;
using System.Diagnostics;
namespace PriorityQueue
{
/// <summary>
/// 生成最大堆的最壞情況。參考論文:https://arxiv.org/abs/1504.01459
/// </summary>
public class MaxPQWorstCase
{
private int[] pq; // 保存元素的數組。
private int n; // 堆中的元素數量。
/// <summary>
/// 建立指定容量的最大堆。
/// </summary>
/// <param name="capacity">最大堆的容量。</param>
public MaxPQWorstCase(int capacity)
{
this.pq = new int[capacity + 1];
this.n = 0;
}
/// <summary>
/// 製造堆排序的最壞情況。
/// </summary>
/// <param name="n">需要構造的數組大小。</param>
/// <returns>最壞情況的輸入數組。</returns>
public int[] MakeWorst(int n)
{
int[] strategy = Win(n);
for (int i = 0; i < strategy.Length; i++)
{
UnRemoveMax(strategy[i]);
}
for (int i = 1; i <= this.n / 2; i++)
UnFixHeap(i);
int[] worstCase = new int[n];
for (int i = 1; i <= n; i++)
worstCase[i - 1] = this.pq[i];
return worstCase;
}
private bool Less(int i, int j) => this.pq[i].CompareTo(this.pq[j]) < 0;
private int PullDown(int i, int j)
{
int toReturn = this.pq[j];
for (int m = j; m / 2 >= i; m /= 2)
{
this.pq[m] = this.pq[m / 2];
}
return toReturn;
}
private void UnFixHeap(int i)
{
int j = (int)(i * Math.Pow(2, Math.Floor(Math.Log10(this.n / i) / Math.Log10(2))));
this.pq[i] = PullDown(i, j);
}
private void UnRemoveMax(int i)
{
int p = (this.n + 1) / 2;
if (Less(p, i))
return;
this.n++;
this.pq[this.n] = PullDown(1, i);
this.pq[1] = this.n;
}
private int[] Par(int l)
{
int n = (int)Math.Pow(2, l) - 1;
int[] s7 = { 0, 1, 2, 3, 4, 4, 5 };
int[] strategy = new int[n];
for (int i = 0; i < Math.Min(n, 7); i++)
{
strategy[i] = s7[i];
}
if (n <= 7)
return strategy;
for (int lev = 3; lev < l; lev++)
{
int i = (int)Math.Pow(2, lev) - 1;
strategy[i] = i;
strategy[i + 1] = i - 1;
strategy[i + 2] = i + 1;
strategy[i + 3] = i + 2;
strategy[i + 4] = i + 4;
strategy[i + 5] = i + 3;
for (int k = i + 6; k <= 2 * i; k++)
{
strategy[k] = k - 1;
}
}
return strategy;
}
private int[] Win(int n)
{
int[] strategy = new int[n];
int[] s = Par((int)Math.Floor(Math.Log10(n) / Math.Log10(2)) + 1);
for (int i = 1; i <= n - 1; i++)
{
strategy[i] = s[i];
}
int I = (int)Math.Pow(2, Math.Floor(Math.Log10(n + 1) / Math.Log10(2))) - 1;
if ((n == I) || (n <= 7))
return strategy;
strategy[I] = I;
if (n == I + 1)
return strategy;
strategy[I + 1] = (I + 1) / 2;
if (n == I + 2)
return strategy;
for (int i = I + 2; i <= n - 1; i++)
{
if (i == 2 * I - 2)
strategy[i] = i;
else
strategy[i] = i - 1;
}
return strategy;
}
}
}另請參閱
給出堆排序最壞情況構造方法的論文
Suchenek M A. A Complete Worst-Case Analysis of Heapsort with Experimental Verification of Its Results, A manuscript (MS)[J]. arXiv preprint arXiv:1504.01459, 2015.
本題用到的庫文件
PriorityQueue 庫
2.4.17
題目
證明:構造大小為 k 的面向對象最小元素的優先隊列,
然後進行 N-k 次替換最小元素操作(刪除最小元素後再插入元素)後,
N 個元素中的前 k 大元素均會留在優先隊列中。
解答
英文版原文是:insert followed by remove the minimum,因此是先插入再刪除。
大致上相當於一個緩衝區,把比較大的留下來,比較小的篩出去。
首先我們有一個大小為 k 的優先隊列,保證最小值在最前。
接下來我們插入一個元素,可以分成兩種情況。
如果插入的元素比最小值還要小,那麼這個插入的元素會在之後被刪除,原隊列中的元素不變。
如果插入的元素比最小值大(或者相等),那麼最小值會被刪除,留下插入的元素。
於是可以觀察到這樣一個邏輯,在不斷的插入過程中,比較小的元素會被過濾,只留下較大的元素。
那麼我們可以把題目轉化為:
向一個優先隊列插入 N 個元素,保證隊列的大小不超過 k,如果超過 k 了就刪除最小值。
那麼前 k 次插入不受影響,之後的 N-k 次插入就會按照之前說過的流程進行。
最後只留下 N 個元素中較大的 k 個元素,得證。
2.4.18
題目
在 MaxPQ 中,如果一個用例使用 insert() 插入了一個比隊列中的所有元素都大的新元素,隨後立即調用 delMax()。
假設沒有重覆元素,此時的堆和進行這些操作之前的堆完全相同嗎?
進行兩次 insert()
(第一次插入一個比隊列所有元素都大的元素,第二次插入一個更大的元素)
操作接兩次 delMax() 操作呢?
解答
首先看第一種情況,一次 insert() 接一次 delMax()。
由於插入的數比堆中的所有元素都大,這個元素會一路上升到根結點。
記上升路徑上的點為 $ a_1,a_2,a_3, \dots , a_k $,其中 $ a_k $ 是插入的結點,$ a_1 $ 是根結點。
插入完成後路徑上點的次序變為 $ a_k, a_1, a_2, \dots, a_{k-1} $ 。
隨後進行一次 delMax(),先做交換,次序變為 $ a_{k-1}, a_1, \dots, a_{k-2}, a_k $ 。
由於 $ a_1 $ 是堆中原來的最大值,下沉時一定會和它交換。
根據定義,二叉堆是父結點總是優於子結點的完全二叉樹,因此以後續結點作為根結點的子樹也都是堆。
故同理 $ a_{k-1} $ 會和 $ a_2, a_3, \dots,a_{k-2} $ 交換,即沿原路徑返回。
因此這種情況下前後堆不發生改變。
然後看第二種情況,操作順序為 insert() insert() delMax() delMax()。
根據之前的結論,插入最大結點之後立即刪除最大元素不會使堆發生變化,中間的兩個操作抵消。
序列變為:insert() delMax()。
同理再次利用剛纔的結論,操作抵消,堆不發生變化。
故第二種情況也不會使堆發生改變。
2.4.19
題目
實現 MaxPQ 的一個構造函數,接受一個數組作為參數。
使用正文 2.4.5.1 節中所述的自底向上的方法構造堆。
解答
官方實現已經包含了這部分的代碼,見:https://algs4.cs.princeton.edu/24pq/MaxPQ.java.html
相應的構造函數(Java)
public MaxPQ(Key[] keys) {
n = keys.length;
pq = (Key[]) new Object[keys.length + 1];
for (int i = 0; i < n; i++)
pq[i+1] = keys[i];
for (int k = n/2; k >= 1; k--)
sink(k);
assert isMaxHeap();
}代碼
構造函數(C#)
/// <summary>
/// 從已有元素建立一個最大堆。(O(n))
/// </summary>
/// <param name="keys">已有元素。</param>
public MaxPQ(Key[] keys)
{
this.n = keys.Length;
this.pq = new Key[keys.Length + 1];
for (int i = 0; i < keys.Length; i++)
this.pq[i + 1] = keys[i];
for (int k = this.n / 2; k >= 1; k--)
Sink(k);
Debug.Assert(IsMaxHeap());
}另請參閱
2.4.20
題目
證明:基於下沉的堆構造方法使用的比較次數小於 2N,交換次數小於 N。
解答
官網給出瞭解答:https://algs4.cs.princeton.edu/24pq/
首先介紹第一種解法。
設葉子結點的高度為 $ 0 $,根結點的高度為 $ h $。
於是某個結點 sink 時的最大交換次數即為該結點的高度。
故某一層結點的最大交換次數為 該層結點數 × 該層的高度。
於是總交換次數最大為:
\[
\begin{align*}
& h+2(h-1)+2^2(h-2)+ \dots + 2^h(0) \\
& =\sum_{k=0}^{h-1} 2^k(h-k) \\
& =h\sum_{k=0}^{h-1}2^k - \sum_{k=0}^{h-1}k2^k \\
\end {align*}
\]
第一項為等比數列的和,第二項為等差數列乘以等比數列的和。
於是第一項可以直接通過公式求得,第二項可以利用錯位相減法求得。
\[
\begin{align*}
& h\sum_{k=0}^{h-1}2^k - \sum_{k=0}^{h-1}k2^k \\
& =h2^{h}-h-\sum_{k=0}^{h-1}k2^k \\
& =h2^{h}-h +\sum_{k=0}^{h-1} k2^k - 2\sum_{k=0}^{h-1} k2^k \\
& =h2^{h}-h+2^h - 2-(h-1)2^h \\
& =2^{h+1}-h-2 \\
& =N-h-1 \le N
\end{align*}
\]
於是交換次數小於 $ N $,比較次數小於 $ 2N $。
另一種解法,可以配合官網的圖片幫助理解。
首先堆中某個結點最多一路下沉到葉子結點,
最大交換次數就是該結點的高度(記葉子結點的高度為 0)。
考慮根結點一路下沉到葉子結點的軌跡,
設為 $ a_0, a_1, a_2, ... , a_k $,其中 $ k $ 為根結點的高度,$ a_0 $ 是根結點。
$ a_0 $ 下沉後結點順序變為 $ a_1, a_2, ..., a_k, a_0 $ 。
根據下沉的定義,有 $ a_1 > a_2 > \dots > a_k > a_0 $ 。
因此 $ a_1 $ 下沉時不可能與 $ a_2 $ 交換,而會向另一個方向下沉。
其餘結點同理,可以發現每個結點的下沉路徑不會與其他結點重合。
一棵完全二叉樹共有 $ N - 1 $ 條邊,每訪問一條邊代表進行了一次交換。
故交換次數必定小於 $ N $,比較次數為交換次數的兩倍小於 $ 2N $。
2.4.21
題目
基礎數據結構。
說明如何使用優先隊列實現第一章中的棧、隊列和隨機隊列這幾種數據結構。
解答
給元素添上序號組成結點,按照序號排序即可,每個結點可以用類似於這樣的實現:
class ElemType<T> : IComparable<ElemType<T>>
{
private int key;
private T element;
public ElemType(int key) => this.key = key;
public int CompareTo(ElemType<T> other)
{
return this.key.CompareTo(other.key);
}
}棧:
用最大元素在最前的優先隊列。
每個結點都包含一個元素和一個序號,
插入新元素時序號遞增,這樣最後插入的元素總在最前。
隊列:
用最小元素在最前的優先隊列。
每個結點都包含一個元素和一個序號,
插入新元素時序號遞增,這樣最先插入的元素總在最前。
隨機隊列:
優先隊列的選擇任意
每個結點都包含一個元素和一個序號,
插入新元素時隨機指定一個序號,這樣元素的順序就是任意的了。
2.4.22
題目
調整數組大小。
在 MaxPQ 中加入調整數組大小的代碼,
並和命題 Q 一樣證明對於一般性長度為 N 的隊列其數組訪問的上限。
解答
官方實現中已經包含了調整數組大小的代碼,見:https://algs4.cs.princeton.edu/24pq/MaxPQ.java.html
截取如下:
// helper function to double the size of the heap array
private void resize(int capacity) {
assert capacity > n;
Key[] temp = (Key[]) new Object[capacity];
for (int i = 1; i <= n; i++) {
temp[i] = pq[i];
}
pq = temp;
}只要在隊列快滿時重新分配空間,再把元素複製進去即可。
在不觸發重新分配空間的情況下,
每次隊列操作的比較次數上限就等於命題 Q 中給出的 $ \lg N+1 $(插入) 和 $ 2\lg N $(刪除)。
插入元素最多需要 $ \lg N $ 次交換(比較次數-1),
刪除元素最多需要 \(1 + \lg N - 1 = \lg N\) 次交換 (註意開始時有一次交換)。
同時一次比較需要 $ 2 $ 次數組訪問,一次交換需要 \(4\) 次數組訪問(記 a[i] 為一次數組訪問)。
換算成數組訪問次數就是 $ 6 \lg N + 2 $(插入)和 $ 8 \lg N $ (刪除)。
在觸發重新分配空間的情況下,需要額外的 $ 2N $ 次數組訪問來重新分配空間。
故上限為 $ 6 \lg N +2N + 2 $ 和 $ 8 \lg N + 2N $。
如果取均攤分析,那麼相當於把多出來的 $ 2N $ 次訪問平均到 $ N $ 次操作中。
設第 $ n $ 次插入觸發了重新分配空間,$ n $ 是 $ 2 $ 的冪。
重新分配空間進行了 $ 2 + 4 + 8 + 16 + ... + 2n = 2n - 2 $ 次數組訪問。
平均到 $ n $ 次插入過程,每次插入多進行 $ 2 - 2 / n $ 次數組訪問。
於是插入的上限變為 $ 6 \lg N + 4 - 2 / N $。
同理刪除的上限變為 $ 8 \lg N + 2 - 2 / N $。
代碼
重新分配空間(C#)
/// <summary>
/// 重新調整堆的大小。
/// </summary>
/// <param name="capacity">調整後的堆大小。</param>
private void Resize(int capacity)
{
Key[] temp = new Key[capacity];
for (int i = 1; i <= this.n; i++)
{
temp[i] = this.pq[i];
}
this.pq = temp;
}另請參閱
2.4.23
題目
Multiway 的堆。
只考慮比較的成本且假設找到 t 個元素中的最大者需要 t 次比較,
在堆排序中使用 t 向堆的情況下找出使比較次數 NlogN 的繫數最小的 t 值。
首先,假設使用的是一個簡單通用的 sink() 方法;
其次,假設 Floyd 方法在內迴圈中每輪可以節省一次比較。
解答
簡單的 sink 實現
sink 方法會在所有的 $ t $ 個子結點中尋找最大的結點。
如果找到的結點比當前結點大,那麼就進行交換。
否則視為結點已經下沉到了合適的位置,結束迴圈。
根據題意,在 $ t $ 個元素中找最大值需要 $ t $ 次比較。
sink 操作需要找到 $ t $ 個子結點中的最大值並與當前結點相比較。
於是 sink 操作每次最多需要 $ t + 1 $ 次比較。
建堆過程,對 2.4.20 的證明進行推廣。
設 $ t $ 叉樹的高度為 $ h $ ,葉子結點的高度為 $ 0 $,根結點的高度為 $ h $。
根據 sink 操作的定義,高度為 $ k $ 的結點最多進行 $ k $ 次交換(到達葉子結點)。
於是建堆需要的總交換次數為:
\[
\begin{align*}
& h+t(h-1)+t^2(h-2)+ \dots + t^h(0) \\
& =\sum_{k=0}^{h-1} t^k(h-k) \\
& =h\sum_{k=0}^{h-1}t^k - \sum_{k=0}^{h-1}kt^k \\
\end {align*}
\]
其中,第一個數列是等比數列,第二個數列是等差數列和等比數列之積,可以利用錯位相減法求得,即:
\[
\begin{align*}
& h\sum_{k=0}^{h-1}t^k - \sum_{k=0}^{h-1}kt^k \\
& =\frac{h-ht^{h}}{1-t}-\sum_{k=0}^{h-1}kt^k \\
& =\frac{h-ht^{h}}{1-t} -\frac{\sum kt^k - t\sum kt^k}{1-t} \\
& =\frac{h-ht^h}{1-t}-\frac{t(1-t^{h-1})}{(1-t)^2}+\frac{(h-1)t^h}{1-t} \\
& =\frac{h-t^h}{1-t}-\frac{t(1-t^{h-1})}{(1-t)^2} \\
& =\frac{h-ht+t^{h+1}-t}{(1-t)^2}
\end{align*}
\]
考慮到對於 $ t $ 叉堆,結點數可以表示為 $ n=\frac{t^{h+1}-1}{t-1} $ 。故交換次數可以化簡為:
\[
\begin{align*}
& \frac{h-ht+t^{h+1}-t}{(1-t)^2} \\
& =\frac{h-ht+t^{h+1}-t +1-1}{(1-t)^2} \\
& =\frac{t^{h+1}-1}{(1-t)^2}+\frac{h-ht-t+1}{(1-t)^2} \\
& =-\frac{n}{1-t}+\frac{h}{1-t}+\frac{1}{1-t} \\
& =\frac{n-h-1}{t-1} \le n
\end{align*}
\]
故建堆所需比較次數最大為 $ (t+1)n $。
每次刪除最大元素都會對根結點調用一次 sink 操作,
因此排序所需的比較次數最多為 $ (t+1)n\log_t(n) $。
相加得堆排序所需的總交換次數最多為 $ (t+1)n + (t+1)n\log_t(n) =(t+1)(n\log_tn+n) $ 。
利用換底公式將對數的底換成 2,得到:$ \frac{t+1}{\lg t} n\log n $。
於是問題變為求 $ f(t)= \frac{t+1}{\lg t} $ 的最小值,對其求導,得到:
\[
( \frac{t+1}{\lg t} )'=\frac{-t+t\ln t-1}{t\ln^2t}·\ln 2
\]
直接求導數的零點會比較困難,但利用勘根公式可以尋找到根所在的區間。
由於 \(\ln 2\) 不影響正負,我們直接將其去掉,變為
\[
\frac{-t+t\ln t-1}{t\ln^2t}=\frac{-1+\ln t-\frac{1}{t}}{\ln^2t}
\]
由於 $ t > 1 $,分母總是為正,因此導函數正負就等於下麵這個函數的正負:
\[
\begin {align*}
g(t)=\ln t -1-\frac{1}{t}
\end {align*}
\]
$ t = e $ 時 $ g(t) < 0 $ ,$ t=e+1 $ 時 $ g(t) > 0 $。於是可以求得在 $ (e, e+1) $ 上 $ f(t) $ 存在極小值。
又由於 $ g(t) $ 在 $ (e + 1, +\infty) $ 始終為正,因此在 $ (e, e+1) $ 上存在的是最小值($ t \ge 2 $)。
因為 $ t $ 為大於 $ 1 $ 的正整數,且 $ f(4) < f(3) $,故 $ t=4 $ 時繫數最小,此時繫數為 $ 2.5 $。
Floyd 方法
在刪除最大元素的過程中,根結點會和最後一個結點交換,然後對新的根結點執行 sink 操作。
大多數情況下,這個結點會被一路交換到樹的最後一層。
因此我們省去 sink 操作中與自己比較的過程,直接和子結點中的較大者進行交換。
這樣一路交換到樹的底部,隨後再讓這個結點與自己的父結點比較,向上「回到」合適的位置。
大多數結點都不需要向上交換,
因此這樣的優化可以減少比較次數(下降一層需要的比較次數從 $ t+1 $ 變為 $ t $)。
利用 Floyd 方法對於建堆沒有影響(建堆也可以使用 Floyd 方法,參見「另請參閱」部分)。
於是建堆的比較次數仍為 $ (t+1)n $。
排序的比較次數變為 $ tn\log_t(n) $。
總的比較次數變為 $ (t+1)n + tn\log_t(n) $。
我們仍然只關心 \(n\lg n\) 的繫數,繫數為 $ f(t)= \frac{t}{\lg t} $。
按照之前的方法再求一次最小值,求得 $ t = 3 $ 時繫數最小,此時繫數為 $ 1.89 $。
另請參閱
Floyd 提出的堆排序優化
Floyd R W. Algorithm 245: treesort[J]. Communications of the ACM, 1964, 7(12): 701.
通過將這種方法應用到建堆獲得的快速建堆方法
McDiarmid C J H, Reed B A. Building heaps fast[J]. Journal of algorithms, 1989, 10(3): 352-365.
2.4.24
題目
使用鏈接的優先隊列。
用堆排序的二叉樹實現一個優先隊列,但使用鏈表結構代替數組。
每個結點都需要三個鏈接:兩個向下,一個向上。
你的實現即使在無法預知隊列大小的情況下也能保證優先隊列的基本操作所需時間為對數級別。
解答
鏈式實現,每個結點都包含一個指向父結點的指針和兩個指向子結點的指針。
交換結點可以直接用交換兩個結點的值來實現(與數組的實現一樣),而不是對兩個結點的指針進行交換。
於是 Sink() 和 Swim() 操作就比較簡單,直接按照定義實現即可。
比較困難的是刪除和插入結點,或者更具體的說,
如何找到按照完全二叉樹定義下序號向後/向前一位的結點?
我們首先在堆裡面維護兩個指針,一個指向根結點(root),另一個指向當前最後一個結點(last)。
當需要插入新結點時,我們需要找到 last 的後一位的父結點,然後把新的結點插入為該結點的左子結點。
這段話可能比較繞,下麵這個示意圖可以幫助理解,有三種情況:

標黃的代表 last 指著的位置。
我們先從簡單的說起,中間的第二種情況,新插入的結點應該放在右側,即作為 last 的父結點的右子結點。
如果 last 已經是右子結點了,那麼就考慮第三種情況。
此時應該向上回溯,直到在某一次回溯中,結點是從父結點的左側回溯上來的
(即圖中路徑 A-B-B,B-B 這一步是從左子樹回溯上來的)。
於是待插入的位置就在該父結點的右子樹的最左側結點(即圖中根結點的右子結點 A)。
最後是圖中第一種情況,整棵樹已經是滿二叉樹了。
這種情況下會一路回溯到根結點,那麼只要一路下沉到最左側的葉子結點,把新結點插入到其左子樹上即可。
刪除結點同理,也是這三種情況,只是需要找前一個結點,判斷條件中的左右正好相反。
如果已經是右子結點了,只需要把 last 改為其父結點的左子樹即可。
如果是左子結點,就需要回溯,直到某一次回溯是從右子樹回溯上來的,last 應該指向其左子樹的最右側結點。
如果刪除後正好變成滿二叉樹,那麼會一直回溯到根結點,last 應該指向整棵樹的最右側結點。
代碼實現中還需要處理只有一個結點以及沒有結點時的特殊情況。
根據上面的演算法,插入/刪除找到相應位置所需的最大耗時為 2lgN
(從樹的一側回溯到根結點,再下沉到另一側的底部)。
Sink 和 Swim 是 O(lgN) 級的,因此整個插入/刪除操作是 O(lgN) 的。
代碼
using Sy


