c++ 搜索二叉樹 插入，刪除，遍歷操作

来源:https://www.cnblogs.com/clc2008/archive/2018/12/29/10193550.html
-Advertisement-
Play Games

搜索二叉樹是一種具有良好排序和查找性能的二叉樹數據結構，包括多種操作，本篇只介紹插入，排序（遍歷），和刪除操作，重點是刪除操作比較複雜，用到的例子也是本人親自畫的 用到的測試圖數據例子 第一、構建節點 1 template <typename T> class BST; 2 template <ty ...


搜索二叉樹是一種具有良好排序和查找性能的二叉樹數據結構，包括多種操作，本篇只介紹插入，排序（遍歷），和刪除操作，重點是刪除操作比較複雜，用到的例子也是本人親自畫的

用到的測試圖數據例子

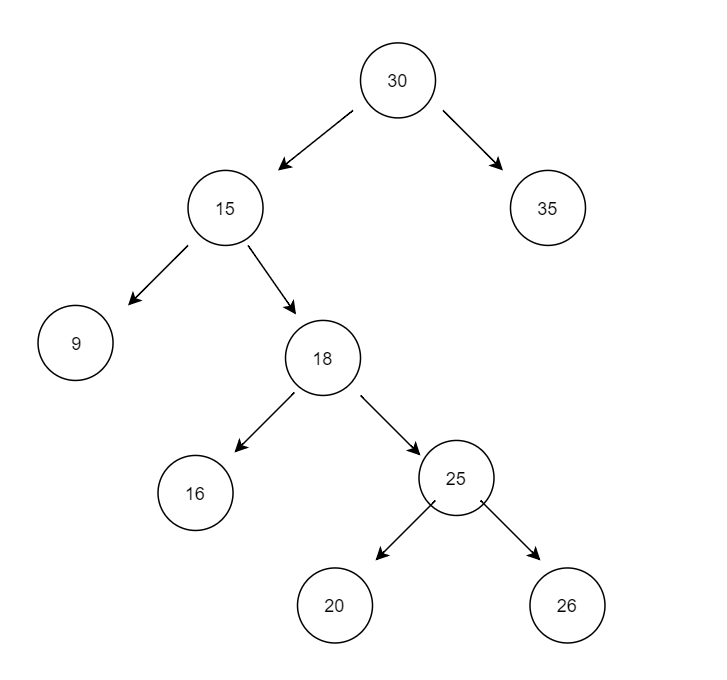
第一、構建節點

 1 template <typename T> class BST;
 2 template <typename T> class BSTNode {
 3 public:
 4     friend class BST<T>;
 5     BSTNode() {
 6         lChild = rChild = parent = NULL;
 7         data = NULL;
 8     }
 9     BSTNode(T d) {
10         lChild = rChild = parent = NULL;
11         data = d;
12     }
13 private:
14     BSTNode<T> *lChild, *rChild, *parent;
15     T data;
16 };
View Code

 

第二、二叉樹頭文件定義

 1 template<typename T> class BST {
 2 public:    
 3     BST() { } 
 4 
 5     //插入操作
 6     void insert(BSTNode<T>*node);
 7 
 8     //二叉查找樹的中序遍歷，就相當於排序了
 9     void inSort(BSTNode<T>*node);
10 
11     //按節點刪除
12     void deleteNode(BSTNode<T>* node);
13 
14     //按數值刪除
15     void deleteNode(const T& t);
16 
17     BSTNode<T>* search(T key);
18     BSTNode<T>* root=NULL;
19 
20 private:    
21     int count;
22 };
View Code

 

第三、搜索二叉樹的插入

1）如果二叉樹查找樹為空節點，則插入節點就為根節點

2）如果二叉查找樹為非空節點，就需要先找到待插入節點，查找原則就是從根節點開始，如果大於根就右邊走，小於根就左邊走，直到找到合適節點，

下麵代碼中的最終找到的temp 就是待插入節點.

 1 template<typename T>
 2 void BST<T>::insert(BSTNode<T>* node)
 3 {
 4     BSTNode<T>* curr, *temp = NULL;
 5     curr = root;
 6     while (NULL!= curr) //遍歷二叉樹，找到應該插入的父節點
 7     {
 8         temp = curr;
 9         if (node->data>curr->data)
10         {
11             curr = curr->rChild;
12         }
13         else {
14             curr = curr->lChild;
15         }
16     }
17     node->parent = temp;//temp 代碼當前最後遍歷的node，設置node->parent為該節點
18     if (temp==NULL)
19     {
20         root = node;
21         count++;
22     }
23     else {
24         if (node->data<temp->data)
25         {
26             temp->lChild = node;
27             count++;
28         }
29         else {
30             temp->rChild = node;
31             count++;
32         }
33     }
34 }
View Code

 

第四、搜索二叉樹的刪除

 刪除包含多種情況，

1. 如果節點沒有子女，修改其父節點指針為NULL，刪除即可

2. 如果該節點有左孩子情況，修改其父親節點的指針和其左孩子的parent指針即可

3. 如果該節點有右孩子情況，修改其父親節點的指針和其右孩子的parent指針即可

4.如果同時有左右孩子的情況，情況比較複雜，一般有2種方法處理

    1） 用節點右邊孩子的最小值替換該節點，其他節點位置保持不變（本篇用這種方法）

    2）用節點左邊孩子的最大值替換該節點，其他節點位置保持不變

後面測試例子是刪除18 node，通過程式找到右邊最小值20，用20 替換18，其他節點位置保持不動。

 

  1 template<typename T>
  2 inline void BST<T>::deleteNode(BSTNode<T>* node)
  3 {
  4     BSTNode<T>*p = node->parent;//獲取node的父節點，這裡很重要
  5     if (node->lChild==NULL && node->rChild==NULL) //葉子節點直接刪除
  6     {
  7         if (node==node->parent->lChild)
  8         {
  9             node->parent->lChild = NULL;
 10         }
 11         else {
 12             node->parent->rChild = NULL;
 13         }
 14         delete node;
 15         count--;
 16     }
 17     else if (node->rChild != NULL && node->lChild == NULL) {//存在右孩子
 18         if (p==NULL)//說明節點為根節點
 19         {
 20             root = node->rChild;
 21             count--;
 22         }
 23         else {
 24             node->rChild->parent = p;
 25             if (p->lChild==node) //判斷是父節點的左孩子還是右孩子
 26             {
 27                 p->lChild = node->rChild;
 28             }
 29             else {
 30                 p->rChild = node->rChild;
 31             }
 32             delete node;
 33             count--;
 34         }        
 35     }
 36     else if (node->lChild!=NULL && node->rChild==NULL)//存在左孩子
 37     {
 38         if (p==NULL)
 39         {
 40             root = root->lChild;
 41             count--;
 42         }
 43         else {
 44             node->lChild->parent = p;
 45             if (p->lChild==node)
 46             {
 47                 p->lChild = node->lChild;
 48             }
 49             else {
 50                 p->rChild = node->lChild;
 51             }
 52             delete node;
 53             count--;
 54         }
 55     }
 56     else {
 57         BSTNode<T>*left, *curp=NULL;
 58         left = node->rChild; //本方案是找右側最小值，替換node節點，其他節點保持不動即可
 59         while (left!=NULL)
 60         {
 61             curp = left;
 62             left = left->lChild;
 63         }
 64 
 65         if (curp->rChild!=NULL)
 66         {
 67             if (curp->lChild==curp)
 68             {
 69                 curp->parent->lChild = curp->rChild;
 70             }
 71             else {
 72                 curp->parent->rChild = curp->rChild;
 73             }
 74         }
 75         else {
 76             if (curp->parent->lChild==curp)
 77             {
 78                 curp->parent->lChild = NULL;
 79             }
 80             else {
 81                 curp->parent->rChild = NULL;
 82             }
 83             //curp->parent->lChild = NULL;
 84         }
 85         //替curp 替換 node
 86         curp->parent = p;
 87         curp->lChild = node->lChild;
 88         curp->rChild = node->rChild;
 89 
 90         if (p->lChild==node)//判斷node 是p 的左孩子還是右孩
 91         {
 92             p->lChild = curp;
 93         }
 94         else {
 95             p->rChild = curp;
 96         }
 97         delete node;
 98         count--;
 99     }
100 }
View Code

 

第五、二叉樹的搜索查找

由於搜索二叉樹本身是已經排序好的，查找過程相對簡單，從根節點，逐個排查，大於根向右，小於根向左，直到葉子節點. 

template<typename T>
inline BSTNode<T>* BST<T>::search(T k)
{
    BSTNode<T>*node = root;
    while (node!=NULL)
    {
        if (k<node->data)
        {
            node = node->lChild;
        }
        else if (k> node->data)
        {
            node = node->rChild;
        }
        else {
            break;
        }
    }
    return node;
}
View Code

 

第六、二叉搜索樹的排序

根據二叉所有樹的特性，這裡所謂排序，其實就是二叉樹的中序遍歷，其他的幾種遍歷不在這裡贅述，知識調整下結構即可

template<typename T>
void BST<T>::inSort(BSTNode<T>* node)
{
    if (node!=NULL)
    {
        inSort(node->lChild);
        std::cout << node->data<<",";
        inSort(node->rChild);
    }
}
View Code

 

第七、測試程式

 1 #include "pch.h"
 2 #include <iostream>
 3 #include "BSTree.h"
 4 using namespace std;
 5 
 6 int main()
 7 {  
 8     // 樹結構示意
 9     //     30
10     //    /  \
11     //  15   25
12     // /  \
13     //9    18
14     //   /   \
15     //  16   25
16     //      /  \
17     //    20    26  
18     BST<int> sbt;
19     sbt.insert(new BSTNode<int>(30));
20     sbt.insert(new BSTNode<int>(15));
21     sbt.insert(new BSTNode<int>(9));
22     sbt.insert(new BSTNode<int>(18));
23     sbt.insert(new BSTNode<int>(16));
24     sbt.insert(new BSTNode<int>(25));
25     sbt.insert(new BSTNode<int>(20));
26     sbt.insert(new BSTNode<int>(26));
27     sbt.insert(new BSTNode<int>(35));
28 
29     cout << "搜索樹排序後:";
30     sbt.inSort(sbt.root);
31 
32     sbt.deleteNode(18);
33 
34     cout << endl << "刪除18 後排序:";
35 
36     sbt.inSort(sbt.root);
37 }
View Code

測試結果

 所有完整程式代碼

  1 #pragma once
  2 template <typename T> class BST;
  3 template <typename T> class BSTNode {
  4 public:
  5     friend class BST<T>;
  6     BSTNode() {
  7         lChild = rChild = parent = NULL;
  8         data = NULL;
  9     }
 10     BSTNode(T d) {
 11         lChild = rChild = parent = NULL;
 12         data = d;
 13     }
 14 private:
 15     BSTNode<T> *lChild, *rChild, *parent;
 16     T data;
 17 };
 18 
 19 template<typename T> class BST {
 20 public:    
 21     BST() { } 
 22 
 23     //插入操作
 24     void insert(BSTNode<T>*node);
 25 
 26     //二叉查找樹的中序遍歷，就相當於排序了
 27     void inSort(BSTNode<T>*node);
 28 
 29     //按節點刪除
 30     void deleteNode(BSTNode<T>* node);
 31 
 32     //按數值刪除
 33     void deleteNode(const T& t);
 34 
 35     BSTNode<T>* search(T key);
 36     BSTNode<T>* root=NULL;
 37 
 38 private:    
 39     int count;
 40 };
 41 
 42 template<typename T>
 43 void BST<T>::insert(BSTNode<T>* node)
 44 {
 45     BSTNode<T>* curr, *temp = NULL;
 46     curr = root;
 47     while (NULL!= curr) //遍歷二叉樹，找到應該插入的父節點
 48     {
 49         temp = curr;
 50         if (node->data>curr->data)
 51         {
 52             curr = curr->rChild;
 53         }
 54         else {
 55             curr = curr->lChild;
 56         }
 57     }
 58     node->parent = temp;//temp 代碼當前最後遍歷的node，設置node->parent為該節點
 59     if (temp==NULL)
 60     {
 61         root = node;
 62         count++;
 63     }
 64     else {
 65         if (node->data<temp->data)
 66         {
 67             temp->lChild = node;
 68             count++;
 69         }
 70         else {
 71             temp->rChild = node;
 72             count++;
 73         }
 74     }
 75 }
 76 
 77 template<typename T>
 78 void BST<T>::inSort(BSTNode<T>* node)
 79 {
 80     if (node!=NULL)
 81     {
 82         inSort(node->lChild);
 83         std::cout << node->data<<",";
 84         inSort(node->rChild);
 85     }
 86 }
 87 
 88 template<typename T>
 89 inline void BST<T>::deleteNode(BSTNode<T>* node)
 90 {
 91     BSTNode<T>*p = node->parent;//獲取node的父節點，這裡很重要
 92     if (node->lChild==NULL && node->rChild==NULL) //葉子節點直接刪除
 93     {
 94         if (node==node->parent->lChild)
 95         {
 96             node->parent->lChild = NULL;
 97         }
 98         else {
 99             node->parent->rChild = NULL;
100         }
101         delete node;
102         count--;
103     }
104     else if (node->rChild != NULL && node->lChild == NULL) {//存在右孩子
105         if (p==NULL)//說明節點為根節點
106         {
107             root = node->rChild;
108             count--;
109         }
110         else {
111             node->rChild->parent = p;
112             if (p->lChild==node) //判斷是父節點的左孩子還是右孩子
113             {
114                 p->lChild = node->rChild;
115             }
116             else {
117                 p->rChild = node->rChild;
118             }
119             delete node;
120             count--;
121         }        
122     }
123     else if (node->lChild!=NULL && node->rChild==NULL)//存在左孩子
124     {
125         if (p==NULL)
126         {
127             root = root->lChild;
128             count--;
129         }
130         else {
131             node->lChild->parent = p;
132             if (p->lChild==node)
133             {
134                 p->lChild = node->lChild;
135             }
136             else {
137                 p->rChild = node->lChild;
138             }
139             delete node;
140             count--;
141         }
142     }
143     else {
144         BSTNode<T>*left, *curp=NULL;
145         left = node->rChild; //本方案是找右側最小值，替換node節點，其他節點保持不動即可
146         while (left!=NULL)
147         {
148             curp = left;
149             left = left->lChild;
150         }
151 
152         if (curp->rChild!=NULL)
153         {
154             if (curp->lChild==curp)
155             {
156                 curp->parent->lChild = curp->rChild;
157             }
158             else {
159                 curp->parent->rChild = curp->rChild;
160             }
161         }
162         else {
163             if (curp->parent->lChild==curp)
164             {
165                 curp->parent->lChild = NULL;
166             }
167             else {
168                 curp->parent->rChild = NULL;
169             }
170             //curp->parent->lChild = NULL;
171         }
172         //替curp 替換 node
173         curp->parent = p;
174         curp->lChild = node->lChild;
175         curp->rChild = node->rChild;
176 
177         if (p->lChild==node)//判斷node 是p 的左孩子還是右孩
178         {
179             p->lChild = curp;
180         }
181         else {
182             p->rChild = curp;
183         }
184         delete node;
185         count--;
186     }
187 }
188 
189 template<typename T>
190 inline void BST<T>::deleteNode(const T & k)
191 {
192     BSTNode<T>*node = search(k);
193     if (node!=NULL)
194     {
195         deleteNode(node);
196     }
197 }
198 
199 
200 template<typename T>
201 inline BSTNode<T>* BST<T>::search(T k)
202 {
203     BSTNode<T>*node = root;
204     while (node!=NULL)
205     {
206         if (k<node->data)
207         {
208             node = node->lChild;
209         }
210         else if (k> node->data)
211         {
212             node = node->rChild;
213         }
214         else {
215             break;
216         }
217     }
218     return node;
219 }
BSTree.h

 


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • 23種設計模式之享元模式
    享元模式的定義 定義: 使用共用對象可有效的支持大量的細粒度的對象 通俗的說, 就是將類的通用屬性抽出來,建立對象池,以達到限制對象數量的效果 上面定義中要求細粒度對象, 那麼不可避免的使得對象數量多且性質相近, 我們將這些對象的信息分為兩個部分: 內部狀態和外部狀態 說白了,內部狀態就是每個對象都 ...
  • 23種設計模式之橋梁模式
    橋梁模式的定義 定義: 將抽象和實現解耦, 使得兩者可以獨立的變化 通俗的說, 就是一個類調用另一個類中的方法, 需要一個橋梁, 通過聚合的關係調用 其類圖如下: 其中角色說明如下: 抽象角色的部分實現是由實現角色完成的 實現化角色代碼: 具體實現化角色代碼: 抽象化角色代碼: 具體抽象化角色代碼: ...
  • Spring Cloud 微服務項目實現總架構一
    Spring Cloud 服務是一種分散式服務，包括配置管理，服務發現，斷路器，智能路由，微代理，控制匯流排，一次性令牌，全局鎖，主節點選舉， 分散式session, 集群狀態等公共組件。 一 註冊機， Spring Cloud使用erureka server。服務在啟動的時候，會將自己要發佈的服務註 ...
  • 23種設計模式之狀態模式
    狀態模式的定義 定義: 當一個對象內在狀態改變時允許其改變行為, 這個對象看起來像改變了其類 通俗的說, 就是一個事物有不同的狀態,在不同狀態下執行各個方法時有不同的表現, 將每個狀態都封裝成一個類, 然後通過上下文對象統一管理 其類圖如下: 其中的三個角色如下: 抽象狀態角色代碼: 抽象狀態中聲明 ...
  • 對象導論系列---被隱藏的具體實現
    對象導論系列 被隱藏的具體實現 將程式員按角色分為類創建者和客戶端程式員。 客戶端程式員的目標是收集各種用來快速實現應用開發的類。 類創建者的目標是構建類，這種類必須向客戶端暴露必須的服務，而隱藏其她部分。為什麼呢？因為加以隱藏，那麼客戶端程式員將不能訪問她，意味著類創建者可以任意修改被隱藏的部分， ...
  • Yii2設計模式——靜態工廠模式
    利用靜態方法定義一個簡單工廠，這是很常見的技巧，常被稱為靜態工廠(Static Factory)。靜態工廠是 new 關鍵詞實例化的另一種替代，也更像是一種編程習慣而非一種設計模式。和簡單工廠相比，靜態工廠通過一個靜態方法去實例化對象。為何使用靜態方法？因為不需要創建工廠實例就可以直接獲取對象。 ...
  • [SDOI2010] 粟粟的書架
    明顯的二合一問題。貪心的想，要個數最少，那麼久從頁數多的開始選。於是對於前50%的數據，可以直接預處理(1~x,1~y)矩陣內大於等於k的元素個數、元素之和的首碼和，然後二分k值來驗證；對於後50%的數據，已經退化為一維情形，若再使用前面的方法會mle（5e5 1e3 4），那麼考慮使用主席樹來維護 ...
  • GIT學習筆記——第一章
    git之vim編輯器退出命令 張文軍微博主頁 張文軍碼雲主頁 張文軍新浪雲主頁 張文軍博客主頁 剛學習git，好多東西沒接觸過，進入vim後不知道如何出來了，網上找了很多都說是：esc +shift+wq 。 然而我試了好幾次都不行，最後發現是：esc + ： + qw ，這樣就一下退出編輯了。 ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類