【響應式編程的思維藝術】（3）flatMap背後的代數理論Monad

本文是 "Rxjs 響應式編程第二章：序列的深入研究" 這篇文章的學習筆記。示例代碼托管在： "http://www.github.com/dashnowords/blogs" 更多博文： "《大史住在大前端》目錄" [TOC] 一. 劃重點文中使用到的一些基本運算符：映射過濾有限列聚合 ...

一. 劃重點
二. flatMap功能解析
三. flatMap的推演
四. 資料參考

本文是Rxjs 響應式編程-第二章：序列的深入研究這篇文章的學習筆記。

示例代碼托管在：http://www.github.com/dashnowords/blogs

更多博文：《大史住在大前端》目錄

一. 劃重點

文中使用到的一些基本運算符：

map-映射
filter-過濾
reduce-有限列聚合
scan-無限列聚合
flatMap-拉平操作（重點）
catch-捕獲錯誤
retry-序列重試
from-生成可觀測序列
range-生成有限的可觀測序列
interval-每隔指定時間發出一次順序整數
distinct-去除出現過的重覆值

建議自己動手嘗試一下，記住就可以了，有過lodash使用經驗的開發者來說並不難。

二. flatMap功能解析

原文中在http請求拿到獲取到數據後，最初使用了forEach實現了手動流程管理，於是原文提出了優化設想，試圖探究如何依賴響應式編程的特性將手動的數據加工轉換改造為對流的轉換，好讓最終的消費者能夠拿到直接可用的數據，而不是得到一個響應後手動進行很多後處理。在代碼層面需要解決的問題就是，如何在不使用手動遍歷的前提下將一個有限序列中的數據逐個發給訂閱者，而不是一次性將整個數據集發過去。

假設我們現在並不知道有flatMap這樣一個可以使用的方法，那麼先來做一些嘗試：

var quakes = Rx.Observable.create(function(observer) {
    //模擬得到的響應流
    var response = { 
       features:[{
        earth:1
       },{
        earth:2
       }],
       test:1
    }
/*  最初的手動遍歷代碼  
    var quakes = response.features;
        quakes.forEach(function(quake) {
            observer.onNext(quake);
        });*/

    observer.onNext(response);
})
//為了能將features數組中的元素逐個發送給訂閱者，需要構建新的流
.map(dataset){
    return Rx.Observable.from(dataset.features)
}

當我們訂閱quakes這個事件流的時候，每次都會得到另一個Observable，它是因為數據源經過了映射變換，從數據變成了可觀測對象。那麼為了得到最終的序列值，就需要再次訂閱這個Observable，這裡需要註意的是可觀測對象被訂閱前是不啟動的，所以不用擔心它的時序問題。

quakes.subscribe(function(data){
    data.subscribe(function(quake){
        console.log(quake);
    })
})；

如果將Observable看成一個盒子，那麼每一層盒子只是實現了流程式控制制功能性的封裝，為了取得真正需要使用的數據，最終的訂閱者不得不像剝洋蔥似的通過subscribe一層層打開盒子拿到最裡面的數據，這樣的封裝性對於數據在流中的傳遞具有很好的隔離性，但是對最終的數據消費者而言，卻是一件很麻煩的事情。

這時flatMap運算符就派上用場了，它可以將冗餘的包裹除掉，從而在主流被訂閱時直接拿到要使用的數據，從大理石圖來直觀感受一下flatMap:

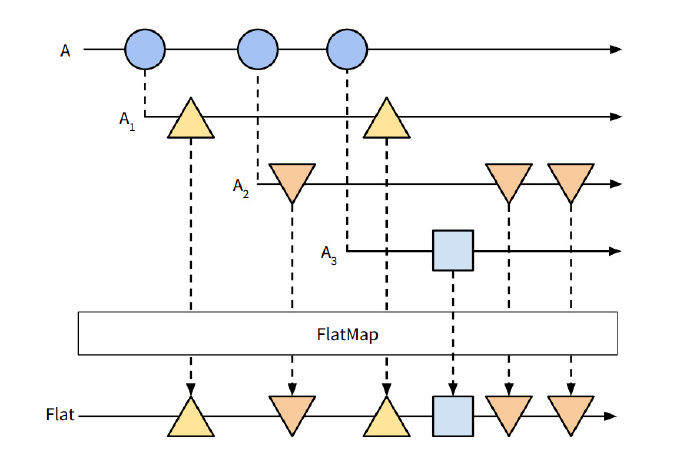
乍看之下會覺得它和merge好像是一樣的，其實還是有一些區別的。merge的作用是將多個不同的流合併成為一個流，而上圖中A1，A2，A3這三個流都是當主流A返回數據時新生成的，可以將他們想象為A的支流，如果你想在支流里撈魚，就需要在每個支流裡布網，而flatMap相當於提供了一張大網，將所有A的支流里的魚都給撈上來。

所以在使用了flatMap後，就可以直接在一級訂閱中拿到需要的數據了：

var quakes = Rx.Observable.create(function(observer) {
    var response = { 
       features:[{
        earth:1
       },{
        earth:2
       }],
       test:1
    }
    observer.onNext(response);
}).flatMap((data)=>{
    return Rx.Observable.from(data.features);
});

quakes.subscribe(function(quake) {
   console.log(quake)
});

三. flatMap的推演

3.1 函數式編程基礎知識回顧

如果本節的基本知識你尚不熟悉，可以通過javascript基礎修煉（8）——指向FP世界的箭頭函數這篇文章來簡單回顧一下函數式編程的基本知識，然後再繼續後續的部分。

/*map運算符的作用
*對所有容器類而言，它相當於打開容器，進行操作，然後把容器再蓋上。
*Container在這裡只是一個抽象定義，為了看清楚它對於容器中包含的值意味著什麼。
*你會發現它其實就是Observable的抽象原型。
*/
Container.prototype.map = function(f){
  return Container.of(f(this.__value))
}

//基本的科里化函數
var curry = function(fn){
  args = [].slice.call(arguments, 1);
  return function(){
     [].push.apply(args, arguments);
     return fn.apply(this, args);
  }
}

//map pointfree風格的map運算符
var map = curry(function(f, any_functor_at_all) {
  return any_functor_at_all.map(f);
});

/*compose函數組合方法
*運行後返回一個新函數，這個函數接受一個參數。
*函數科里化的基本應用，也是函數式編程中運算管道構建的基本方法。
*/
var compose = function (f, g) {
    return function (x) {
        return f(g(x));
    }
};
/*IO容器
*一個簡單的Container實現，用來做流程管理
*這裡需要註意，IO實現的作用是函數的緩存，且總是返回新的IO實例
*可以看做一個簡化的Promise,重點是直觀感受一下它作為函數的
*容器是如何被使用的，對於理解Observable有很大幫助
*/
var IO = function(f) {
  this.__value = f;
}

IO.of = function(x) {
  return new IO(function() {
    return x;
  });
}

IO.prototype.map = function(f) {
  return new IO(compose(f, this.__value));
}

如果上面的基本知識沒有問題，那麼就繼續。

3.2 從一個容器的例子開始

現在來實現這樣一個功能，讀入一個文件的內容，將其中的a字元全部換成b字元，接著存入另一個文件，完成後在控制台輸出一個消息，為了更明顯地看到數據容器的作用，我們使用同步方法並將其包裹在IO容器中，然後利用函數式編程:

var fs = require('fs');

//讀取文件
var readFile = (filename)=>IO.of(fs.readFileSync(filename,'utf-8'));

//轉換字元
var transContent = (content)=>IO.of((content)=>content.replace('a','b'));

//寫入字元串
var writeFile = (content)=>IO.of(fs.writeFileSync('dest.txt',content));

當具體的函數被IO容器包裹起來而實現延遲執行的效果時，就無法按原來的方式使用compose( )運算符直接對功能進行組合，因為readFile函數運行時的輸出結果（一個io容器實例）和transContent函數需要的參數類型（字元串）不再匹配，在不修改原有函數定義的前提下，函數式編程中採用的做法是使用map操作符來預置一個參數：

/*
*map(transContent)是一個高階函數，它的返回函數就可以接收一個容器實例，
*並對容器中的內容執行map操作。
*/
var taskStep12 = compose(map(transContent), readFile);

這裡比較晦澀，涉及到很多功能性函數的嵌套，建議手動推導一下taskStep12這個變數的值，它的結構是這樣一種形式：

io{
    __value:io{
        __value:someComposedFnExpression
    }
}

如果試圖一次性將所有的步驟組合在一起，就需要採用下麵的形式：

var task = compose(map(map(writeFile)),map(transContent),readFile);
//組合後的task形式就是
//io{io{io{__value:someComposedFnExpression}}}

問題已經浮出水面了，每多加一個針對容器操作的步驟，書寫時就需要多包裹一層map，而運行時就需要多進入一層才能觸及組合好的可以實現真正功能的函數表達式，真的是很麻煩。

【響應式編程的思維藝術】 （3）flatMap背後的代數理論Monad