從頭開始學習OI之Tarjan. 今天重新學習了Tarjan演算法..來這裡寫一下學習筆記...但是我太菜了..還是講不好怎麼辦... ...
從頭開始學習OI之Tarjan. 今天重新學習了Tarjan演算法..來這裡寫一下學習筆記...
用處
Tarjan演算法,是一個關於圖的聯通性的神奇演算法.基於DFS(深度優先搜索).是對於有向圖的演算法是.根據樹,棧,打標記等方法來完成剖析一個圖的工作.
我們先來學習一下Tarjan演算法需要知道的定義:
強連通,強連通圖,強連通分量
強連通(Strongly Connected):
在一個有向圖 G 里,有兩個點 a,b ,由a有一條路可以走到b,由b又有一條路可以走到a,我們就叫這兩個頂點 (a,b) 強連通.
強連通圖(Strongly Connected Graph):
如果在一個有向圖 G 中,每兩個點都強連通,我們就叫這個圖 強連通圖。
強連通分量(Strongly Connected Components):
在一個有向圖 G 中,有一個子圖,這個子圖每2個點都滿足強連通,我們就叫這個子圖叫做 強連通分量 (如圖中的 1,2,3 組成的分量就叫強連通分量)
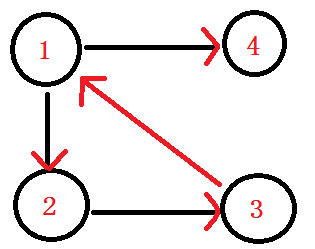
Tarjan演算法:
Tarjan所做的事情很簡單...就是找到每一個強連通分量(單獨一個點也算是強連通分量..) 在實現演算法之前...我們先定義幾個數組:
dfn[i] 表示第 i 個節點的時間戳..也就是在DFS這張圖的時候這個點被遍歷到的時刻..
low[i] 表示第 i 個節點所在的強連通分量的根節點(按理說強連通分量無所謂根節點..這裡的根節點是指在那一棵DFS樹中這個強連通分量的根節點)
很明顯如果 dfn[i] == low[i] 那麼就代表這一個點是一個強連通分量的根
先看一下演算法流程
void Tarjan(int u) {
dfn[u] = low[u] = ++Index; //將dfn和low都初始化為時間戳,也就是dfs到的時刻
Stack[++top] = u; //將該點壓入dfs棧中
vis[u] = 1; //標記點在棧中
for(int i = head[u]; i; i = edge[i].next) { //DFS過程
if(!dfn[edge[i].to]) { //如果該點沒有被搜索到過
Tarjan(edge[i].to); //對於該點進行演算法(即dfs的過程)
low[u] = min(low[u],low[edge[i].to]); //搜索完成返回時更新一下這個強連通分量里的所有點的在dfs樹中的根節點
} else if(vis[edge[i].to]) { //如果該點已經在搜索棧中,那麼代表當前棧中在這個點後的點在一個強連通分量里,那麼這個搜索到的點就是這個強連通分量的根節點..
low[u] = min(low[u],dfn[edge[i].to]); //將當前點所在強連通分量的根節點修改為搜索到的這個節點,也就是根節點..
}
}
if(dfn[u] == low[u]) { //按照上面的定義我們知道這是判斷是否是一個強連通分量的根節點
while(Stack[top] != u) { //按照上面所說的將該點在棧後的所有節點都彈出(在一個強連通分量里..也就是我們要求的了..可以染色存儲起來備用或者縮成一個點(縮點演算法))
printf("%d ",Stack[top]);
vis[Stack[top--]] = 0;
}
printf("%d\n",Stack[top]); //彈出當前的這個根
vis[Stack[top--]] = 0;
}
}首先來一張有向圖 \(G\).我們一點一點來模擬整個演算法.
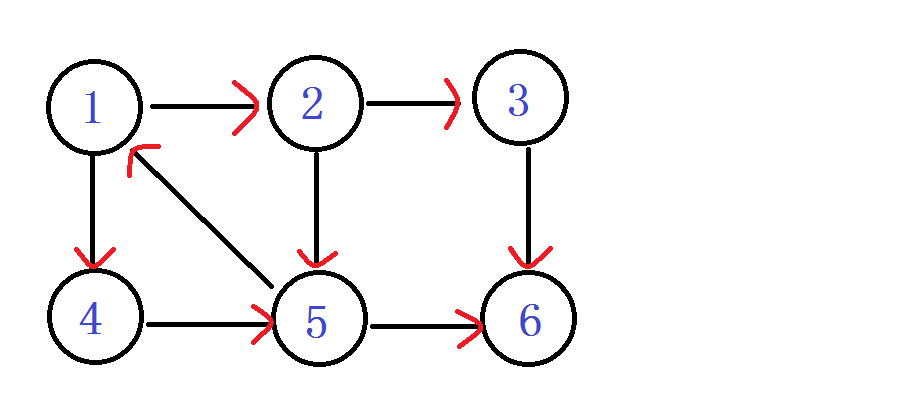
首先是一點一點的入棧..也就是上面DFS遍歷的時候的順序..叫做DFS序或者入棧序..即:
Step1: 1號點入棧 dfn[1] = low[1] = ++index (1)
此時棧為: 1
Step2: 2號點入棧 dfn[2] = low[2] = ++index (2)
此時棧為: 1 2
Step3: 3號點入棧 dfn[3] = low[3] = ++index (3)
此時棧為: 1 2 3
Step4: 6號點入棧 dfn[6] = low[6] = ++index (4)
此時棧為: 1 2 3 6
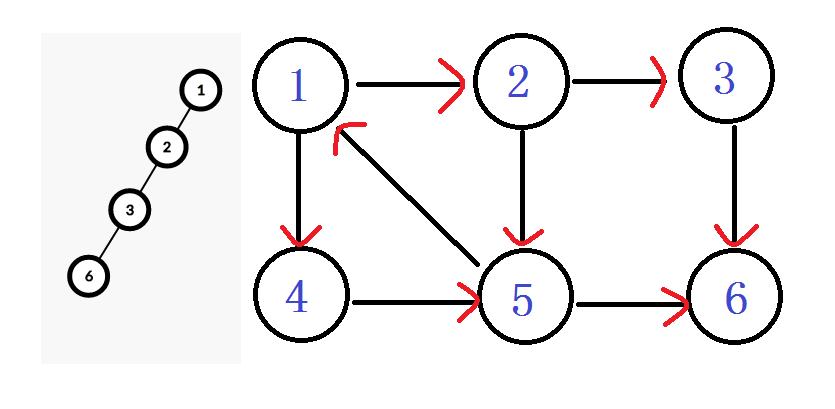
左邊這張樹的圖就是當前操作完成後的DFS樹...
走到這裡之後我們看到右邊圖中六號節點沒有了出邊...也就是上面說的第一步或者說是第一個判斷結束了...
我們就要開始返回了,明顯 low[6] == dfn[6] 所以6就是一個強連通分量的根節點;
棧要一直彈出直到彈出6號節點 此時棧為: 1 2 3
然後返回到三號..三號再無出邊..
也一直彈出直到將其彈出 存為一個強連通分量的根 此時棧為: 1 2
發現2號節點還有可以繼續遍歷下去的邊..於是將五號節點壓入棧中即:
dfn[5] = dfn[5] = ++index(5) 此時棧為: 1 2 5
再遍歷發現一個6號..已經遍歷過就不在管他了..
再遍歷發現一個1號節點..1號在棧中..於是進入第二個if語句,修改
low[5] = min(low5,low1) 所以 low[5] 也就是五號節點所在的強連通分量的根就是1
五號沒有出邊了..返回上一層..修改 low[2] = min(low2,low5),low[2] = 1
二號沒有出邊了..返回上一層..修改 low[1] = min(low1,low2),low[1] = 1 low[1]依然等於1
一號還有出邊..遍歷到四號 dfn[4] = low[4] = ++index(6) 此時棧為 1 2 5 4
四號遍歷到五號..五號在棧中所以更新一下 low[4] = min(low4,low5),low[4] = 1;
再返回 low[1] = min(low1,low4) ,low[1] = 1;
然後1號也沒有出邊了..這時棧一直彈出直到將1號彈出 棧空
最後的DFS樹是這樣的
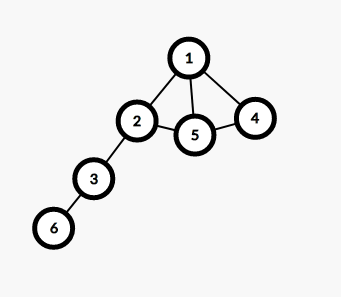
按照我們找到的根節點拆成一個個的強連通分量
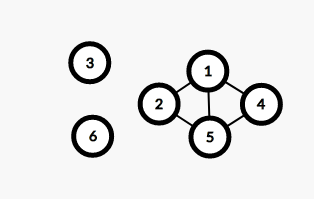
這樣就完成了
我們把以一號為開始的連通圖都遍歷一遍了...為了防止圖有多個(不連通) 我們要在調用Tarjan的時候這樣寫
for(int i = 1; i <= n; ++i)
if(!dfn[i]) Tarjan(i); //如果沒有時間戳,那就代表沒有遍歷到,從此點開始Tarjan這樣就可以把所有的圖都給遍歷一遍了...
來一道裸代碼。
輸入:
一個圖有向圖。
輸出:
它每個強連通分量。
這個圖就是剛纔講的那個圖。一模一樣。
Input:
6 8
1 3
1 2
2 4
3 4
3 5
4 6
4 1
5 6
Output:
6
5
3 4 2 1
代碼:
#include <cstdio>
#include <algorithm>
using namespace std;
struct node {
int to,next;
} edge[1001];
int cnt,Index,top;
int dfn[1001],low[1001];
int stack[1001],head[1001],visit[1001];
void add(int x,int y) {
edge[++cnt].next = head[x];
edge[cnt].to = y;
head[x] = cnt;
}
void tarjan(int x) { //代表第幾個點在處理。遞歸的是點。
dfn[x] = low[x] = ++Index; // 新進點的初始化。
stack[++top] = x; //進棧
visit[x] = 1; //表示在棧里
for(int i = head[x]; i; i = edge[i].next) {
if(!dfn[edge[i].to]) { //如果沒訪問過
tarjan(edge[i].to); //往下進行延伸,開始遞歸
low[x] = min(low[x],low[edge[i].to]);//遞歸出來,比較誰是誰的兒子/父親,就是樹的對應關係,涉及到強連通分量子樹最小根的事情。
} else if(visit[edge[i].to]) { //如果訪問過,並且還在棧里。
low[x] = min(low[x],dfn[edge[i].to]);//比較誰是誰的兒子/父親。就是鏈接對應關係
}
}
if(low[x] == dfn[x]) { //發現是整個強連通分量子樹里的最小根。
do {
printf("%d ",stack[top]);
visit[stack[top]] = 0;
top--;
} while(x != stack[top+1]);//出棧,並且輸出。
printf("\n");
}
return ;
}
int main() {
int n,m;
scanf("%d%d",&n,&m);
int x,y;
for(int i = 1; i <= m; i++) {
scanf("%d%d",&x,&y);
add(x,y);
}
for(int i = 1; i <= n; i++)
if(!dfn[i]) tarjan(i);//當這個點沒有訪問過,就從此點開始。防止圖沒走完
return 0;
}


