前面介紹的數組容納的是一串數字,仿佛一根線把這組數字串了起來,故而它只是一維數組。一維數組用來表示簡單的數列尚可,要是表達複雜的平面坐標系,那就力不從心了。由於平面坐標系存在水平和垂直兩個方向,因此可用二維數組來保存平面坐標繫上的一組坐標頂點,其中第一維是頂點隊列,第二維是頂點的橫縱坐標。許多個平面 ...
前面介紹的數組容納的是一串數字,仿佛一根線把這組數字串了起來,故而它只是一維數組。一維數組用來表示簡單的數列尚可,要是表達複雜的平面坐標系,那就力不從心了。由於平面坐標系存在水平和垂直兩個方向,因此可用二維數組來保存平面坐標繫上的一組坐標頂點,其中第一維是頂點隊列,第二維是頂點的橫縱坐標。許多個平面組合起來變成一幅動畫,每個平面都構成動畫的一個幀,這樣就形成了三維數組。二維數組、三維數組,乃至更多維度的數組,統稱為多維數組。多維數組全由一維數組擴展而來,它們的用法大同小異,因而只要學會如何使用二維數組,即可舉一反三運用其他多維數組。下麵就以二維數組為例,統一介紹多維數組的常見用法。
如同一維數組那樣,二維數組也有兩種聲明形式,一種是在變數名稱後面添加兩對方括弧,例如“double triangle[][]”;另一種是在類型後面添加兩對方括弧,例如“int[][] triangle”。前述的二維數組triangle表示平面坐標繫上的三角形,其中第一對方括弧表示這個三角形有幾個頂點,第二對方括弧表示每個頂點由幾個坐標方向構成。
給二維數組分配存儲空間也有三種方式,分別說明如下:
1、利用語句“new 變數類型[頂點數量][方向數量]”分配空間,比如三角形triangle有三個頂點,每個頂點由橫縱兩個坐標方向組成,則可通過下麵這行語句實現:
// 在兩對方括弧內分別填入數字,表示數組有多少行多少列 triangle = new double[3][2];
2、在分配存儲空間的時候立即對數組進行初始化賦值,此時方括弧中間不填數字,而在方括弧後面添加花括弧,並且花括弧內部是以逗號分隔的幾個一維數組。此時初始化賦值的代碼如下所示:
// 方括弧內留空,然後緊跟花括弧,花括弧內部是以逗號分隔的幾個一維數組
double[][] triangle = new double[][]{
new double[]{-2.0, 0.0},
new double[]{0.0, -1.0},
new double[]{2.0, 1.0}
};
3、可見上面的第二種寫法實在啰嗦,完全可以參照一維數組的簡化寫法,把多餘的“new double***”統統去掉,於是整個初始化代碼精簡如下:
// 賦值等號右邊直接跟著花括弧,花括弧又內嵌好幾個花括弧分別表示對應的一維數組
double[][] triangle = { {-2.0, 0.0}, {0.0, -1.0}, {2.0, 1.0} };
以上的賦值等號右邊直接跟著花括弧,花括弧裡面又有三組花括弧,每組花括弧分別容納兩個數字。這便告訴編譯器:該二維數組需要分配三個頂點,並且每個頂點都有兩個坐標方向。
若要獲取二維數組裡面的某個元素,可採取“數組名稱[元素行號][元素列號]”的形式,表示當前操作的是第幾行第幾列的數組元素。與一維數組不同的是,對於二維數組來說,“數組名稱.length”不能獲得所有元素的數量,而是獲得該數組的行數;要想獲取某行的列數,則需通過“triangle[行號].length”來得到,把所有行的列數累加起來,才能求得該二維數組的元素個數。下麵是聲明一個浮點型的二維數組,並對每個數組元素賦值,最後遍歷列印各元素的完整代碼例子:
// 以下是聲明二維數組的第一種形式:“變數類型 數組名稱[][]”
double triangle[][];
// 以下是分配二維數組空間的第一種形式
// 在兩對方括弧內分別填入數字,表示數組有多少行多少列
triangle = new double[3][2];
// 數組名稱後面的“[數字1][數字2]”,就是數組元素的行列下標,表示當前操作的是第幾行第幾列的數組元素
triangle[0][0] = -2.0;
triangle[0][1] = 0.0;
triangle[1][0] = 0.0;
triangle[1][1] = -1.0;
triangle[2][0] = 2.0;
triangle[2][1] = 1.0;
// 下麵通過迴圈語句依次讀出數組中的所有元素。
// “二維數組名稱.length”表示獲取該數組的行數
for (int i=0; i<triangle.length; i++) {
// “triangle[i].length”表示獲取該數組第i行的列數
for (int j=0; j<triangle[i].length; j++) {
// 列印第i行第j列的數組元素
System.out.println("triangle["+i+"]["+j+"]="+triangle[i][j]);
}
}
上述示例代碼中的二維數組,存放了平面坐標繫上的三個頂點,它們的坐標分別是(-2.0, 0.0)、(0.0, -1.0)、(2.0, 1.0)。這三個坐標點構成了一個三角形的三個頂點,正如下圖所示的A點(坐標為(-2,0))、B點(坐標為(0,-1))、C點(坐標為(2,1))。
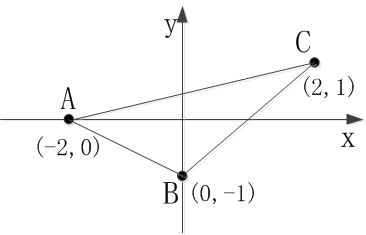
看到了熟悉的平面坐標圖,這下平面幾何的知識可派上用場了,例如根據兩點的坐標來計算兩點之間的距離。既然三角形有三個頂點A、B、C,接下來不妨計算它的三條邊長,包括AB、AC和BC三條邊的長度。於是分別求得兩個頂點在橫軸方向的距離,以及在縱軸方向的距離,然後利用勾股定理算出連接兩頂點的斜邊長度。以下便是由二維數組保存的坐標數值求解三角形各邊長的演示代碼:
// 下麵通過迴圈語句依次計算三角形每條邊的長度
// 假設第一個數組元素代表點A,第二個數組元素代表點B,第三個數組元素代表點C,
// 則本迴圈將依次求得AB、AC、BC這三條邊的長度
for (int i=0; i<triangle.length-1; i++) {
for (int j=i+1; j<triangle.length; j++) {
// 獲取兩個頂點在橫軸方向的距離
double xDistance = Math.abs(triangle[j][0] - triangle[i][0]);
// 獲取兩個頂點在縱軸方向的距離
double yDistance = Math.abs(triangle[j][1] - triangle[i][1]);
// 根據勾股定理計算連接兩頂點的斜邊長度
double distance = Math.sqrt(xDistance*xDistance + yDistance*yDistance);
System.out.println("i="+i+",j="+j+",distance="+distance);
}
}
運行上述的演示代碼,列印出來的三角形邊長計算結果如下所示:
i=0,j=1,distance=2.23606797749979 i=0,j=2,distance=4.123105625617661 i=1,j=2,distance=2.8284271247461903


