一、什麼是集合 集合就是不同對象的無序聚集。那麼鏈表和集合有什麼關係呢?我們來變個魔術。如下圖是各種顏色組成的鏈表: 下麵我們一步步把鏈表變成集合。 第一步砍去鏈接 第二步去掉重覆 第三步放到一個框里搖一搖就成集合了 可以看出集合有這些特點: 無序:鏈表去掉鏈接,就是去掉元素間有序狀態。 不重覆:去 ...
一、什麼是集合
集合就是不同對象的無序聚集。那麼鏈表和集合有什麼關係呢?我們來變個魔術。如下圖是各種顏色組成的鏈表:

下麵我們一步步把鏈表變成集合。
第一步砍去鏈接

第二步去掉重覆

第三步放到一個框里搖一搖就成集合了
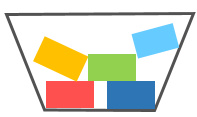
可以看出集合有這些特點:
- 無序:鏈表去掉鏈接,就是去掉元素間有序狀態。
- 不重覆:去掉重覆的玫紅色。
雖然說集合是一種數學概念,但在實際生活中無處不透露著集合。比如一個班級的學生是一個集合。班級里的男生又是一個集合。
二、集合的結構

大衛哥這裡為了簡化概念的描述,繼續用單鏈表來表示集合,但是在對集合做計算的時候單鏈表並不合適,數據量大的時候它的弊端就會顯現,在講到後面的數據結構和演算法的時候,我們再回頭來完善前面講的數據介面的實現。
三、介面說明及實現
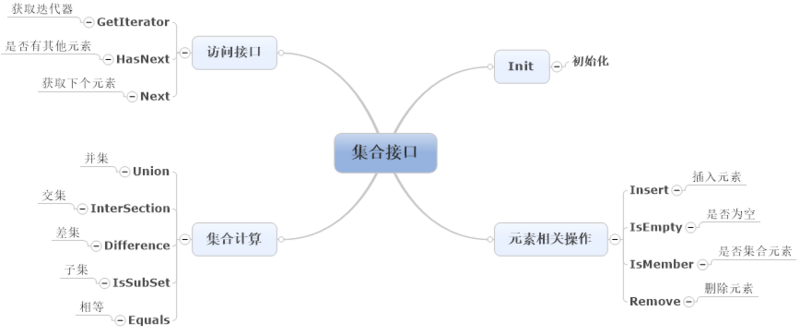
1、Init
初始化集合,本質是初始化鏈表。
func (set *Set) Init(match ...MatchFun) {
lst := new(List)
(*set).list = lst
if len(match) == 0 {
lst.Init()
} else {
lst.Init(match[0])
}
}要比較集合中的元素,我們得傳入一個比較函數,這裡的match是我們的自定義類型MatchFun,大家可以查看代碼里的定義。
2、Insert
把元素放入集合中。
func (set *Set) Insert(data Object) bool {
if (!set.IsMember(data)) {
return (*set).list.Append(data)
}
return false
}3、IsEmpty
是否是空集合。
func (set *Set) IsMember(data Object) bool {
return (*set).list.IsMember(data);
}4、IsMember
是否是集合元素。
func (set *Set) IsMember(data Object) bool {
return (*set).list.IsMember(data);
}5、Remove
刪除指定集合元素。
func (set *Set) Remove(data Object) bool {
return (*set).list.Remove(data)
}6、Union
並集計算。
func (set *Set) Union(set1 *Set) *Set {
if (set1 == nil) {
return nil
}
nSet := new(Set)
nSet.Init((*((*set).list)).myMatch)
if (set.IsEmpty() && set1.IsEmpty()) {
return nSet
}
for i := uint64(0); i < set.getSize(); i++ {
nSet.Insert(set.getAt(i))
}
var data Object
for i := uint64(0); i < set1.getSize(); i++ {
data = set1.getAt(i)
if (!nSet.IsMember(data)) {
nSet.Insert(data)
}
}
return nSet
}計算set和set1的並集。
7、InterSection
計算交集。
func (set *Set) InterSection(set1 *Set) *Set {
if (set1 == nil) {
return nil
}
nSet := new(Set)
nSet.Init((*((*set).list)).myMatch)
if (set.IsEmpty() || set1.IsEmpty()) {
return nSet
}
fSet := set
sSet := set1
lenth := set.getSize()
if (set1.getSize() < lenth) {
fSet = set1
sSet = set
}
var data Object
for i := uint64(0) ; i < lenth; i++ {
data = fSet.getAt(i)
if (sSet.IsMember(data)) {
nSet.Insert(data)
}
}
return nSet
}8、Difference
計算差集。
func (set *Set) Difference(set1 *Set) *Set {
if (set1 == nil) {
return nil
}
nSet := new(Set)
nSet.Init((*((*set).list)).myMatch)
if (set.IsEmpty()) {
return nSet
}
var data Object
for i := uint64(0); i < set.getSize(); i++ {
data = set.getAt(i)
if (!set1.IsMember(data)) {
nSet.Insert(data)
}
}
return nSet
}返回的集合是屬於set,但不屬於set1的集合。
9、IsSubSet
func (set *Set) IsSubSet(subSet *Set) bool {
if (set == nil) {
return false
}
if (subSet == nil) {
return true
}
for i := uint64(0); i < subSet.getSize(); i++ {
if (!(set.IsMember(subSet.getAt(i)))) {
return false
}
}
return true
}確認subSet是否是set的子集。
10、Equals
func (set *Set) Equals(set1 *Set) bool {
if (set == nil || set1 == nil) {
return false
}
if (set.IsEmpty() && set1.IsEmpty()) {
return true
}
nSet := set.InterSection(set1)
return (set.getSize() == nSet.getSize())
}判斷set和set1中集合元素是否一樣。
11、訪問集合元素
因為集合是沒有順序的,所以沒法用序號來訪問集合元素(雖然這裡是用單鏈表實現)。這裡我們用迭代器的方式來實現元素的訪問。首先我們定義一個迭代器的介面。
(1) Iterator
type Iterator interface{
HasNext() bool
Next() Object
}(2) SetIterator
type SetIterator struct {
index uint64
set *Set
}因為Iterator是介面,沒法保存狀態,所以我們得定義一個類型來保存每次訪問的游標。這裡的游標是序號。
(3) GetIterator
返回一個實現了Iterator介面的對象。
func (set *Set) GetIterator() *SetIterator {
iterator := new(SetIterator)
(*iterator).index = 0
(*iterator).set = set
return iterator
}(4) HasNext
是否有其他元素沒訪問到?
func (iterator *SetIterator) HasNext() bool {
set := (*iterator).set
index := (*iterator).index
return (index < set.getSize())
}這是Iterator中HasNext方法的實現。
(5) Next
獲取其他元素。
func (iterator *SetIterator) Next() Object {
set := (*iterator).set
index := (*iterator).index
if (index < set.getSize()) {
data := set.getAt(index)
(*iterator).index++
return data
}
return nil
}四、小結
集合在概率中有很多應用,這裡我們僅僅是用單鏈表簡單的實現了集合,在大量數據下,計算效率很低。隨著學習的深入,我們會優化這些數據介面的實現。
代碼下載


