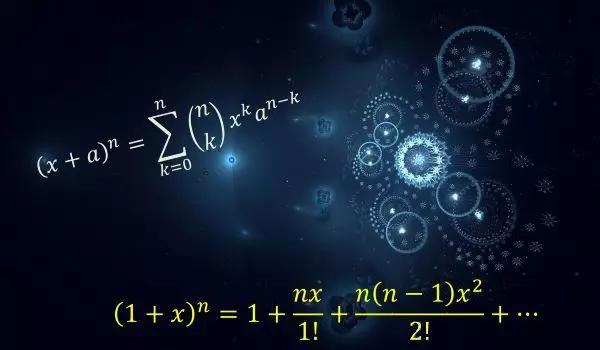很多同學想從事數據科學崗位,對於這個崗位而言,數學知識的儲備重要嗎? 答案顯而易見,掌握好數學對於從事該崗位而言是很重要的。數學一直是任何當代科學學科的基礎,幾乎所有的現代數據科學技術(包括所有的機器學習)都有一些深刻的數學知識。在本文中,我們將討論想成為一名優秀的數據科學家應該掌握的基本數學知識, ...
很多同學想從事數據科學崗位,對於這個崗位而言,數學知識的儲備重要嗎?
答案顯而易見,掌握好數學對於從事該崗位而言是很重要的。數學一直是任何當代科學學科的基礎,幾乎所有的現代數據科學技術(包括所有的機器學習)都有一些深刻的數學知識。在本文中,我們將討論想成為一名優秀的數據科學家應該掌握的基本數學知識,以便在各個方面都能很好地適應。
介紹
有時候,作為一名數據科學家(甚至是團隊的初級分析師),你必須全心全意地學習那些基礎的數學知識,或者正確地應用這些技術,有時候你可以通過使用一些API或者拿來即用的演算法完成相關任務。
但是,如果你對用於為用戶創建有意義的產品推薦演算法背後的數學知識有充分的瞭解,這將永遠不會對你有任何損害。通常情況下,懂得這些知識應該能讓你在同齡人中占有一席之地。
毫無疑問,想成為一名頂級的數據科學家還需要掌握其他領域的知識,比如編程能力、具有一定的商業頭腦,以及對數據的獨特分析和好奇心態。本文所要做的就是整理一份最基本的數學技能指南,以幫助你更好地完成這項工作。
對“新手”特別重要
對於那些在其他領域花費大量時間並想進入這一領域的專業人士來說,基礎學知識顯得尤其重要,比如硬體工程、零售、化學加工工業、企業管理等領域。
雖然這些領域的工作中也涉及電子錶格、數值計算和預測方面的內容,但在數據科學實踐中對必要的數學技能要求卻大不相同。
為什麼以及如何與眾不同——這是科學而不是數據
考慮一個Web開發人員(或業務分析師),他可能每天需要處理大量的數據和信息,但可能沒有強調對該數據進行建模。通常,數據分析的任務重點在於“ 根據需求利用數據並繼續推進項目 ”,而不是深入探索,數據科學應該始終關註科學(而不是數據)。某些工具和技術會變得不可或缺,其中大多數是科學處理過程的特點:
- 通過探測潛在的動態來建模過程
- 構建假設
- 嚴格評估數據源的質量
- 量化數據和預測的不確定性
- 培養個人從信息流中識別隱藏模式的感覺
- 清楚地瞭解模型的局限性
- 理解數學證明及其背後的所有抽象邏輯
這類的培訓,大多數沒有考慮正數而是講解抽象的數學實體(及其屬性和相互關係),被認為是四年制大學學位課程標準課程的一部分。個人不需要以優異的成績從頂尖大學畢業來獲得這種水平的數學知識,但不幸的是,過去的訪問量幾乎在變少。
展示成功的藍圖
一般而言,沒有通用的藍圖。就其本質而言,數據科學並不依賴於特定的學科領域,並且可能是在單個項目中處理各種現象,如癌症診斷和社會行為分析等,這會產生各種令人眼花繚亂的n維數學對象、統計分佈、優化目標函數等。
上面提到的那些東西是什麼?如果你對其補熟悉的話,以下是我們需要學習、吸收的內容建議。
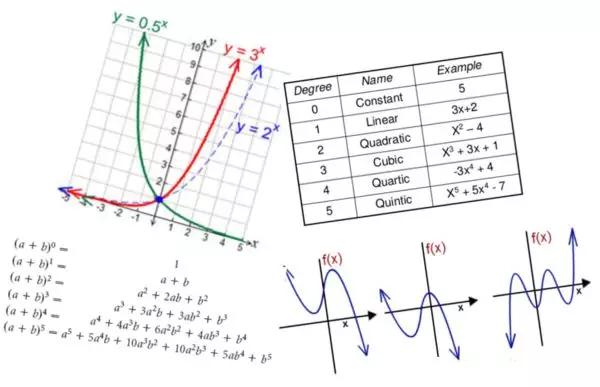
函數、變數、方程、圖
What:從基本的知識開始,如線的方程式到二項式定理及其性質。
- 對數、指數、多項式函數、有理數
- 基本幾何和定理,三角恆等式
- 實數和複數的基本屬性
- 級數、總和和不等式
- 圖表和繪圖、笛卡爾和極坐標系統、圓錐曲線
示例:如果想瞭解在排序後在百萬項目資料庫上搜索的運行速度,你將會遇到二進位搜索的概念。為了理解它的行為,需要理解對數和遞推方程。或者是分析時間序列的話,可能會遇到周期函數和指數衰減等概念。
學習資源:
數據科學數學技能——Coursera
https://www.coursera.org/learn/datasciencemathskills
代數簡介——edX
https://www.edx.org/course/introduction-algebra-schoolyourself-algebrax-1
代數——可汗學院
https://www.khanacademy.org/math/algebra
統計
What:成長為數據科學家必須知道的知識。在關於數據科學的討論中,再如何強調掌握統計和概率的基本概念的重要性都不為過。該領域的許多從業者實際上稱經典機器學習(非神經網路)只是統計學習。該主題內容非常廣泛,重點規劃大多數的基本概念即可。
- 數據摘要和描述性統計、集中趨勢、方差、協方差及相關性
- 基本概率:基本概念、期望、概率演算、貝葉斯定理、條件概率
- 概率分佈函數:均勻、標準、二項式、卡方、學生t分佈、中心極限定理、
- 採樣、測量、錯誤、隨機數生成
- 假設檢驗、A / B檢驗、置信區間、p值,
- 方差分析、t檢驗
- 線性回歸,正則化
示例:在面試時,作為一名潛在的數據科學家,如果你能掌握上面提到的所有概念,你會很快地給對方留下深刻的印象。作為數據科學家,你幾乎每天都會使用上述中的一些概念。
學習資源:
R專業統計學——Coursera
https://www.coursera.org/specializations/statistics
使用Python進行數據科學的統計和概率—— edX
https://courses.edx.org/courses/course-v1:UCSanDiegoX+DSE210x+3T2017/course/
商業統計與分析專業—— Coursera
https://www.coursera.org/specializations/business-statistics-analysis
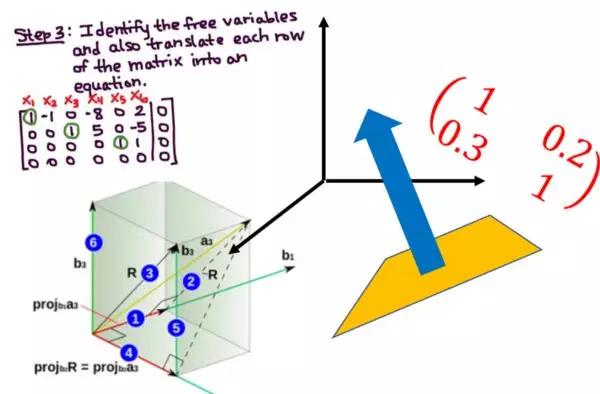
線性代數
What:社交網路軟體上的朋友推薦、音樂APP中的歌曲推薦以及使用深度遷移學習將自拍照轉換為其它風格的圖像,這些都有用到線性代數的知識。線性代數是數學領域的一個重要分支,用於理解大多數機器學習演算法如何在數據流上工作以創建洞察力。以下是要學習的基本內容:
- 矩陣和向量的基本屬性——標量乘法、線性變換、轉置、共軛、秩、行列式
- 內積外積、矩陣乘法法則和各種演算法、逆矩陣
- 特殊矩陣——方陣、單位矩陣、三角矩陣、稀疏和密集矩陣、單位向量、對稱矩陣、埃爾米特矩陣、斜埃爾米特矩陣和酉矩陣,
- 矩陣分解、高斯/高斯-若爾消除法,求解Ax = b方程的線性系統
- 矢量空間、基、跨度、正交性、線性最小二乘,
- 特征值、特征向量和對角化,奇異值分解(SVD)
示例:如果你使用過主成分分析(PCA)降維技術,那麼你可能已經使用過奇異值分解來實現數據集的緊湊維度表示,使得參數更少。所有神經網路演算法都使用線性代數技術來表示和處理網路結構和學習操作。
學習資源:
線性代數基礎—— edX
https://courses.edx.org/courses/course-v1:UTAustinX+UT.5.05x+2T2017/course/
機器學習數學:線性代數——Coursera
https://www.coursera.org/learn/linear-algebra-machine-learning
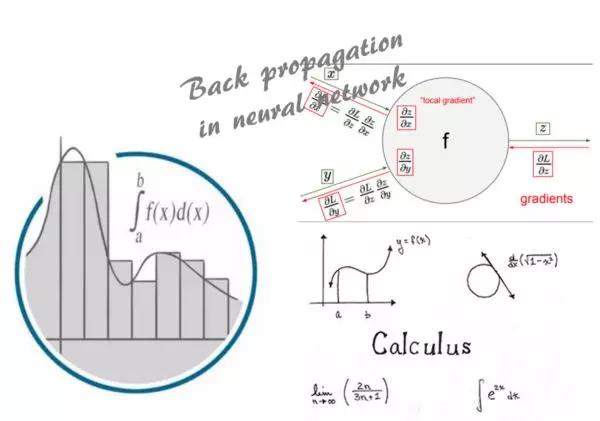
微積分
What:無論你在大學期間喜歡它還是討厭它,在數據科學或機器學習領域的許多地方都會應用微積分的概念。它隱藏線上性回歸中最小二乘問題的簡單分析解決方案背後,或者嵌入到神經網路學習新模式的每個反向傳播中。以下是要學習的內容:
- 單變數、極限、連續性和可微性的函數
- 中值定理、不確定性和洛必達法則
- 極大值和極小值
- 乘積和鏈式法則
- 泰勒級數、無窮級數求和/積
- 積分計算和中值定理、對有限和不正確積分的評價,
- Beta和Gamma函數
- 多變數函數、極限、連續性、偏導數
- 普通和偏微分方程的基礎知識
示例:如何實現邏輯回歸演算法,它很有可能使用一種稱為“梯度下降”的方法來找到最小損失函數。要瞭解其如何工作,需要使用來自微積分的基本概念——梯度、導數、極限和鏈式法則。
學習資源:
大學前掌握的微積分——edX
https://www.edx.org/course/pre-university-calculus
可汗學院的微積分全部內容
https://www.khanacademy.org/math/calculus-home
機器學習數學:多變數微積分——Coursera
https://www.coursera.org/learn/multivariate-calculus-machine-learning
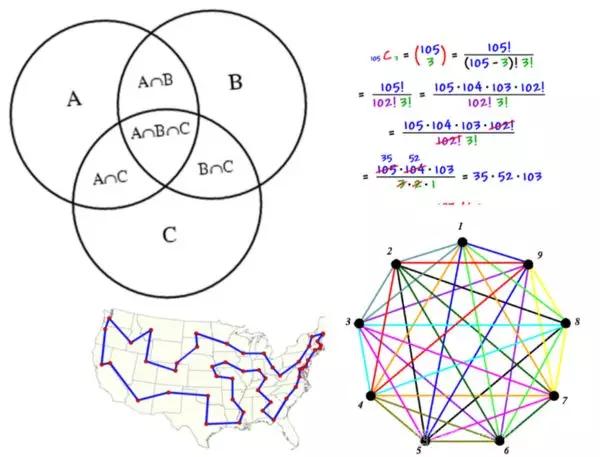
離散數學
What:這部分內容通常是“數據科學數學”方案中較少討論的主題,但事實是所有現代數據科學都是在計算系統的幫助下完成的,離散數學是這類系統的核心。要學習的內容:
- 集合、子集和冪集
- 計數函數、組合學、可數性
- 基本證明技術——歸納法、反證法
- 歸納、演繹和命題邏輯的基礎知識
- 基本數據結構——堆棧、隊列、圖、數組、哈希表、樹
- 圖表屬性——連接組件、度、最大流量/最小切割概念、圖形著色
- 遞歸關係和方程
- 函數的增長和O(n)符號概念
示例:在任何社交網路分析中,你需要知道圖的屬性和快速演算法以搜索和遍歷整個網路。在選擇任何演算法時,都需要通過使用 O(n)表示法來瞭解時間和空間複雜度。
學習資源:
電腦科學專業的離散數學概論—— Coursera
https://www.coursera.org/specializations/discrete-mathematics
數學思維導論——Coursera
https://www.coursera.org/learn/mathematical-thinking
掌握離散數學:集合、數學邏輯—— Udemy
https://www.udemy.com/master-discrete-mathematics/
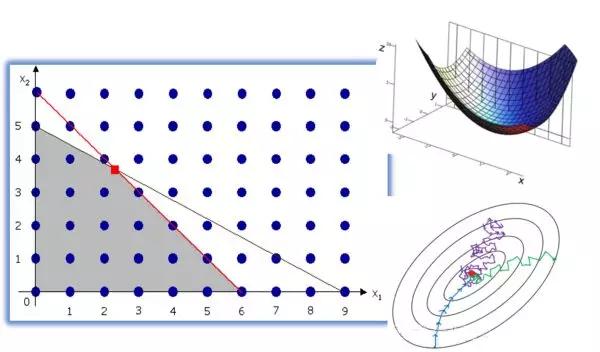
最優化、運籌學
What:這些主題與應用數學中的傳統話語沒什麼不同,因為它們在專業領域——理論電腦科學、控制理論或運籌學中最為相關和最廣泛使用。實際上,每種機器學習演算法旨在最小化受各種約束影響的某種估計誤差,這就是優化問題。要學習的內容:
- 優化的基礎——如何制定問題
- 最大值、最小值、凸函數、全局解
- 線性規劃、單純形演算法
- 整數規劃
- 約束編程、背包問題
示例:使用最小平方損失函數的簡單線性回歸問題通常具有精確的解析解,但邏輯回歸問題卻沒有,要理解其中的原因,需要瞭解優化中凸性的概念,這也將闡明為什麼我們必須對大多數機器學習問題中的“近似”解決方案能夠滿意。
資源:
業務分析中的優化方法 ——edX
https://courses.edx.org/courses/course-v1:MITx+15.053x+3T2016/course/
離散優化—— Coursera
https://www.coursera.org/learn/discrete-optimization
確定性優化 ——edX
https://www.edx.org/course/deterministic-optimization-0
結束語
作為一名數據科學家,需要掌握這麼多的知識,看起來似乎有些讓人絕望,但你不需要感到害怕,網路上資源很多,可以根據個人需求定製自己的學習資源列表。在複習這些知識並學習新概念之後,個人能力會有很大的提升,這是成為數據科學家的一大飛躍。