Size Balanced Tree 挺有意思的, 適合新手練習 ...
引言 - 初識 Size Balanced Tree
最近在抽細碎的時間看和學習 random 的 randnet 小型網路庫.
iamrandom/randnet - https://github.com/iamrandom/randnet (1)
瞭解到 陳啟峰 2006-12-29 高中的時候寫的論文 Size Balanced Tree(一種變種的 AVI 樹) 感覺好精彩.
就著手翻譯成實戰代碼.
陳啟峰 Size Balanced Tree - https://files.cnblogs.com/files/life2refuel/%E9%99%88%E5%90%AF%E5%B3%B0%E3%80%8ASize-Balanced-Tree%E3%80%8B.pdf (2)
翻譯過程中前驅和後繼參照了下麵同行的代碼
二叉查找樹的前驅後繼 - http://www.cnblogs.com/Renyi-Fan/p/8252227.html (3)
: ) - , -
推薦朋友學習的時候, 可以先看 (2) 和 (3) . 其中 (3) 最簡單, 看完之後應該收穫滿滿.
對於 (2) 還是深深佩服的, 畢竟一樣大時候, 才剛脫離趣味玩泥巴. 大佬就可以證明演算法的完備性. 如果你看到
(2) 證明部分, 這裡不妨補充一些關於 f[h] 求證過程.

其實也就是高中二階等比數列求證.
那後面就開始扯了正題了 : ) 如何用 C 實現上面論文思路, 用於實戰開發中.. 我這裡拋磚砸高鐵. -:
前言 - 結構介面先行
先看設計的數據結構
#ifndef _H_STREE #define _H_STREE typedef unsigned long long stree_key_t; typedef union { void * ptr; double number; signed long long i; unsigned long long u; } stree_value_t; struct stree { struct stree * left; // 左子樹 struct stree * right; // 右子樹 unsigned size; // 樹節點個數 stree_key_t key; // tree node key stree_value_t value; // tree node value }; typedef struct stree * stree_t; inline unsigned stree_size(const struct stree * const node) { return node ? node->size : 0; } #endif//_H_STREE
Size Balanced Tree 中多了一個特色節點 unsigned size; 用戶記錄當前樹上節點個數. 相比 red black tree
後者多記錄了 父親節點和紅黑性質. 每種平衡搜索樹, 都有自己的特殊欄位. 看的出後續核心操作都是
圍繞 unsigend size; 欄位.
(對於 key 和 value 設計持開放態度. 其中 key 是必須的, 不過這裡直接 unsigned long long 走起了)
首先看看最好理解的旋轉部分(出道就是巔峰), 的 rotate 旋轉操作
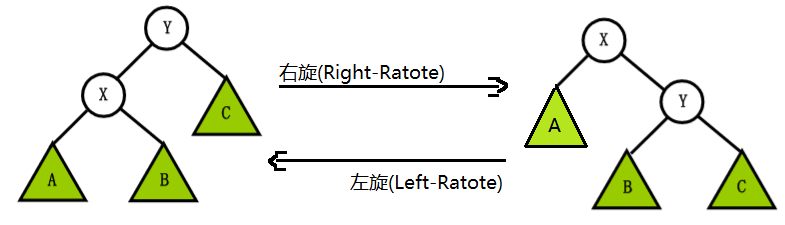
// stree_left_rotate - size tree left rotate static void stree_left_rotate(stree_t * pode) { stree_t node = *pode; stree_t right = node->right; node->right = right->left; right->left = node; right->size = node->size; node->size = stree_size(node->left) + stree_size(node->right) + 1; *pode = right; } // stree_right_rotate - size tree right rotate // // (y) left rotate (x) // / \ ------------> / \ // (x) [C] [A] (y) // / \ <------------ / \ // [A] [B] right rotate [B] [C] // static void stree_right_rotate(stree_t * pode) { stree_t node = *pode; stree_t left = node->left; node->left = left->right; left->right = node; left->size = node->size; node->size = stree_size(node->left) + stree_size(node->right) + 1; *pode = left; }
強烈好好看看練習練習, 否則後面更加不懂.
: ) 好想說, 後面不用看了, 複製我的代碼. 如果用的時候用吧, 否則就別再見了.
正文 - 有時候要認命
當前核心是翻譯論文, 並且終結 Size Balanced Tree 各種花式的代碼.
細節部分看論文, 看作者原文思路.這裡只是貼代碼, 帶你感受一下一個上的了臺面的 Size Balanced Tree 實現 ~
stree.h
#ifndef _H_STREE #define _H_STREE typedef unsigned long long stree_key_t; typedef union { void * ptr; double number; signed long long i; unsigned long long u; } stree_value_t; struct stree { struct stree * left; // 左子樹 struct stree * right; // 右子樹 unsigned size; // 樹節點個數 stree_key_t key; // tree node key stree_value_t value; // tree node value }; typedef struct stree * stree_t; inline unsigned stree_size(const struct stree * const node) { return node ? node->size : 0; } // // stree_delete - Size Balanced Tree delete destroy // poot : 指向 tree 對象指針 // return : void // extern void stree_delete(stree_t * poot); // // stree_insert - size tree insert node // poot : 指向 tree 對象指針 // key : 插入 node key // value : 插入 node value // return : void // extern void stree_insert(stree_t * poot, stree_key_t key, stree_value_t value); // // stree_remove - size tree remove node // poot : 指向 tree 對象指針 // key : 查找 node key // return : void // extern void stree_remove(stree_t * poot, stree_key_t key); // // stree_find - 尋找到指定的節點 // root : tree 對象 // key : 查找 node key // return : 查找 tree node, NULL 表示沒有 // extern stree_t stree_find(stree_t root, stree_key_t key); // // stree_rank - 返回 key 在 root 樹中排名, 也就是比 key 小的那顆樹的大小上加 1 // root : tree 對象 // key : 查找 node key // return : 排名 // extern unsigned stree_rank(stree_t root, stree_key_t key); // // stree_select - root 根節點樹種排名為 k 的節點 // root : tree 對象 // k : 排名 [1, stree_size(root)] // return : 返回查詢到節點 // extern stree_t stree_select(stree_t root, unsigned k); // // stree_pred - 查找 root 前驅節點, 比 key 小的最大的數 // root : tree 對象 // key : 查找 node key // return : 返回查詢到節點 // extern stree_t stree_pred(stree_t root, stree_key_t key); // // stree_succ - 查找 root 後繼節點, 比 key 大的最小的數 // root : tree 對象 // key : 查找 node key // return : 返回查詢到節點 // extern stree_t stree_succ(stree_t root, stree_key_t key); #endif//_H_STREE
上面 delete 和 remove 單詞和論文中比對有些不一樣. 因為在 C / C++ 中 delete 語義是銷毀.
所以採用 remove 去除的節點的語義單詞. 應該更加貼合實際開發的代碼函數定義.
stree.c
#include "stree.h" #include <stdlib.h> #include <stdbool.h> static void stree_free(stree_t root) { if (root->left) stree_free(root->left); if (root->right) stree_free(root->right); free(root); } // // stree_delete - Size Balanced Tree delete destroy // poot : 指向 tree 對象指針 // return : void // inline void stree_delete(stree_t * poot) { if (!poot || !*poot) return; stree_free(*poot); *poot = NULL; } // stree_left_rotate - size tree left rotate static void stree_left_rotate(stree_t * pode) { stree_t node = *pode; stree_t right = node->right; node->right = right->left; right->left = node; right->size = node->size; node->size = stree_size(node->left) + stree_size(node->right) + 1; *pode = right; } // stree_right_rotate - size tree right rotate // // (y) left rotate (x) // / \ ------------> / \ // (x) [C] [A] (y) // / \ <------------ / \ // [A] [B] right rotate [B] [C] // static void stree_right_rotate(stree_t * pode) { stree_t node = *pode; stree_t left = node->left; node->left = left->right; left->right = node; left->size = node->size; node->size = stree_size(node->left) + stree_size(node->right) + 1; *pode = left; } // stree_maintain - Size Balanced Tree Maintain static void stree_maintain(stree_t * pode, bool flag) { unsigned size; stree_t node = *pode; if (!node) return; if (!flag) { if (!node->left) return; size = stree_size(node->right); if (size < stree_size(node->left->left)) stree_right_rotate(pode); else if (size < stree_size(node->left->right)) { stree_left_rotate(&node->left); stree_right_rotate(pode); } else return; stree_maintain(&node->left, false); } else { if (!node->right) return; size = stree_size(node->left); if (size < stree_size(node->right->right)) stree_left_rotate(pode); else if (size < stree_size(node->right->left)) { stree_right_rotate(&node->right); stree_left_rotate(pode); } else return; stree_maintain(&node->right, true); } stree_maintain(pode, false); stree_maintain(pode, true); } static void stree_insert_node(stree_t * poot, stree_t node) { bool flag; stree_t root = *poot; if (!root) { (*poot = node)->size = 1; return; } ++root->size; // 插入到非空樹, 節點數加 1 if ((flag = node->key < root->key)) stree_insert_node(&root->left, node); else stree_insert_node(&root->right, node); stree_maintain(poot, !flag); } // // stree_insert - size tree insert node // poot : 指向 tree 對象指針 // key : 插入 node key // value : 插入 node value // return : void // inline void stree_insert(stree_t * poot, stree_key_t key, stree_value_t value) { stree_t node = calloc(1, sizeof(struct stree)); node->key = key; node->value = value; stree_insert_node(poot, node); } static stree_t stree_remove_node(stree_t * pode, const stree_key_t key, bool find) { stree_t record; stree_t node = *pode; if (!node) return NULL; if (find && !node->right) { // the right end node of right child tree replace the delete node *pode = node->left; return node; } if (!find && key == node->key) { if (node->size == 1) { // leaf node, need delete *pode = NULL; return node; } if (node->size == 2) { // single branch node, need child node replace delete node record = node->left ? node->left : node->right; node->left = node->right = NULL; } else { // max key node of left tree replace pnode record = stree_remove_node(&node->left, key, true); } if (record) { node->key = record->key; node->value = record->value; } --node->size; stree_maintain(pode, true); } else if (!find && key < node->key) { record = stree_remove_node(&node->left, key, false); if (record) --node->size; } else { record = stree_remove_node(&node->right, key, find); if (record) --node->size; } stree_maintain(pode, !find && key < node->key); return record; } // // stree_remove - size tree remove node // poot : 指向 tree 對象指針 // key : 查找 node key // return : void // inline void stree_remove(stree_t * poot, stree_key_t key) { stree_t node; if (!poot) return; node = stree_remove_node(poot, key, false); if (node) free(node); } // // stree_find - 尋找到指定的節點 // root : tree 對象 // key : 查找 node key // return : 查找 tree node, NULL 表示沒有 // stree_t stree_find(stree_t root, stree_key_t key) { while (root) { if (key < root->key) root = root->left; else if (root->key < key) root = root->right; else break; } return root; } // // stree_rank - 返回 key 在 root 樹中排名, 也就是比 key 小的那顆樹的大小上加 1 // root : tree 對象 // key : 查找 node key // return : 排名 // unsigned stree_rank(stree_t root, stree_key_t key) { int k = 0; while (root) { if (key < root->key) root = root->left; else if (root->key < key) { k += stree_size(root->left) + 1; root = root->right; } else { k += stree_size(root->left); break; } } return k; } // // stree_select - root 根節點樹種排名為 k 的節點 // root : tree 對象 // k : 排名 [1, stree_size(root)] // return : 返回查詢到節點 // stree_t stree_select(stree_t root, unsigned k) { while (root) { unsigned size = stree_size(root->left); if (k < size) root = root->left; else if (size < k) { root = root->right; k -= size + 1; } else break; } return root; } /* 前驅節點 1. 若一個節點有左子樹,那麼該節點的前驅節點是其左子樹中 key 值最大的節點 2. 若一個節點沒有左子樹,那麼判斷該節點和其父節點的關係 2.1 若該節點是其父節點的右孩子,那麼該節點的前驅節點即為其父節點。 2.2 若該節點是其父節點的左孩子,那麼需要沿著其父親節點一直向樹的頂端尋找, 直到找到一個節點P,P節點是其父節點Q的右孩子,那麼Q就是該節點的後繼節點 */ static stree_t stree_get_right(stree_t root) { if (root) { while (root->right) root = root->right; } return root; } static stree_t stree_get_right_p(stree_t root, stree_key_t key, stree_t * pq, stree_t * pr) { while (root) { if (key == root->key) return root; *pq = root; if (key < root->key) root = root->left; else { *pr = root; // 出現右拐點, 父節點 Q 的右孩子 root = root->right; } } return root; } // // stree_pred - 查找 root 前驅節點, 比 key 小的最大的數 // root : tree 對象 // key : 查找 node key // return : 返回查詢到節點 // stree_t stree_pred(stree_t root, stree_key_t key) { if (root) { stree_t q = NULL, r = NULL; stree_t p = stree_get_right_p(root, key, &q, &r); if (!p) return NULL; // 有左子樹 if (p->left) return stree_get_right(p->right); // 沒有前驅節點的情況 if ((!p) || (p && !r)) return NULL; // 沒有左子樹, 其父節點的右節點 if (p == q->right) return q; // 沒有左子樹, 是其父節點的左節點 return r; } return root; } /* 後繼節點 1. 若一個節點有右子樹,那麼該節點的後繼節點是其右子樹中 key 值最小的節點 2. 若一個節點沒有右子樹,那麼判斷該節點和其父節點的關係 2.1 若該節點是其父節點的左孩子,那麼該節點的後繼結點即為其父節點 2.2 若該節點是其父節點的右孩子,那麼需要沿著其父親節點一直向樹的頂端尋找, 直到找到一個節點P,P節點是其父節點Q的左孩子,那麼Q就是該節點的後繼節點 */ static stree_t stree_get_left(stree_t root) { if (root) { while (root->left) root = root->left; } return root; } static stree_t stree_get_left_p(stree_t root, stree_key_t key, stree_t * pq, stree_t * pr) { while (root) { if (root->key == key) return root; *pq = root; // 設置父親節點 if (root->key < key) root = root->right; else { *pr = root; // 出現左拐點, 父節點 Q 的左孩子 root = root->left; } } return root; } // // stree_succ - 查找 root 後繼節點, 比 key 大的最小的數 // root : tree 對象 // key : 查找 node key // return : 返回查詢到節點 // stree_t stree_succ(stree_t root, stree_key_t key) { if (root) { stree_t q = NULL, r = NULL; stree_t p = stree_get_left_p(root, key, &q, &r); if (!p) return NULL; // 有右子樹 if (p->right) return stree_get_right(p->right); // 沒有前驅節點的情況 if ((!p) || (p && !r)) return NULL; // 沒有右子樹, 其父節點的左節點 if (p == q->left) return q; // 沒有右子樹, 是其父節點的右節點 return r; } return root; }
這裡也簡單寫個測試例子, 保證核心邏輯插入和查找還有銷毀可以用.
main.c
#include <stdio.h> #include <stdlib.h> #include "stree.h" // // Size Balanced Tree // int main(int argc, char * argv[]) { stree_t root = NULL; // 插入數據 for (int i = 0; i < 9; i++) stree_insert(&root, i, (stree_value_t) { .i = i }); int key = 6; stree_t node = stree_find(root, key); if (NULL == node) { fprintf(stderr, "stree_find is error key = %d\n", key); exit(EXIT_FAILURE); } printf("key = %d, node = %lld\n", key, node->value.i); stree_remove(&root, key); node = stree_find(root, key); if (node) { fprintf(stderr, "stree_find is error key = %d\n", key); exit(EXIT_FAILURE); } printf("stree_remove is success key = %d\n", key); stree_delete(&root); return 0; }
論文 + C 代碼互相配合, 希望能對準備嘗試的人有些作用. 長舒一口氣.
拋開圖, 面試最難不過二叉樹 ~,~
開發中 tree set hash list vector 非常常見, 其中 tree 常被 hash 和 set 搶掉運用場景. 例如 id 管理.
但二叉樹是批量搜索業務的基石 (別說跳錶). 不管如何你都得嘗試躍遷過 ~-~
後記 - 開心就好
錯誤是難免的, 歡迎交流指正, 互相提升 ~
負け犬達のレクイエム - http://music.163.com/m/song?id=29751658&userid=16529894

: )
故事的開頭,總是驚鴻一瞥,一眼千年,故事的結尾,總是瀟灑轉身,漸行漸遠
-:



