本文介紹整數編碼,主要討論無符號整數和有符號整數的編碼不同所帶來的一些理解上的問題。無符號整數編碼很容易理解,因其沒有符號位,在二進位無符號整數轉為十進位數時,每一位上的數字(0或1)乘以該為的權值2w-1(w從1開始),然後相加即可。對於有符號整數,最高位為符號位,符號位的權值決定了正負。有符號整 ...
本文介紹整數編碼,主要討論無符號整數和有符號整數的編碼不同所帶來的一些理解上的問題。無符號整數編碼很容易理解,因其沒有符號位,在二進位無符號整數轉為十進位數時,每一位上的數字(0或1)乘以該為的權值2w-1(w從1開始),然後相加即可。對於有符號整數,最高位為符號位,符號位的權值決定了正負。有符號整數編碼有原碼、反碼和補碼三種方式。
1、原碼和反碼
原碼的最高有效位是符號位,用來確定剩下的位應該取正權還是負權,表示如下:
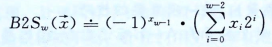
反碼的最高有效位的權值為-(2w-1-1),反碼表示如下:

但是這兩種編碼對於0的編碼都存在兩種不同的編碼方式,[00...0]解釋為+0,而值-0在原碼中表示為[10...0],在反碼中表示為[11...1]。所以幾乎所有的現在機器都使用補碼來表示有符號整數。
2、補碼
補碼的最高有效位的權值為-2w-1,補碼表示為:
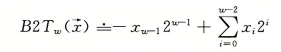
對於0值,補碼也是唯一 的編碼[00...0]。以char型的有符號整數舉例補碼編碼:
| 十進位 | 二進位 |
| 1 | 00000001 |
| 0 | 00000000 |
| -1 | 11111111 |
3、有符號整數與無符號整數之間的轉換
轉換過程中二進位編碼是不變的,也就是二進位中的每一位(0或1)是不變的,變的是計算的方式,例如:
無符號轉為有符號:unsigned char x = 255,則(char)x的值為-1。
有符號轉為無符號:char x = -127,則(unsigned char)x的值為129。
4、擴展一個整數的位表示
擴展一個整數的位時,要保證擴展之後的數與原數值相等。
- 無符號整數的零擴展:
對於無符號整數,擴展之後,在高位加0,例如八位二進位數[01000001]擴展為十六位時的表示為[0000 0000 0100 0001],高位全部為0。
- 有符號整數(補碼)的符號位擴展:
對於有符號整數,符號位為正的,則高位全部為0,符號位為負的,高位全部為1。例如八位二進位數[1000 0001](十進位為-127)擴展為十六位時的表示為[1111 1111 1000 0001](十進位為-127),八位二進位數[0000 0001]擴展為十六位時的表示為[0000 0000 0000 0001]。
5、截斷一個整數的位表示
對於無符號整數的截斷很好理解,截斷後的各位按照無符號編碼進行計算,肯定為一個正整數。但是對於一個有符號整數的截斷,則可能出現截斷後,符號翻轉的情況,因為截斷後的最高有效位為0還是1來決定正負。
6、關於有符號整數與無符號整數的思考
由於編碼的原因,很多時候考慮不周全就會出現意外情況,在擴展位或截斷位以及強制轉換的過程中,都需要仔細考慮各種情況。並且在整數運算的時候需要考慮溢出的情況,不同位數(char,short,int)的整數之間的混合運算和有符號與無符號的混合運算的情況。後兩種情況的規則如下:
- 不同位數的整數之間混合運算時,需要首先將位數低的整數強制轉換為位數高的整數,再進行運算
- 有符號與無符號整數之間的運算時,需要首先將有符號數轉換為無符號數,再進行運算



