因為ECMAscript中所有數值都是以IEEE-75464格式存儲,所以才會誕生了位操作符的概念. 位操作符作用於最基本的層次上,因為數值按位存儲,所以位操作符的作用也就是操作數值的位.不過位操作符並不能操作64位的值.所以位操作符會先將64位的值轉換成32位的值,然後執行操作,最後再將結果轉換成 ...
因為ECMAscript中所有數值都是以IEEE-75464格式存儲,所以才會誕生了位操作符的概念.
位操作符作用於最基本的層次上,因為數值按位存儲,所以位操作符的作用也就是操作數值的位.不過位操作符並不能操作64位的值.所以位操作符會先將64位的值轉換成32位的值,然後執行操作,最後再將結果轉換成64位的值.
但對於開發人員來說,這整個過程就像是只存在32位的數值一樣,這是因為64位存儲格式是透明的.
當然這裡所說的數值指的是整數.在對於有符號的整數中,32位的前31位用於表示整數的值,而第32位則表示整數的符號(即0表示正數,1表示負數),我們把這第32個表示符號的位叫做符號位,符號位也決定了其它位的數值的格式.
正數都是按純二進位格式存儲的,在前31位中的每一個位都表示2的冪.即第一位表示2^0(2的零次方),第二位表示2^1(2的1次方),依次類推.第一位也叫做位0,後面依次類推,第32位就叫做位31,其它沒有用到的位都以0填充,也可以被忽略不計.
比如十進位整數10的二進位表示是0000 0000 0000 0000 0000 0000 0000 1010或者更簡單的1010..這是4個有效位,這4位就決定了實際的值.我們可以用toString()方法指定參數可以表示將一個十進位數轉換成二進位數.所以我在這裡寫了一個函數,表示將一個十進位數轉換成二進位數,如下圖所示:
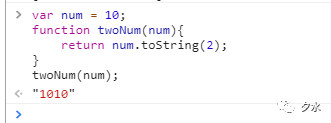
既然二進位數1010就是十進位數10,那麼我們還可以將這個二進位數轉換成十進位數,是如何計算的呢?很簡單,因為二進位數最後一位表示符號,所以不計,這裡的101各代表冪數為3,2,1,這也是為什麼十進位轉換成二進位數要取餘數倒排的原因,然後將位上的數乘以基數2的冪數.也就是說可以寫成等式2^3x1 + 2^2 x 0 + 2^1 x 1 = 10.(2^*表示2的*次方).
負數同樣以二進位碼存儲,只不過與正數有點區別,區別就是負數的格式是二進位補碼.在求二進位補碼的時候,有以下三個規則:
(1).先求出這個負數的絕對值的二進位碼.比如十進位數-17,就是先求17的二進位碼.
(2).然後求二進位碼的反碼,就是將0變成1,1變成0.
(3)最後將得到的二進位反碼加1.
比如說求十進位數-10的二進位碼,我們要先求10的二進位碼,也就是
0000 0000 0000 0000 0000 0000 0000 1010,然後取反碼就是
1111 1111 1111 1111 1111 1111 1111 0101,最後加1,但因為二進位數只能是1或者0表示,所以1+1大於2的話,就會向前進位1.所以這個反碼加1最後得到的值應該是1111 1111 1111 1111 1111 1111 1111 0110.而這個也是-10的二進位表示.需要註意的是在處理有符號的整數的時候,是訪問不到第32位的(也就是位31).
但在實際情況中,ECMAscript是會儘力向我們隱藏所有的這些信息.也就是說在實際轉換負數的二進位碼時,它只會將這個負數的絕對值的二進位碼前面加上一個負號,就表示這個負數的二進位碼.如下圖所示:
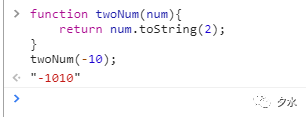
這個轉換過程說明ECMAscript解析引擎理解了二進位補碼並將其以更合乎邏輯的形式展示出來.
在預設情況下,ECMAscript中的所有整數都是有符號整數.當然也存在無符號整數,對於無符號的整數來說,第32位不會再表示符號,因為無符號整數只能是正整數.而且無符號整數的值可以更大,因為第32位不再表示符號,而可以表示成數值.什麼意思呢?就是說當我們再將十進位數轉換成二進位數時,必須要除到商為0時,才會倒排餘數,而第32位恰好就是商為0的那個餘數.而正整數值越大,我們可以省略的有效位數就越多,此時值也就越大.
在ECMAscript中,當對數值應用位操作符的時候,雖然後臺會發生將64位數值轉換成32位數值,然後執行完操作之後,再轉換成64位的數值這個轉換過程.但正因為這個轉換過程導致了一個嚴重的副效應,也就是說在對特殊的NaN和Infinity值應用位操作符時,這兩個值會被當成0來處理.
而如果對非數值應用位操作符,會自動使用Number()函數將其轉換成一個數值來操作,然後再應用位操作符,得到的結果也將是一個數值.
總的說來,位操作符主要包含按位非(NOT),按位與(AND),按位或(OR),按位異或(XOR),左移,無符號右移和有符號右移7個操作符.接下來,咱們就來一一分析這7個操作符.
a.按位非(NOT):按位非用一個波浪線符號"~"表示,執行按位非的結果就是取得數值的反碼.它也是ECMAscript中少數幾個與二進位計算相關的操作符.
比如求10的按位非結果,那麼按照求二進位得到10的二進位碼是0000 0000 0000 0000 0000 0000 0000 1010,然後取反碼就是1111 1111 1111 1111 1111 1111 1111 0101.而要將這個反碼轉換成十進位數,還需要以下過程:
此時,位31上的1代表符號為負,因為負數的補碼就是反碼加1,所以得知負數的反碼就等於補碼減1,所以此時求得負數的反碼是1111 1111 1111 1111 1111 1111 1111 0100,所以負數的原碼就是取反,變成了0000 0000 0000 0000 0000 0000 0000 1011,所以此時再將這個二進位數轉換成十進位數就是-(2^3 * 1+2^2 * 0+2^1 * 1 + 2^0 * 1)=-11.要理清這個轉換過程,需要知道什麼是反碼,什麼是原碼,什麼又是補碼,因為參與計算的是補碼,而要轉換的是求原碼.也就是說,要想將二進位反碼轉換成十進位數,就必須求得二進位反碼的原碼,然後對原碼直接按照二進位轉換成十進位的方式來計算轉換.現在我們來驗證一下是否是我們所想的,如下圖所示:

再比如求-10的按位非結果,按照理論分析,我們從前述可以得知最終-10的二進位碼為1111 1111 1111 1111 1111 1111 1111 0110,取反碼就變成了0000 0000 0000 0000 0000 0000 0000 1001,而此時的二進位反碼的補碼,原碼都一樣,所以直接計算就是2^3*1+2^2*0+2^1*0+2^0*1=9.如下圖所示:

通過以上示例還應該得到一個結論:正整數的二進位碼的反碼與原碼補碼不一致,而負整數的二進位碼的反碼就與原碼補碼一致.換句話說,就是正數的原碼與補碼一樣,負數的原碼與補碼不一樣.
如果實在是不能理解原碼,補碼與反碼,可以直接把這個操作符理解為數值加1取反.如10加1取反就變成-11,-10加1取反就變成9.
而實際上,對按位非的結果比如~10與~-10,我們還可以寫成如下圖所示的表示:
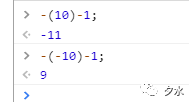
我們可以用變數來表示,如下圖所示:

雖然不用按位非操作符的以上所表示的代碼也能輸出同樣的結果,但由於按位非是對底層進行操作,所以使用按位非操作符的速度會更快.
b.按位與(AND)
按位與操作符用一個和號字元(&)表示,它有兩個操作數,從本質上講,按位與操作就是將數值的每一位二進位碼對齊,然後根據以下規則,對相同為止上的兩個數執行AND操作.規則如下:
第一個數值的位 第二個數值的位 結果
1 1 1
1 0 0
0 1 0
0 0 0
簡而言之,就是只在兩個數值的位數都對應為1的時候,結果才為1,任何一位是0,結果都是0.
如以下示例:
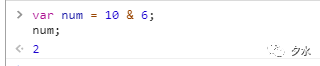
對10和6進行按位與操作時返回2,這是為什麼呢?請看底層原理:
首先10轉換成二進位數就是0000 0000 0000 0000 0000 0000 0000 1010,而6轉換成二進位數則是0000 0000 0000 0000 0000 0000 0000 0110.過程可以如下:
10 = 0000 0000 0000 0000 0000 0000 0000 1010
6 = 0000 0000 0000 0000 0000 0000 0000 0110
AND = 0000 0000 0000 0000 0000 0000 0000 0010
然後按位與結果轉換成十進位數就是2^1*1 = 2.
所以最終結果為2.
再比如求2&5的結果,現在咱們按照步驟來計算出結果,然後再驗證答案對不對.
首先求得2的二進位數為0000 0000 0000 0000 0000 0000 0000 0010,5的二進位數為0000 0000 0000 0000 0000 0000 0000 0101.
2 = 0000 0000 0000 0000 0000 0000 0000 0010
5 = 0000 0000 0000 0000 0000 0000 0000 0101
AND = 0000 0000 0000 0000 0000 0000 0000 0000
而這個結果轉換成十進位數就是0.
所以得出結果是0,現在咱們來驗證一下,如下圖所示:

c.按位或(OR)
按位或操作符由一個豎線符號(|)表示,同樣也有兩個操作數.從本質上講,也可以說是將數值的二進位碼對齊,但與按位與操作符有一點點區別,就是它的規則與按位與操作符不一樣,具體如下:
第一個數值的位 第二個數值的位 結果
1 1 1
1 0 1
0 1 1
0 0 0
簡而言之,就是按位或操作符只有其對應的兩個位都是0的情況下才是0,其它有一個位是1的情況下都是1.如以下示例:

現在,我們就來分析一下為什麼結果是7,其實與按位與的底層操作很相似,2和5的二進位數前述示例已求得:
2 = 0000 0000 0000 0000 0000 0000 0000 0010
5 = 0000 0000 0000 0000 0000 0000 0000 0101
OR = 0000 0000 0000 0000 0000 0000 0000 0111
而將按位或的結果轉換成十進位數就是2^2*1 + 2^1*1 + 2^0*1 = 7.
所以結果7就是這麼求來的.
d.按位異或(XOR)
按位異或操作符由一個插入符號(^)表示,也有兩個操作數,其本質也與按位與和按位或操作符相同,但其規則也不一樣,如下:
第一個數值的位 第二個數值的位 結果
1 1 0
1 0 1
0 1 1
0 0 0
也就是說,按位異或操作符只有在其中一個位為1時才返回1,否則就是0.
如對2^5求結果如下圖:

現在來分析一下為什麼結果是7,過程也與求按位與和按位或結果一致.
2 = 0000 0000 0000 0000 0000 0000 0000 0010
5 = 0000 0000 0000 0000 0000 0000 0000 0101
XOR = 0000 0000 0000 0000 0000 0000 0000 0111
這裡因為對應位沒有變化,所以最終結果才會和按位或結果一致.
e.左移
左移操作符由兩個小於號(<<)表示,也是兩個操作數,第一個操作數就表示要左移的數值,第二個操作數表示左移的位數.所以左移操作符的含義就是將數值的所有位向左移動指定的位數.
而在向左移動了指定的左移位數之後,原數值的右側會多出指定的位數個空位(比如指定左移4位,也就多出4個空位,依次類推)出來,不過左移操作會自動以0來填充這些空位.
如以下示例:

現在來分析一下為什麼結果是40,首先5的二進位數是
0000 0000 0000 0000 0000 0000 0000 0101,指定的是向左移動3位,所以整體向左移動3位,就變成了0000 0000 0000 0000 0000 0000 0010 1000,而這個二進位轉換成十進位數就是2^5*1 + 2^3*1 = 40.
所以最終結果就是40.
註意,左移操作並不會影響操作數的符號位,換句話說,如果將-5左移3位,結果將是-40,而不是40.
f.右移操作符.
右移操作符又分為無符號右移和有符號右移操作符.
(1).有符號的右移操作符.
有符號的右移操作符由兩個大於符號表示(>>),這個操作符的含義就是將數值的位向右移指定的位數,同時保留符號位的值(正負號標記),有符號的右移操作符與左移操作符剛好相反,比如40向右移動3位就是5.
同樣的,在移位的過程中,也會出現空位,而這時候,ECMAscript會用符號位的值來填充所有空位,也就是說每向右移動一位,移走的位上的數不管是1,還是0都會消失了,則會在數值的左側補充一位,而這位的值就是符號位的值,即如果是正數,補充0,負數補充1.
如以下一個示例:
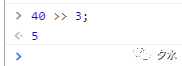
現在,咱們就來分析分析為什麼最終結果為0.首先由前述可以得知40的二進位數為0000 0000 0000 0000 0000 0000 0010 1000,指定的是向右移動3位,那麼整體向右移就變成了0000 0000 0000 0000 0000 0000 0000 0101,這個轉換成十進位數也就是5.所以才會說有符號的右移與左移結果相反.
再來看一個示例:

現在,咱們就來分析分析為什麼最終結果為0.首先由前述可以得知5的二進位數為0000 0000 0000 0000 0000 0000 0000 0101,指定的是向右移動3位,那麼整體向右移3位,左側就要補充符號位的值,因為是正數(正數符號表示為0),所以補充3個0,就變成了
0000 0000 0000 0000 0000 0000 0000 0000.所以最終結果為0.
如果這樣不能理解的話,那麼假設向右移動一位,也就是求5 >> 1的結果,同樣在最左側補充一個符號位的值0,右移走了末位的1.所以變成了0000 0000 0000 0000 0000 0000 0000 0010.這個轉換成十進位數就是2.現在咱們來操作驗證一下,如下圖:

(2).無符號右移操作符.
無符號右移操作符由三個大於符號表示(>>>).這個操作符也是會將所有的32位都整體向右移動指定的位數.對於正數來說,其實無符號右移操作符和有符號右移操作符的結果一致.
如5 >>> 1仍然是2,按照同樣的過程步驟分析.
對於正數沒有什麼變化,但對於負數來說,變化可就大了,首先無符號右移操作符是以0填充空位,而不是像有符號右移操作符那樣以符號位的值填充.所以才會正數與有符號右移操作符的結果相同.但是負數就不一樣了,無符號右移操作符會把負數的二進位碼當成正數的二進位碼,而且負數是由其絕對值的二進位補碼表示,因此導致無符號右移之後結果會很大.換句話說,就是對負數進行無符號右移操作時只會返回正數.
如求-5 >>> 3.我們先自己求一遍,首先-5的二進位補碼為1111 1111 1111 1111 1111 1111 1111 1010,而因為無符號右移會把這個補碼當成正數的二進位碼,所以轉換成十進位數就是(口算不太現實,太大了,還是讓電腦來算吧)如下圖所示:

所以就會被當成4294967290,然後這個正數的二進位碼右移3位變成了0001 1111 1111 1111 1111 1111 1111 1111,轉換成十進位數就是如下圖所示:

所以最終結果就是536870911.
現在,我們來驗證一下,如下圖所示:
知道了位操作符之後,現在咱們來分析一道題,有這樣一道前端面試題,寫一個函數用於判斷一個非負整數是否是2的非負整數次冪.而有人曾經這樣寫,如下圖所示:
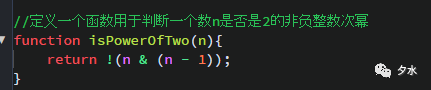
那麼為什麼這樣寫呢,我們來分析一下這其中原理,首先什麼是函數,使用function關鍵字聲明的都可以被叫做函數,而這裡定義的函數名也比較語義化,叫做isPowerOfTwo,圓括弧中的n叫做函數的參數,顧名思義,這裡的參數就是傳入一個非負整數.而這個函數的作用就是要判斷傳入的參數(即非負整數)是否是2的非負整數次冪.
return也是一個關鍵字,表示返回一個值,用在函數當中,而要記住的是,如果在函數當中寫入了return關鍵字,在這個關鍵字表示的語句結束後面再寫其它語句是沒有效果的,如下圖所示:
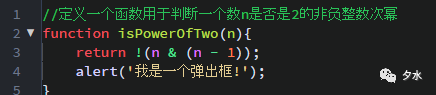
如上圖所示,alert()方法表示彈出一個原生的彈出框,但實際上在調用這個定義的判斷函數之後,是不會執行彈出框的,這就是return關鍵字在這裡起到的作用.
現在再來分析一下裡面的結構,嘆號(!)也就是邏輯非的意思,這個操作符會把一個操作數轉換成布爾值,然後取反.
再來看圓括弧裡面的和字元號&,在學了位操作符之後,我們就應該知道這個符號就是按位與的意思,而按位與是操作二進位數的位的,對應規則也應該知道,就是當兩個操作數(在這裡指n和n-1)的對應位都是1時,最終返回的對應位結果才是1,否則就是0.按位與的作用就是將位對齊.所以,在返回這個結果之前,我們還需要知道如何轉換成二進位數.
我們應該知道對象的toString()方法,可以為其指定一個參數為基數2,就可以將一個操作數轉換成二進位數返回,當然這裡也是返回一個字元串.而為了方便,我將這個方法封裝在一個函數中,如下圖所示:
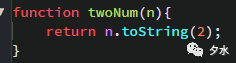
現在我們再來看看一個非負整數如果是2的冪,會有什麼特點,我們可以調用以上的定義函數將一個非負整數轉換成二進位數,而一個非負整數如果是2的冪,我們應該知道2的冪有2^0 = 1,2^1 = 2,2^2 = 4......依次類推,我們從而得知1,2,4,8,16....等就是2的冪,而我們將這些值轉換成二進位數,就可以知道有什麼樣的關係了,比如1轉換成二進位就是1,2轉換成二進位是10,4轉換成二進位是100......依此類推,不信咱們可以用上面定義好的函數來驗證,如下圖:
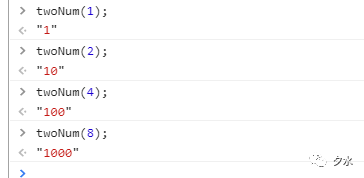
現在我們就應該知道規律了,如果一個非負整數是2的非負整數次冪的話,那麼這個數一定是上一個2的非負整數次冪的二進位數左移了一位.而通過之前知道的左移操作符,我們知道,左移就是將位往左移動一位,然後在移動後的空位中以0填充.
現在,我們再來看看n-1,假設是2的非負整數次冪的非負整數,減1,然後再將其轉換成二進位數,比如1是2的非負整數次冪,1-1 =0.轉換成二進位就是0(這裡是簡寫),再比如2-1=1的二進位就是1,4-1=3的二進位就是11,7就是111.不信我們可以通過以上定義的函數來驗證,如下圖所示:
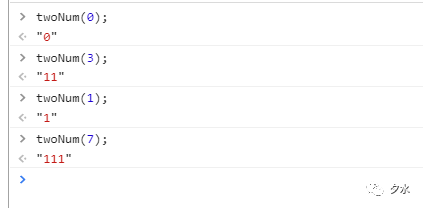
通過使用按位與操作符取得非負整數與非負整數減1的結果,不言而喻,始終都會返回0,為什麼呢?因為對應位的關係,我們取其中一個為例子,如下:
0 = 0000 0000 0000 0000 0000 0000 0000 0000
1 = 0000 0000 0000 0000 0000 0000 0000 0001
AND = 0000 0000 0000 0000 0000 0000 0000 0000
所以最終結果就是二進位數0000 0000 0000 0000 0000 0000 0000 0000,轉換成十進位數就是0.
這樣,我們就應該知道了,如果這個非負整數是2的非負整數次冪的話,那麼它與它減1兩個操作數取按位與結果就應該是0.
而我們知道邏輯非操作符對數值0會返回true的布爾值,所以當如果傳入的參數是非負整數,並且還是2的非負整數次冪的話,那麼這個函數最終就會返回true.我們可以直接調用這個函數,如下圖所示:
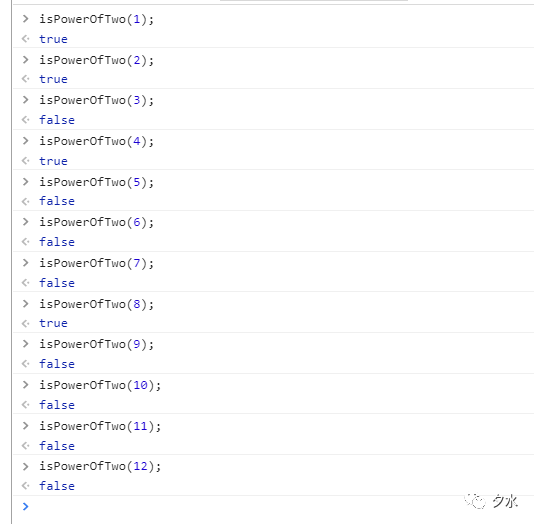
這麼一個小小的前端面試題卻涉及到這麼多的知識點,可想而知原生js在前端當中的重要性了.



