Description 給出a,b,c,x1,x2,y1,y2,求滿足ax+by+c=0,且x∈[x1,x2],y∈[y1,y2]的整數解有多少對? 給出a,b,c,x1,x2,y1,y2,求滿足ax+by+c=0,且x∈[x1,x2],y∈[y1,y2]的整數解有多少對? Input 第一行包含7 ...
Submit: 140 Solved: 48
[Submit][Status][Discuss]
Description
給出a,b,c,x1,x2,y1,y2,求滿足ax+by+c=0,且x∈[x1,x2],y∈[y1,y2]的整數解有多少對?
Input
第一行包含7個整數,a,b,c,x1,x2,y1,y2,整數間用空格隔開。 a,b,c,x1,x2,y1,y2的絕對值不超過10^8。
Output
輸出整數解有多少對?
Sample Input
1 1 -3 0 4 0 4Sample Output
4HINT
Source
一眼就能看出是擴歐 利用擴歐的通項公式求出上下邊界進行處理 註意特殊情況的判斷 註意這裡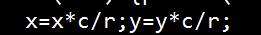
一定要先乘再除
mmp調了一晚上拍了n組數據都沒拍出錯誤來。。
#include<iostream> #include<cstdio> #include<cmath> #define LL long long using namespace std; const LL MAXN=1e6+10; LL a,b,c,x1,x2,yy1,y2,x,y; LL exgcd(LL a,LL b,LL &x,LL &y) { if(b==0){x=1,y=0;return a;} LL r=exgcd(b,a%b,x,y),tmp; tmp=x,x=y,y=tmp-a/b*y; return r; } LL min(LL a,LL b){return a<b?a:b;} LL max(LL a,LL b){return a>b?a:b;} int main() { cin>>a>>b>>c>>x1>>x2>>yy1>>y2;c=-c; if(a==0&&b==0) { if(c==0) {printf("%lld",(LL)(x2-x1+1)*(y2-yy1+1));return 0;} else {printf("0");return 0;} } if(a==0){ if(c%b) {printf("0");return 0;} if(c/b>=yy1&&c/b<=y2) {printf("%lld",x2-x1+1);return 0;} else {printf("0");return 0;} } if(b==0) { if(c%a) {printf("0");return 0;} if(c/a>=x1&&c/a<=x2) {printf("%lld",y2-yy1+1);return 0;} else {printf("0");return 0;} } LL r=exgcd(a,b,x,y); b=b/r;a=-a/r;//利用公式構造增量 if(c%r) {printf("0");return 0;} x=x*c/r;y=y*c/r; LL xlower,xupper,ylower,yupper; if(b>0) xlower=ceil( (double)(x1-x)/b ) , xupper=floor( (double)(x2-x)/b ); if(b<0) xlower=ceil( (double)(x2-x)/b ) , xupper=floor( (double)(x1-x)/b ); if(a>0) ylower=ceil( (double)(yy1-y)/a ) , yupper=floor( (double)(y2-y)/a ); if(a<0) ylower=ceil( (double)(y2-y)/a ) , yupper=floor( (double)(yy1-y)/a ); LL ans=max(0, min(xupper,yupper) - max(xlower,ylower) + 1 ); printf("%lld",ans); return 0; } //1 5 -3 -123 40 -567 41



