相關介紹: 二叉樹的三種遍歷方式(先序遍歷,中序遍歷,後序遍歷)的非遞歸實現,雖然遞歸方式的實現較為簡單且易於理解,但是由於遞歸方式的實現受其遞歸調用棧的深度的限制,當遞歸調用的深度超過限制的時候,會出現拋出異常的情況。為此,通過顯示的使用棧的方式來實現二叉樹遍歷的非遞歸方式,其在使用上 ...
相關介紹:
二叉樹的三種遍歷方式(先序遍歷,中序遍歷,後序遍歷)的非遞歸實現,雖然遞歸方式的實現較為簡單且易於理解,但是由於遞歸方式的實現受其遞歸調用棧的深度的限制,當遞歸調用的深度超過限制的時候,會出現拋出異常的情況。為此,通過顯示的使用棧的方式來實現二叉樹遍歷的非遞歸方式,其在使用上會更加的靈活。
運用下圖對二叉樹的三種遍歷方式進行介紹:

後序遍歷:
所謂的後序遍歷是指對一棵二叉樹按照左子樹,右子樹,根節點的順序遞歸的在一棵二叉樹的左右子樹中訪問相關節點的方式。如圖1.1所示的一棵二叉樹,其後序遍歷的結果為DEBCA
實現非遞歸方式的後序遍歷,有兩種。
第一種:
使用兩個棧來進行實現。註意到,後序遍歷可以看做以下遍歷過程的逆過程:先遍歷某個節點,然後遍歷其右孩子節點,再遍歷其左孩子節點,該過程的逆過程,即為後序遍歷的遍歷過程。如圖:
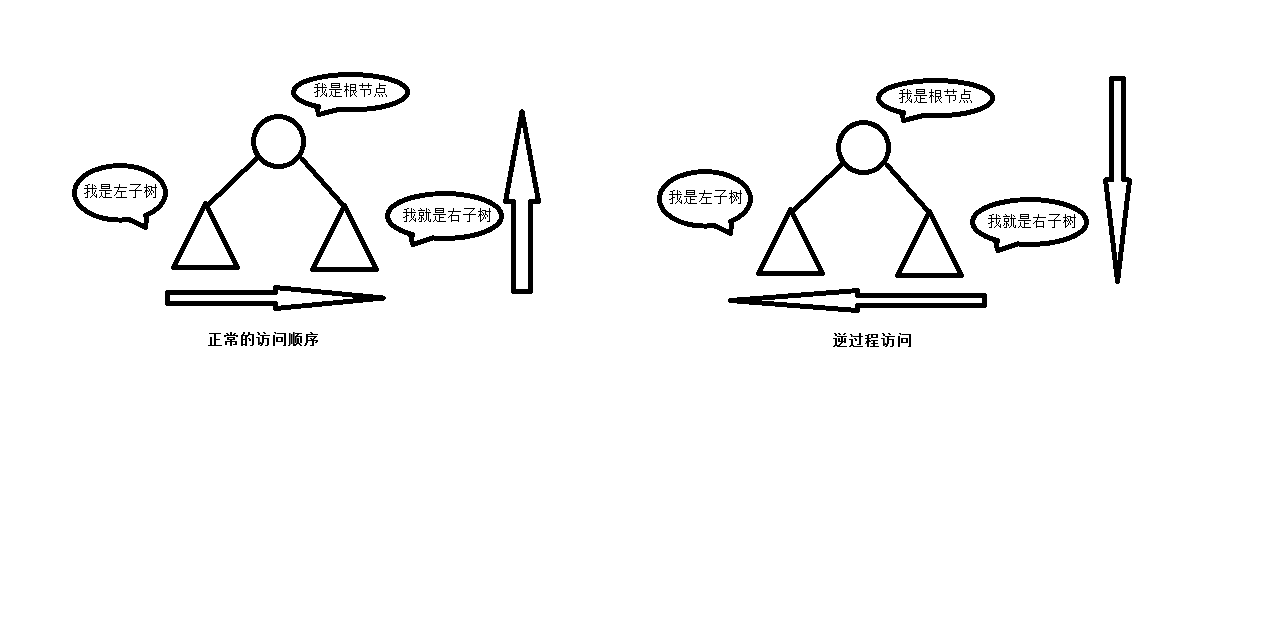
為此,我們可以按照如下的演算法得到二叉樹的後序遍歷結果:
- 初始化兩個棧,一個用於保存中間遍歷過程稱為棧s,一個用於保存最終的結果稱為棧output
- push根節點到第一個棧s中
- 從第一個棧s中pop出一節點,並將其push到第二個棧output中
- 將第一個棧s中pop出的節點的孩子節點,按左孩子,右孩子的順序push到第一個棧s中
- 重覆步驟3和4直到棧s為空
- 棧s為空時,所有節點都已push到棧output中,且按後序遍歷順序存放,依次將棧output的節點pop出併進行訪問,即為二叉樹後序遍歷的結果
以圖1.1為例,其過程如下:
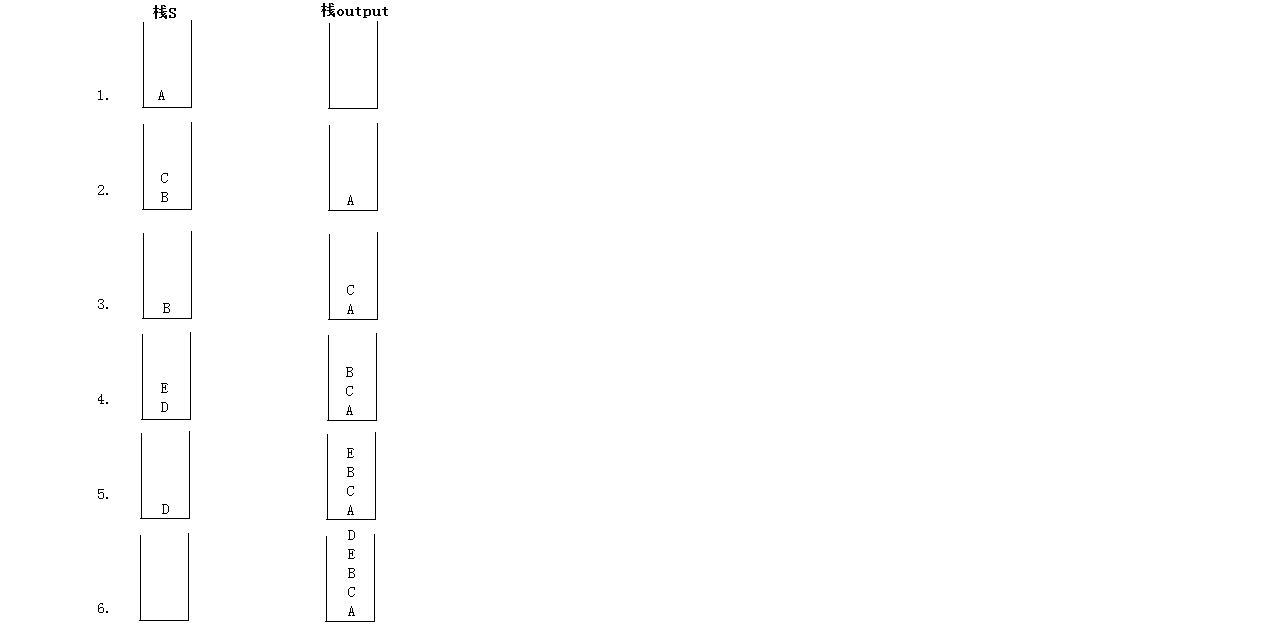
示例代碼如下:
/**
* 用於實現二叉樹的非遞歸方式的後序遍歷,方式1
* @param root 二叉樹的根節點
*/
public void PostRootTraverse(BinaryTreeNode root)
{
BinaryTreeNode T=root;
Stack s=new Stack();
Stack output=new Stack();
s.push(root);
//用於執行壓入棧的過程
while(!s.isEmpty())
{
T=s.pop();
output.push(T);
if(T.leftChild!=null)
s.push(T.leftChild);
if(T.rightChild!=null)
s.push(T.rightChild);
}
//用於執行對遍歷結果的每個節點的訪問過程
while(!output.isEmpty())
{
System.out.println(((BinaryTreeNode)output.pop()).data);
}
}第二種:
使用一個棧來進行實現,在搜索遍歷的過程中,從二叉樹的根節點出發,沿著該節點的左子樹向下搜索,在搜索的過程中每遇到一個節點判斷該節點是否是第一次經過,若是,則不立即訪問,而是將該節點入棧保存,遍歷該節點的左子樹。當左子樹遍歷完畢後再返回該節點,這時還不能立即訪問該節點,而是應當繼續進入該節點的右子樹進行遍歷,當左右子樹均遍歷完畢後,才能從棧頂彈出該節點並訪問它。由於在決定棧頂節點是否能訪問時,需要知道該節點的右子樹是否已經被遍歷完畢。因此,為解決這個問題,在演算法中還應當引入一個布爾型的訪問標誌變數flag和一個節點指針p。其中flag用來標誌當前棧頂節點是否被訪問過,當值為true的時候,表示棧頂節點已被訪問過,當值為false的時候,表示當前棧頂節點未被訪問過,指針p指向當前遍歷過程中最後一個訪問的節點。若當前棧頂節點的右孩子節點是空,或者就是p指向的節點,則表明當前節點的右子樹已遍歷完畢,此時就可以訪問當前棧頂節點。其操作的實現過程描述如下:
- 創建一個棧對象,根節點進棧,p賦初始化值為null
- 若棧非空,則棧頂節點的非空左孩子相繼進棧
- 若棧非空,查看棧頂節點,若棧頂節點的右孩子為空,或者與p相等,則將棧頂節點彈出棧並訪問它,同時使p指向該節點,並置flag為true,否則,將棧頂節點的右孩子壓入棧,並置flag的值為false
- 若flag值為true,則重覆執行步驟3。否則,重覆執行步驟2和3,直到棧為空為止。
示例代碼如下:
package queueandstack;
import java.util.Stack;
/**
* 用於演示二叉樹的遍歷的三種方式的代碼
* @author 學徒
*
*/
public class AroundTree
{
/**
* 用於實現二叉樹的非遞歸方式的後序遍歷,方式2
* @param root 二叉樹的根節點
*/
public void PostRootTraverse(BinaryTreeNode root)
{
BinaryTreeNode T=root;
if(T!=null)
{
Stack s=new Stack();
s.push(T);//根節點進棧
boolean flag;//訪問標記
BinaryTreeNode p=null;//p指向剛被訪問的節點
while(!s.isEmpty())
{
while(s.peek()!=null)//將棧頂節點的左孩子相繼入棧
{
s.push(((BinaryTreeNode)s.peek()).leftChild);
}
s.pop();//空節點退棧
}
while(!s.isEmpty())
{
T=(BinaryTreeNode)s.peek();//查看棧頂元素
if(T.rightChild==null||T.rightChild==p)
{
System.out.println(T.data);//訪問節點
s.pop();//移除棧頂元素
p=T;//p指向剛被訪問過的節點
flag=true;//設置訪問標記
}
else
{
s.push(T.rightChild);//右孩子節點入棧
flag=false;//設置未被訪問標記
}
if(!flag)
break;
}
}
}
}先序遍歷:
所謂的先序遍歷,是指對一棵二叉樹按照根節點,左子樹,右子樹的順序遞歸的在一棵二叉樹中的左右子樹中訪問相關節點的方式。如圖1.1所示的一棵二叉樹,其先序遍歷的結果是ABDEC
實現非遞歸方式的先序遍歷,有兩種。
第一種:
註意到,先序遍歷的過程為“根左右”,後序遍歷的過程為“左右根”,其後序遍歷的逆過程為“根右左”,其後序遍歷過程可以採用兩個棧形式來進行實現,實現的過程中,第一個棧存放當前節點的左孩子節點和右孩子節點,而其得到的出棧結果為“根右左”,為此,我們只需要將入第一個棧的節點順序調換以下(即先入右節點,再入左節點)即可得到“根左右”的出棧順序,其具體步驟如下描述:
- 初始化一個棧和一個隊列
- push根節點入棧
- 從該棧中pop出其一節點,並將該節點加入到隊列中
- 將該棧中pop出的節點的孩子節點,按照右孩子和左孩子的順序push到該棧中
- 重覆步驟2和步驟3直至棧為空
- 完成之後,所有的節點都push到該隊列中,且按先序遍歷的方式順序存放,直接pop出隊列中的節點,即為二叉樹的先序遍歷結果。
以圖1.1為例,其過程如下:

示意代碼如下:
/**
* 用於實現二叉樹的非遞歸方式的先序遍歷,方式1
* @param root 二叉樹的根節點
*/
public void PreRootTraverse(BinaryTreeNode root)
{
BinaryTreeNode T=root;
Stack s=new Stack();
Queue q=new LinkedList();
s.push(root);
while(!s.isEmpty())
{
T=s.pop();
q.push(T);
if(T.rightChild!=null)
s.push(T.rightChild);
if(T.leftChild!=null)
s.push(T.leftChild);
}
//用於得到先序遍歷的結果
while(!q.isEmpty())
{
System.out.println(((BinaryTreeNode)q.pop()).data);
}
}第二種:
藉助一個棧來記載當前被訪問節點的右孩子節點,以便在遍歷完一個節點的左子樹後,能夠順利的進入這個節點的右子樹進行遍歷。從二叉樹的根節點出發,沿著該節點的左子樹向下搜索,在搜索過程中遇到一個節點就先訪問該節點,並將該節點的非空右孩子節點壓入棧中,當左子樹訪問完成之後,從棧頂彈出一個節點的右孩子節點,然後用上述同樣的方法去遍歷該節點的右子樹,以此類推,直至二叉樹中的所有節點都被訪問了為止。其過程描述如下:
- 創建一個棧對象,根節點入棧
- 當棧為非空時,將棧頂節點彈出棧內並訪問該節點
- 對當前訪問節點的非空左孩子節點相繼依次訪問,並將當前訪問節點的非空右孩子節點壓入棧內
- 重覆執行步驟2和3,直到棧為空為止
示例代碼如下:
package queueandstack;
import java.util.Stack;
/**
* 用於演示二叉樹的遍歷的三種方式的代碼
* @author 學徒
*
*/
public class AroundTree
{
/**
* 用於實現二叉樹的非遞歸方式的先序遍歷,方式2
* @param root 二叉樹的根節點
*/
public void PreRootTraverse(BinaryTreeNode root)
{
BinaryTreeNode T=root;
if(T!=null)
{
Stack s=new Stack();
s.push(T);//根節點入棧
while(!s.isEmpty())
{
T=(BinaryTreeNode)s.pop();//移除棧頂節點,並返回其值
System.out.println(T.data);//訪問節點
while(T!=null)
{
if(T.leftChild!=null)//訪問左孩子節點
System.out.println(T.leftChild.data);//訪問節點
if(T.rightChild!=null)//右孩子非空入棧
s.push(T.rightChild);
T=T.leftChild;
}
}
}
}
}
中序遍歷:
所謂的中序遍歷是指對一棵二叉樹按照左子樹,根節點,右子樹的順序遞歸的在一棵二叉樹的左右子樹中訪問相關節點的方式。如圖1.1所示的一棵二叉樹,其中序遍歷的結果為DBEAC。
進行中序遍歷可以藉助一個棧來記載遍歷過程中所經歷的而未被訪問過的所有節點,以便遍歷完一個節點左子樹後能順利返回到它的父節點。實現中根遍歷操作的非遞歸演算法的主要思想是:從二叉樹的根節點出發,沿著該節點的左子樹向下搜索,在搜索過程中將所遇到的每一個節點依次壓棧,直到二叉樹中最坐下的的節點壓棧為止,然後從棧中彈出棧頂節點並對其進行訪問,訪問完後再進入該節點的右子樹並用上述的同樣的方法去遍歷該節點的右子樹,以此類推,直到二叉樹中的所有節點都被訪問為止。
示例代碼如下:
package queueandstack;
import java.util.Stack;
/**
* 用於演示二叉樹的遍歷的三種方式的代碼
* @author 學徒
*
*/
public class AroundTree
{
/**
* 用於實現二叉樹的非遞歸方式的中序遍歷
* @param root 二叉樹的根節點
*/
public void PreRootTraverse(BinaryTreeNode root)
{
BinaryTreeNode T=root;
if(T!=null)
{
Stack s=new Stack();
s.push(T);
while(!s.isEmpty())
{
while(s.peek()!=null)//將棧頂節點的左孩子節點相繼入棧
s.push(((BinaryTreeNode)s.peek()).leftChild);
s.pop();//空節點退棧
//在遍歷節點時,將該節點對應的右孩子節點壓入棧中
if(!s.isEmpty())
{
T=(BinaryTreeNode)s.pop();//得到未訪問的棧頂節點,並返回其值
System.out.println(T.data);
s.push(T.rightChild);//節點的右孩子入棧
}
}
}
}
}


