昨天在QQ群上看到一道題,“求1-1000中能被3或5整除的數字之和” 其中看到很有趣的解法二,最開始還是挺迷惑的, 後來想了下,再經人指點,就覺得茅塞頓開。 第一種解法很普遍,就是將1000以內的數都遍歷一遍,只要有整除3或者整除5的數,就將其加起來,最終得到一個總的和。 讓我感興趣的是第二種解法
昨天在QQ群上看到一道題,“求1-1000中能被3或5整除的數字之和”
其中看到很有趣的解法二,最開始還是挺迷惑的, 後來想了下,再經人指點,就覺得茅塞頓開。

第一種解法很普遍,就是將1000以內的數都遍歷一遍,只要有整除3或者整除5的數,就將其加起來,最終得到一個總的和。
讓我感興趣的是第二種解法,這裡巧妙運用了數學上的等差數列
一個公差為 的等差數列
的等差數列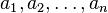 前
前 項的級數為:
項的級數為:
![S_n = a_1+a_2+\dots+a_n=\sum_{i=0}^{n-1} (a_1+id)=\frac{n( a_1 + a_n)}{2} =\frac{n[ 2a_1 + (n-1)d ]}{2}.](https://upload.wikimedia.org/math/2/0/a/20a19b4e5511d45a905b0405b44ddfc8.png)
- 第二種方法第一步就用了(a1+an)/3*3,所以就變成了3*(1+333)*333/2,這一步就是把整除3的所有項都加起來。
- 同理,sum(Math.floor(input-1)/5))*5中,就把1000以內中能整除5的所有項都加起來
- 最後能整除3和整除5裡面有重覆的數,比如15,這時就把重覆除以15的數減掉,就能獲得1000以內能被3或5整除的數字之和。



