演算法（第四版）C#題解——1.4

寫在前面整個項目都托管在了 Github 上：https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp這一節內容可能會用到的庫文件有 Measurement 和 TestCase，同樣在 Github 上可以找到。善用 Ctrl + F... ...

寫在前面

整個項目都托管在了 Github 上：https://github.com/ikesnowy/Algorithms-4th-Edition-in-Csharp

這一節內容可能會用到的庫文件有 Measurement 和 TestCase，同樣在 Github 上可以找到。

善用 Ctrl + F 查找題目。

習題&題解

1.4.1

題目

證明從 N 個數中取三個整數的不同組合總數為 N(N - 1)(N - 2) / 6。

解答

即為證明組合計算公式：

C(N, 3)

= N! / [(N - 3)! × 3!]
= [(N - 2) * (N - 1) * N] / 3!
= N(N - 1)(N - 2) / 6

顯然 N 必須大於等於 3。
N = 3 時公式正確，只有一種組合。
N = 4 時公式正確，只有四種組合。

擴展到 N+1 個數，將 N = N + 1 代入，可得：
(N + 1)N(N - 1) / 6
N + 1 個數能組成的三位數組合可以這樣理解
前 N 個數中取三個數的所有組合 +多出的一個數和前 N 個數中的任意取兩個數的所有組合
即為 N(N-1)(N - 2) / 6 + C(N, 2)
變形後即為(N + 1)N(N - 1) / 6

得證。

1.4.2

題目

修改 ThreeSum，正確處理兩個較大 int 值相加可能溢出的情況。

解答

將 a[i] + a[j] + a[k] 改為 (long)a[i] + a[j] + a[k] 即可。

此時整個式子將按照精度最高（也就是 long）的標準計算。

long.MaxValue = 9223372036854775807 > int.MaxValue * 3 = 6442450941

代碼

namespace Measurement
{
    /// <summary>
    /// 用暴力方法尋找數組中和為零的三元組。
    /// </summary>
    public static class ThreeSum
    {
        /// <summary>
        /// 輸出所有和為零的三元組。
        /// </summary>
        /// <param name="a">輸入數組。</param>
        public static void PrintAll(int[] a)
        {
            int n = a.Length;
            for (int i = 0; i < n; ++i)
            {
                for (int j = i + 1; j < n; ++j)
                {
                    for (int k = j + 1; k < n; ++k)
                    {
                        if ((long)a[i] + a[j] + a[k] == 0)
                        {
                            Console.WriteLine($"{a[i]} + {a[j]} + {a[k]}");
                        }
                    }
                }
            }
        }

        /// <summary>
        /// 計算和為零的三元組的數量。
        /// </summary>
        /// <param name="a">輸入數組。</param>
        /// <returns></returns>
        public static int Count(int[] a)
        {
            int n = a.Length;
            int count = 0;
            for (int i = 0; i < n; ++i)
            {
                for (int j = i + 1; j < n; ++j)
                {
                    for (int k = j + 1; k < n; ++k)
                    {
                        if ((long)a[i] + a[j] + a[k] == 0)
                        {
                            count++;
                        }
                    }
                }
            }
            return count;
        }
    }
}

1.4.3

題目

修改 DoublingTest，使用 StdDraw 產生類似於正文中的標準圖像和對數圖像，
根據需要調整比例使圖像總能夠充滿視窗的大部分區域。

解答

見代碼，這裡貼出繪圖函數，窗體只是在得到測試結果之後簡單調用以下這兩個函數。

代碼

public static void PaintLinear(double[] testResult)
        {
            //新建一個繪圖視窗
            Form2 linear = new Form2();
            linear.Show();
            //新建畫布
            Graphics canvas = linear.CreateGraphics();
            //獲取視窗區域
            Rectangle rect = linear.ClientRectangle;
            //計算單位長度（十等分）
            int unitY = rect.Height / 10;
            int unitX = rect.Width / 10;
            //獲取中心區域（上下左右增加 10% 的內補）
            Rectangle center = new Rectangle(rect.X + unitX, rect.Y + unitY, unitX * 8, unitY * 8);
            //繪製坐標系
            canvas.DrawLine(Pens.Black, center.X, center.Y, center.X, center.Y + center.Height);
            canvas.DrawLine(Pens.Black, center.X, center.Y + center.Height, center.X + center.Width, center.Y + center.Height);
            //對 X 軸 10 等分，對 Y 軸 10 等分
            int xaxisUnit = center.Width / 10;
            int yaxisUnit = center.Height / 10;
            //標記 X 軸坐標值
            for (int i = 1; i <= 8; i += i)
            {
                canvas.DrawString(i + "N", linear.Font, Brushes.Black, center.X + i * xaxisUnit, center.Y + center.Height);
            }
            //反轉坐標系
            canvas.TranslateTransform(0, linear.ClientRectangle.Height);
            canvas.ScaleTransform(1, -1);
            //計算單位長度
            double Unit = center.Height / testResult[3];
            //標記
            PointF[] result = new PointF[4];
            for (int i = 0, j = 1; i < 4 && j <= 8; ++i, j += j)
            {
                result[i] = new PointF(center.X + j * xaxisUnit, (float)(center.Y + Unit * testResult[i]));
            }
            //鏈接
            canvas.DrawLines(Pens.Black, result);

            canvas.Dispose();
        }

        public static void PaintLogarithm(double[] testResult)
        {
            //新建一個繪圖視窗
            Form2 log = new Form2();
            log.Show();
            //新建畫布
            Graphics canvas = log.CreateGraphics();
            //獲取視窗區域
            Rectangle rect = log.ClientRectangle;
            //計算單位長度（十等分）
            int unitY = rect.Height / 10;
            int unitX = rect.Width / 10;
            //獲取中心區域（上下左右增加 10% 的內補）
            Rectangle center = new Rectangle(rect.X + unitX, rect.Y + unitY, unitX * 8, unitY * 8);
            //繪製坐標系
            canvas.DrawLine(Pens.Black, center.X, center.Y, center.X, center.Y + center.Height);
            canvas.DrawLine(Pens.Black, center.X, center.Y + center.Height, center.X + center.Width, center.Y + center.Height);
            //對 X 軸 10 等分，對 Y 軸 10 等分
            int xaxisUnit = center.Width / 10;
            int yaxisUnit = center.Height / 10;
            //標記 X 軸坐標值
            for (int i = 1; i <= 8; i += i)
            {
                canvas.DrawString(i + "N", log.Font, Brushes.Black, center.X + i * xaxisUnit, center.Y + center.Height);
            }
            //反轉坐標系
            canvas.TranslateTransform(0, log.ClientRectangle.Height);
            canvas.ScaleTransform(1, -1);
            //計算單位長度
            double Unit = center.Height / testResult[3];
            //標記
            PointF[] result = new PointF[4];
            for (int i = 0, j = 1; i < 4 && j <= 8; ++i, j += j)
            {
                result[i] = new PointF(center.X + j * xaxisUnit, (float)(center.Y + Unit * testResult[i]));
            }
            //鏈接
            canvas.DrawLines(Pens.Black, result);
            canvas.Dispose();
        }

1.4.4

題目

參照表 1.4.4 為 TwoSum 建立一張類似的表格。

解答

代碼分塊↑

時間分析↓

1.4.5

題目

給出下麵這些量的近似：
a. N + 1
b. 1 + 1/N
c. (1 + 1/N)(1 + 2/N)
d. 2N^3 - 15N^2 + N
e. lg(2N) / lgN
f. lg(N^2 + 1) / lgN
g. N^100 / 2^N

解答

類似於取極限的做法。

a. N

b. 1

c. 1

d. 2N³

e. 1

f. 2

g. N¹⁰⁰

1.4.6

題目

給出以下代碼段的運行時間的增長數量級（作為 N 的函數）。

int sum = 0;
for (int n = N; n > 0; n /= 2)
    for (int i = 0; i < n; i++)
        sum++;

int sum = 0;
for (int i = 1; i < N; i *= 2)
    for (int j = 0; j < i; j++)
        sum++;

int sum = 0;
for (int i = 1; i < N; i *= 2)
    for (int j = 0; j < N; j++)
        sum++;

解答

a. N + N/2 + N/4 + … = ~2N，線性。

b. 1 + 2 + 4 + … = ~2N，線性。

c. logN * N，線性對數。

1.4.7

題目

以統計涉及輸入數字的算數操作（和比較）的成本模型分析 ThreeSum。

解答

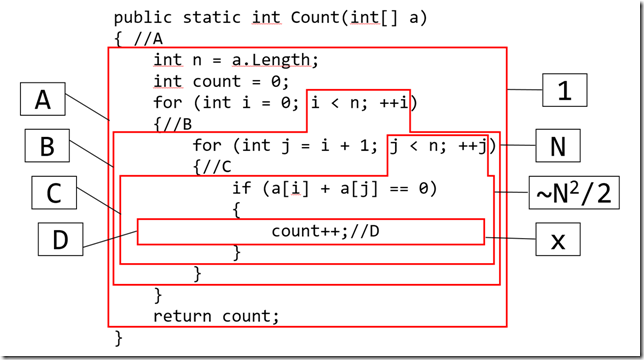
最外層迴圈進行了 N 次比較。

次外層迴圈進行了 N^2 次比較。

最裡層迴圈進行了 N^3 次比較。

內部 if 語句進行了 N^3 次比較。

if 內部進行了 N(N-1) 次加法。

加起來，~2N^3。

1.4.8

題目

編寫一個程式，計算輸入文件中相等的整數對的數量。
如果你的第一個程式是平方級別的，
請繼續思考並用 Array.sort() 給出一個線性對數級別的解答。

解答

平方級別：直接二層迴圈遍歷一遍。

線性對數：只遍歷一遍數組，在遍歷過程中用二分查找確認在剩餘數組中是否有相等的整數。

代碼

/// <summary>
        /// 暴力查找數組中相等的整數對。
        /// </summary>
        /// <param name="a">需要查找的數組。</param>
        /// <returns></returns>
        static int CountEqual(int[] a)
        {
            int n = a.Length;
            int count = 0;
            for (int i = 0; i < n; ++i)
            {
                for (int j = i + 1; j < n; ++j)
                {
                    if (a[i] == a[j])
                        count++;
                }
            }

            return count;
        }

暴力演算法↑

二分查找演算法↓

/// <summary>
        /// 利用二分查找進行優化的查找相等整數對演算法。
        /// </summary>
        /// <param name="a">需要查找的數組。</param>
        /// <returns></returns>
        static int CountEqualLog(int[] a)
        {
            int n = a.Length;
            int count = 0;
            Array.Sort(a);
            for (int i = 0; i < n; ++i)
            {
                if (BinarySearch.Rank(a[i], a, i + 1, a.Length - 1) != -1)
                {
                    count++;
                }
            }
            return count;
        }

1.4.9

題目

已知由倍率實驗可得某個程式的時間倍率為 2^b 且問題規模為 N0 時程式運行時間為 T，
給出一個公式預測該程式在處理規模為 N 的問題時所需的運行時間。

解答

1.4.10

題目

修改二分查找演算法，使之總是返回和被查找的鍵匹配的索引最小的元素。
（但仍能夠保證對數級別的運行時間）

解答

修改二分查找的結束條件，找到後仍然向左側尋找，如果還能找到更小的，則返回較小的下標；否則返回當前下標。

代碼

namespace _1._4._10
{
    /// <summary>
    /// 二分查找。
    /// </summary>
    public class BinarySearch
    {
        /// <summary>
        /// 用遞歸方法進行二分查找。
        /// </summary>
        /// <param name="key">關鍵字。</param>
        /// <param name="a">查找範圍。</param>
        /// <param name="lo">查找的起始下標。</param>
        /// <param name="hi">查找的結束下標。</param>
        /// <returns>返回下標，如果沒有找到則返回 -1。</returns>
        public static int Rank(int key, int[] a, int lo, int hi)
        {
            if (hi < lo)
                return -1;
            int mid = (hi - lo) / 2 + lo;
            if (a[mid] == key)
            {
                int mini = Rank(key, a, lo, mid - 1);
                if (mini != -1)
                    return mini;
                return mid;
            }
            else if (a[mid] < key)
            {
                return Rank(key, a, mid + 1, hi);
            }
            else
            {
                return Rank(key, a, lo, mid - 1);
            }
        }
    }
}

1.4.11

題目

為 StaticSETofInts （請見表 1.2.15）添加一個實例方法 howMany()，
找出給定鍵的出現次數且在最壞情況下所需的運行時間應該和 log(N) 成正比。

解答

這裡給出官網上的 Java 實現：StaticSETofInts.java。

howMany() 可以用二分查找實現，在找到一個值後繼續向兩側查找，最後返回找到的次數。

代碼

using System;

namespace Measurement
{
    /// <summary>
    /// 有序數組，能夠快速查找並自動維護其中的順序。
    /// </summary>
    public class StaticSETofInts
    {
        private int[] a;

        /// <summary>
        /// 用一個數組初始化有序數組。
        /// </summary>
        /// <param name="keys">源數組。</param>
        public StaticSETofInts(int[] keys)
        {
            this.a = new int[keys.Length];
            for (int i = 0; i < keys.Length; ++i)
            {
                this.a[i] = keys[i];
            }
            Array.Sort(this.a);
        }

        /// <summary>
        /// 檢查數組中是否存在指定元素。
        /// </summary>
        /// <param name="key">要查找的值。</param>
        /// <returns>存在則返回 true，否則返回 false。</returns>
        public bool Contains(int key)
        {
            return Rank(key, 0, this.a.Length - 1) != -1;
        }

        /// <summary>
        /// 返回某個元素在數組中存在的數量。
        /// </summary>
        /// <param name="key">關鍵值。</param>
        /// <returns>返回某個元素在數組中存在的數量。</returns>
        public int HowMany(int key)
        {
            int hi = this.a.Length - 1;
            int lo = 0;
            
            return HowMany(key, lo, hi);
        }

        /// <summary>
        /// 返回某個元素在數組中存在的數量。
        /// </summary>
        /// <param name="key">關鍵值。</param>
        /// <param name="lo">查找起始下標。</param>
        /// <param name="hi">查找結束下標。</param>
        /// <returns>返回某個元素在數組中存在的數量。</returns>
        private int HowMany(int key, int lo, int hi)
        {
            int mid = Rank(key, lo, hi);
            if (mid == -1)
                return 0;
            else
            {
                return 1 + HowMany(key, lo, mid - 1) + HowMany(key, mid + 1, hi);
            }
        }

        /// <summary>
        /// 二分查找。
        /// </summary>
        /// <param name="key">關鍵值。</param>
        /// <param name="lo">查找的起始下標。</param>
        /// <param name="hi">查找的結束下標。</param>
        /// <returns>返回關鍵值的下標，如果不存在則返回 -1。</returns>
        public int Rank(int key, int lo, int hi)
        {
            while (lo <= hi)
            {
                int mid = (hi - lo) / 2 + lo;
                if (key < this.a[mid])
                    hi = mid - 1;
                else if (key > this.a[mid])
                    lo = mid + 1;
                else
                    return mid;
            }
            return -1;
        }
    }
}

1.4.12

題目

編寫一個程式，有序列印給定的兩個有序數組（含有 N 個 int 值）中的所有公共元素，
程式在最壞情況下所需的運行時間應該和 N 成正比。

解答

由於兩個數組都是有序的，可以同時進行比較。

設 i, j 分別為兩個數組的下標。
如果 a[i] == a[j]，i 和 j 都向後移動一位。
如果 a[i] != a[j]，比較小的那個向後移動一位。
迴圈直到某個數組遍歷完畢。

這樣最後的時間複雜度 ~2N

代碼

using System;

namespace _1._4._12
{
    /*
     * 1.4.12
     * 
     * 編寫一個程式，有序列印給定的兩個有序數組（含有 N 個 int 值） 中的所有公共元素，
     * 程式在最壞情況下所需的運行時間應該和 N 成正比。
     * 
     */
    class Program
    {
        static void Main(string[] args)
        {
            int[] a = new int[4] { 2, 3, 4, 10 };
            int[] b = new int[6] { 1, 3, 3, 5, 10, 11 };

            //2N 次數組訪問，數組 a 和數組 b 各遍歷一遍
            for (int i = 0, j = 0; i < a.Length && j < b.Length; )
            {
                if (a[i] < b[j])
                {
                    i++;
                }
                else if (a[i] > b[j])
                {
                    j++;
                }
                else
                {
                    Console.WriteLine($"Common Element:{a[i]}, First index: (a[{i}], b[{j}])");
                    i++;
                    j++;
                }
            }

        }
    }
}

1.4.13

題目

根據正文中的假設分別給出表示以下數據類型的一個對象所需的記憶體量：
a. Accumulator
b. Transaction
c. FixedCapacityStackOfStrings，其容量為 C 且含有 N 個元素。
d. Point2D
e. Interval1D
f. Interval2D
g. Double

解答

對象的固定開銷用 Object 表示。

a. Accumulator

使用 1.2.4.3 節給出的實現。
= int * 1 + double + Object * 1

= 4 * 1 + 8 + 16 * 1 = 32

b. Transaction

= string * 1 + Date * 1 + double * 1 + Object * 1

= (40 + 16 + 4 + 4 + 2N) * 1 + (8 + 32) * 1 + 8 * 1 + 16 * 1

= 128 + 2N

c. FixedCapacityStackOfStrings

= string[] * 1 + string * N + int * 1 + Object * 1

= 24 * 1 + N * (64 + 2C) + 4 * 1 + 16 * 1

= N * (64 + 2C) + 44

= N * (64 + 2C) + 48（填充）

d.Point2D

= double * 2 + Object * 1

= 8 * 2 + 16 * 1

= 32

e.Interval1D

= double * 2 + Object * 1

= 8 * 2 + 16 * 1

= 32

f.Interval2D

= Interval1D * 2 + Object * 1

= (8 + 24) * 2 + 16 * 1

= 80

g.Double

= double * 1 + Object * 1

= 8 * 1 + 16 * 1

= 24

1.4.14

題目

4-sum。

為 4-sum 設計一個演算法。

解答

這裡給出暴力方法，將最內側迴圈換成二分查找即為優化版本。

代碼

using System;

namespace Measurement
{
    /// <summary>
    /// 用暴力方法查找數組中和為零的四元組。
    /// </summary>
    public static class FourSum
    {
        /// <summary>
        /// 輸出數組中所有和為 0 的四元組。
        /// </summary>
        /// <param name="a">包含所有元素的數組。</param>
        public static void PrintAll(long[] a)
        {
            int N = a.Length;
            for (int i = 0; i < N; ++i)
            {
                for (int j = i + 1; j < N; ++j)
                {
                    for (int k = j + 1; k < N; ++k)
                    {
                        for (int l = k + 1; l < N; ++l)
                        {
                            if (a[i] + a[j] + a[k] + a[l] == 0)
                            {
                                Console.WriteLine($"{a[i]} + {a[j]} + {a[k]} + {a[l]} = 0");
                            }
                        }
                    }
                }
            }
        }

        /// <summary>
        /// 計算和為零的四元組的數量。
        /// </summary>
        /// <param name="a">包含所有元素的數組。</param>
        /// <returns></returns>
        public static int Count(long[] a)
        {
            int N = a.Length;
            int cnt = 0;

            for (int i = 0; i < N; ++i)
            {
                for (int j = i + 1; j < N; ++j)
                {
                    for (int k = j + 1; k < N; ++k)
                    {
                        for (int l = k + 1; l < N; ++l)
                        {
                            if (a[i] + a[j] + a[k] + a[l] == 0)
                            {
                                cnt++;
                            }
                        }
                    }
                }
            }

            return cnt;
        }
    }
}

1.4.15

題目

快速 3-sum。
作為熱身，使用一個線性級別的演算法
（而非基於二分查找的線性對數級別的演算法）
實現 TwoSumFaster 來計算已排序的數組中和為 0 的整數對的數量。
用相同的思想為 3-sum 問題給出一個平方級別的演算法。

解答

由於數組已經排序（從小到大），負數在左側，正數在右側。
TwoSumFaster
設最左側下標為 lo，最右側下標為 hi。
如果 a[lo] + a[hi] > 0, 說明正數太大，hi--。
如果 a[lo] + a[hi] < 0，說明負數太小，lo++。
否則就找到了一對和為零的整數對，lo++, hi--。

ThreeSumFaster
對於數組中的每一個數 a，ThreeSum 問題就等於求剩餘數組中所有和為 -a 的 TwoSum 問題。
只要在 TwoSumFaster 外層再套一個迴圈即可。

代碼

/// <summary>
        /// TwoSum 的快速實現。（線性級別）
        /// </summary>
        /// <param name="a">需要查找的數組範圍。</param>
        /// <returns>數組中和為零的整數對數量。</returns>
        static int TwoSumFaster(int[] a)
        {
            int i = 0;
            int j = a.Length - 1;
            int count = 0;
            while (i != j)
            {
                if (a[i] + a[j] == 0)
                {
                    count++;
                    i++;
                    j--;
                }
                else if (a[i] + a[j] < 0)
                {
                    i++;
                }
                else
                {
                    j--;
                }
            }
            return count;
        }

        /// <summary>
        /// ThreeSum 的快速實現。（平方級別）
        /// </summary>
        /// <param name="a">需要查找的數組範圍。</param>
        /// <returns>數組中和為零的三元組數量。</returns>
        static int ThreeSumFaster(int[] a)
        {
            int count = 0;
            for (int i = 0; i < a.Length; ++i)
            {
                int lo = i + 1;
                int hi = a.Length - 1;
                while (lo <= hi)
                {
                    if (a[lo] + a[hi] + a[i] == 0)
                    {
                        count++;
                        lo++;
                        hi--;
                    }
                    else if (a[lo] + a[hi] + a[i] < 0)
                    {
                        lo++;
                    }
                    else
                    {
                        hi--;
                    }
                }
            }
            return count;
        }

1.4.16

題目

最接近一對（一維）。
編寫一個程式，給定一個含有 N 個 double 值的數組 a[]，
在其中找到一對最接近的值：兩者之差（絕對值）最小的兩個數。
程式在最壞情況下所需的運行時間應該是線性對數級別的。

解答

先將數組從小到大排序，再遍歷一遍即可得到差距最小的兩個數。

排序演算法需要消耗 NlogN，具體見 MSDN：Array.Sort 方法 (Array)。

代碼

using System;

namespace _1._4._16
{
    /*
     * 1.4.16
     * 
     * 最接近