[您有新的未分配科技點]可，可，可持久化！？------可持久化線段樹普及版講解

最近跑來打數據結構，於是我決定搞一發可持久化，然後發現……一發不可收啊…… 對於可持久化數據結構，其最大的特征是“歷史版本查詢”，即可以回到某一次修改之前的狀態，並繼續操作；而這種“歷史版本查詢”會衍生出其他一些強大的操作。今天，我們主要講解可持久化線段樹。其實，它的另外一個名字“主席樹”似乎更加 ...

最近跑來打數據結構，於是我決定搞一發可持久化，然後發現……一發不可收啊……

對於可持久化數據結構，其最大的特征是“歷史版本查詢”，即可以回到某一次修改之前的狀態，並繼續操作；而這種“歷史版本查詢”會衍生出其他一些強大的操作。

今天，我們主要講解可持久化線段樹。其實，它的另外一個名字“主席樹”似乎更加為人所知（主席%%%）。

主席樹與普通的線段樹相比，多出來的操作是在修改時複製修改的一條鏈，這個操作的過程大概長下麵這樣。

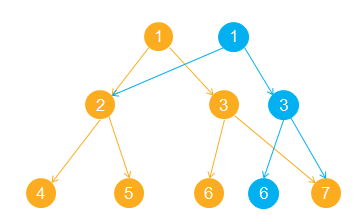
至於為什麼要這樣做……

對數據進行可持久化，一種朴素的想法是每一次修改新建一棵線段樹，但是，時間複雜度和空間複雜度都是不允許我們做這樣的操作的。

我們思考一下，每一次修改，只有一條鏈上的節點被修改，而其他的節點信息都沒有變。因此，我們對這一次修改新建包括一個新根在內的log_n個節點，其他的節點我們與上一課樹共用。這樣一來，我們既能保存之前的信息，又能進行修改操作。

主席樹插入操作代碼見下，有指針和數組2種版本：

指針版本：

 1 void insert(node *&a,node *b,int l,int r,int pos)
 2 {
 3     a->cnt=b->cnt+1;//cnt表示這一棵樹里的數據個數，a是新樹，b是舊樹，下同
 4     int mi=(l+r)>>1;
 5     if(l==r)return;
 6     if(pos<=mi)
 7     {
 8         a->ch[1]=b->ch[1],a->ch[0]=newnode();
 9         insert(a->ch[0],b->ch[0],l,mi,pos);
10     }
11     else 
12     {
13         a->ch[0]=b->ch[0],a->ch[1]=newnode();
14         insert(a->ch[1],b->ch[1],mi+1,r,pos);
15     }
16     a->update();
17 }

數組版本：

1 void insert(int rt1,int rt2,int l,int r,int pos)
2 {
3     if(l==r){cnt[rt1]=cnt[rt2]+1;return;}//cnt表示數據個數,rt1是新樹，rt2是舊樹
4     lc[rt1]=lc[rt2],rc[rt1]=rc[rt2];
5     int mi=(l+r)>>1;
6     if(pos<=mi)lc[rt1]=++tot,insert(lc[rt1],lc[rt2],l,mi,pos);
7     else rc[rt1]=++tot,insert(rc[rt1],rc[rt2],mi+1,r,pos);
8     cnt[rt1]=cnt[lc[rt1]]+cnt[rc[rt1]];
9 }

這一部分的基礎題大概有cogs2554（http://cogs.pro/cogs/problem/problem.php?pid=2554 ），這就是一道主席樹的入門水題，完全沒有瞭解的同學可以通過這道題來入門。

可能有同學註意到了上面插入代碼的cnt變數，它其實有大用：接下來，我們考慮用主席樹進行一些更高級的操作：維護靜態的區間第k大（小）值。

為什麼主席樹可以維護這個?

在對於一個序列查詢k大（小）值時，我們把主席樹建成權值線段樹，每插入一個數就新建一個版本。這時，不難看出主席樹具有區間可減性：

對於某一個區間【L,R】插入b個數以後區間中樹的個數，減去【L,R】插入a-1個數以後區間中數的個數，

結果就是區間【a，b】中權值在【L,R】的數的個數。這樣利用cnt變數不斷查詢，我們就可以找到某一個區間中第k大（小）的值

我們在代碼實現時，只需要同時傳入2個節點，並且比較區間數據個數之差與k的大小關係，進行移動即可

查詢操作代碼見下：

 1 inline int query(int l,int r,int u,int v,int k)
 2 {
 3     node *a=root[u-1],*b=root[v];
 4     while(l<r)
 5     {
 6         int tmp=b->ch[0]->cnt-a->ch[0]->cnt,mi=(l+r)>>1;
 7         if(tmp>=k)a=a->ch[0],b=b->ch[0],r=mi;
 8         else a=a->ch[1],b=b->ch[1],k-=tmp,l=mi+1;
 9     }
10     return r;
11 }

但是要註意，主席樹在不做額外處理時只能查詢靜態的區間k大（小）值。

接下來，我們就考慮動態區間k小值。如果我們要對區間進行修改的話，一個簡單的主席樹已經無法實現了。

如果對原來的節點直接修改的話，會造成不可名狀的運行錯誤（有興趣的同學可以結合上面插入代碼想一想為什麼），

空間和時間也無法接受（我們需要把後面所有樹都更改一下），但我們在做樹套樹的時候，可以做類似的操作，那麼主席樹是不是應該也套些什麼呢？

主席樹上的點，儲存的都是在一段權值區間內的數據個數，我們必須要維護數據個數才可以通過相減得到一段區間的權值線段樹。

而現在有了修改，對於這個修改的維護，朴素的做法有2種：O(1)查詢，O(n)維護（掃一遍），和O(n)查詢（現場算）和O(1)維護。

這兩種做法都不是很憂，所以我們考慮利用快捷維護首碼和的樹狀數組解決這個問題，即所謂“樹狀數組套主席樹”

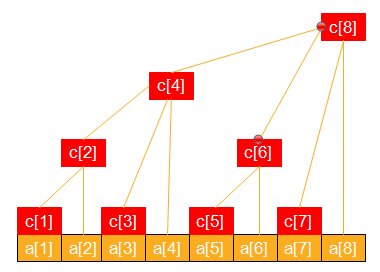
如圖，圖中c節點代表對應區間的線段樹。比如，第8個點代表的線段樹就是區間[1,8]的線段樹，而第6個點代表的就是區間[5,6]的線段樹。其他點同理。

在修改時，我們用樹狀數組找出需要修改的最多logn個節點，存起來，通過同時進行的一遍修改即可解決了。查詢是類似的。

普通的樹套樹題都可以用樹狀數組套主席樹來打，這裡給出幾道練習題：

bzoj3196 二逼平衡樹 http://www.lydsy.com/JudgeOnline/problem.php?id=3196

bzoj1901 Zju2112 Dynamic Rankings（許可權題）http://www.lydsy.com/JudgeOnline/problem.php?id=1901

cogs 257 動態排名系統 http://cogs.pro/cogs/problem/problem.php?pid=257

我cogs257 的代碼 http://www.cnblogs.com/LadyLex/p/7275540.html

上面這些還沒完。更強大的是，主席樹不僅可以進行數列的維護，還可以對樹上的數據進行操作和維護。

一般來說，我們有兩種方法實現主席樹上樹：

一種是在父親節點的基礎上，在兒子節點新建樹。這樣可以維護出從某個點到根節點之間的數組，從而與LCA衍生出求樹上某一條鏈的k值問題（或其他問題）

一種是按照兩個把樹轉化為序列的工具：dfs序和歐拉序來建樹，從而解決問題。這樣可以截出一棵子樹的值，從而衍生出其他問題。

為什麼第二種方法是正確的？如果我們按照左區間+1，右區間-1的話，如果某條路徑的另一端不在鏈上中，我們就不會統計到他的答案（+1的時間過於靠前或者靠後，導致沒有統計）這個東西的確很巧妙…… 這樣一來，如果查詢點，我們把待查詢的鏈拆成[x.lca]和[y.fa[lca]]然後查詢。如果我們統計的是邊，所以我們應該統計[x.lca]和[y.lca]。lca處的答案被統計了2次，最後記得減去；點的查詢大概長下麵這樣