Step1 Plotting the Data 在處理數據之前,我們通常要瞭解數據,對於這次的數據集合,我們可以通過離散的點來描繪它,在一個2D的平面里把它畫出來。 6.1101,17.592 5.5277,9.1302 8.5186,13.662 7.0032,11.854 5.8598,6.82 ...
Step1 Plotting the Data
在處理數據之前,我們通常要瞭解數據,對於這次的數據集合,我們可以通過離散的點來描繪它,在一個2D的平面里把它畫出來。

6.1101,17.592 5.5277,9.1302 8.5186,13.662 7.0032,11.854 5.8598,6.8233 8.3829,11.886 7.4764,4.3483 8.5781,12 6.4862,6.5987 5.0546,3.8166 5.7107,3.2522 14.164,15.505 5.734,3.1551 8.4084,7.2258 5.6407,0.71618 5.3794,3.5129 6.3654,5.3048 5.1301,0.56077 6.4296,3.6518 7.0708,5.3893 6.1891,3.1386 20.27,21.767 5.4901,4.263 6.3261,5.1875 5.5649,3.0825 18.945,22.638 12.828,13.501 10.957,7.0467 13.176,14.692 22.203,24.147 5.2524,-1.22 6.5894,5.9966 9.2482,12.134 5.8918,1.8495 8.2111,6.5426 7.9334,4.5623 8.0959,4.1164 5.6063,3.3928 12.836,10.117 6.3534,5.4974 5.4069,0.55657 6.8825,3.9115 11.708,5.3854 5.7737,2.4406 7.8247,6.7318 7.0931,1.0463 5.0702,5.1337 5.8014,1.844 11.7,8.0043 5.5416,1.0179 7.5402,6.7504 5.3077,1.8396 7.4239,4.2885 7.6031,4.9981 6.3328,1.4233 6.3589,-1.4211 6.2742,2.4756 5.6397,4.6042 9.3102,3.9624 9.4536,5.4141 8.8254,5.1694 5.1793,-0.74279 21.279,17.929 14.908,12.054 18.959,17.054 7.2182,4.8852 8.2951,5.7442 10.236,7.7754 5.4994,1.0173 20.341,20.992 10.136,6.6799 7.3345,4.0259 6.0062,1.2784 7.2259,3.3411 5.0269,-2.6807 6.5479,0.29678 7.5386,3.8845 5.0365,5.7014 10.274,6.7526 5.1077,2.0576 5.7292,0.47953 5.1884,0.20421 6.3557,0.67861 9.7687,7.5435 6.5159,5.3436 8.5172,4.2415 9.1802,6.7981 6.002,0.92695 5.5204,0.152 5.0594,2.8214 5.7077,1.8451 7.6366,4.2959 5.8707,7.2029 5.3054,1.9869 8.2934,0.14454 13.394,9.0551 5.4369,0.61705ex1data1.txt
我們把ex1data1中的內容讀取到X變數和y變數中,用m表示數據長度。
data = load('ex1data1.txt');
X = data(:,1);
y = data(:,2);
m = length(y);
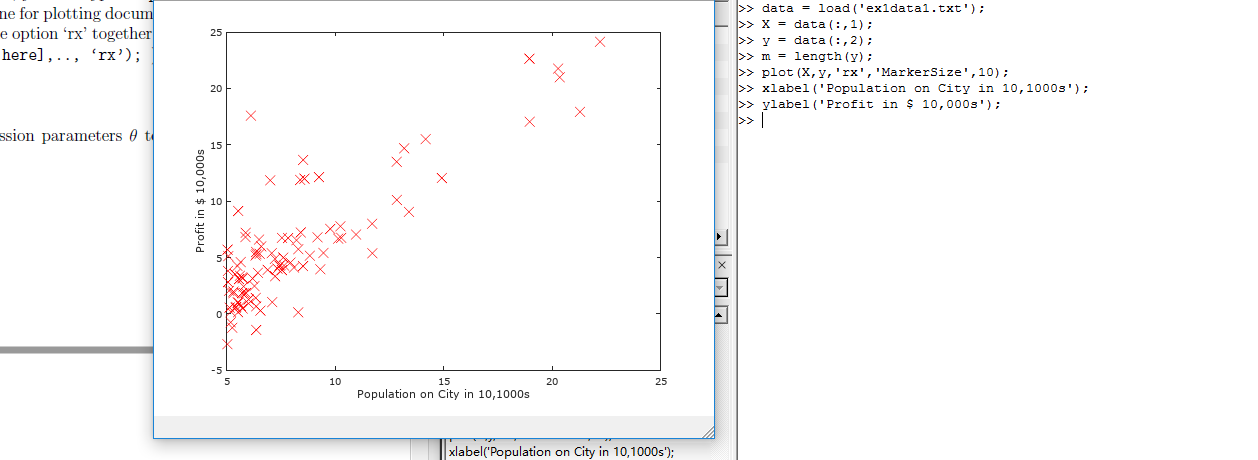
接下來通過圖像描繪出來。
plot(x,y,'rx','MakerSize',10);
ylabel('Profit in $10,000s');
xlabel('Population of City in 10,000s');
現在我們得到圖像如圖所示,就是原始的數據的直觀表示。
Step2 Gradient Descent
現在,我們通過梯度下降法對參數θ進行線性回歸。
依照我們之前所得出步驟方法

迭代更新
計算θ值函數:
function J = computeCost(X, y, theta) %COMPUTECOST Compute cost for linear regression % J = COMPUTECOST(X, y, theta) computes the cost of using theta as the % parameter for linear regression to fit the data points in X and y % Initialize some useful values m = length(y); % number of training examples % You need to return the following variables correctly J = 0; % ====================== YOUR CODE HERE ====================== % Instructions: Compute the cost of a particular choice of theta % You should set J to the cost. J = sum((X * theta - y).^2) / (2*m); % X(79,2) theta(2,1) % ========================================================================= end
接下來是梯度下降函數
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
theta_s=theta;
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
theta(1) = theta(1) - alpha / m * sum(X * theta_s - y);
theta(2) = theta(2) - alpha / m * sum((X * theta_s - y) .* X(:,2));
% 必須同時更新theta(1)和theta(2),所以不能用X * theta,而要用theta_s存儲上次結果。
theta_s=theta;
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
end
J_history
end
繪圖函數:
function plotData(x, y)
%PLOTDATA Plots the data points x and y into a new figure
% PLOTDATA(x,y) plots the data points and gives the figure axes labels of
% population and profit.
% ====================== YOUR CODE HERE ======================
% Instructions: Plot the training data into a figure using the
% "figure" and "plot" commands. Set the axes labels using
% the "xlabel" and "ylabel" commands. Assume the
% population and revenue data have been passed in
% as the x and y arguments of this function.
%
% Hint: You can use the 'rx' option with plot to have the markers
% appear as red crosses. Furthermore, you can make the
% markers larger by using plot(..., 'rx', 'MarkerSize', 10);
figure; % open a new figure window
plot(x, y, 'rx', 'MarkerSize', 10); % Plot the data
ylabel('Profit in $10,000s'); % Set the y axis label
xlabel('Population of City in 10,000s'); % Set the x axis label
% ============================================================
end
根據以上函數,我們進行線性回歸:
%% Machine Learning Online Class - Exercise 1: Linear Regression % Instructions % ------------ % % This file contains code that helps you get started on the % linear exercise. You will need to complete the following functions % in this exericse: % % warmUpExercise.m % plotData.m % gradientDescent.m % computeCost.m % gradientDescentMulti.m % computeCostMulti.m % featureNormalize.m % normalEqn.m % % For this exercise, you will not need to change any code in this file, % or any other files other than those mentioned above. % % x refers to the population size in 10,000s % y refers to the profit in $10,000s % %% ==================== Part 1: Basic Function ==================== % Complete warmUpExercise.m fprintf('Running warmUpExercise ... \n'); fprintf('5x5 Identity Matrix: \n'); warmUpExercise() fprintf('Program paused. Press enter to continue.\n'); pause; %% ======================= Part 2: Plotting ======================= fprintf('Plotting Data ...\n') data = load('ex1data1.txt'); X = data(:, 1); y = data(:, 2); m = length(y); % number of training examples % Plot Data % Note: You have to complete the code in plotData.m plotData(X, y); fprintf('Program paused. Press enter to continue.\n'); pause; %% =================== Part 3: Gradient descent =================== fprintf('Running Gradient Descent ...\n') X = [ones(m, 1), data(:,1)]; % Add a column of ones to x theta = zeros(2, 1); % initialize fitting parameters % Some gradient descent settings iterations = 1500; alpha = 0.01; % compute and display initial cost computeCost(X, y, theta) % run gradient descent theta = gradientDescent(X, y, theta, alpha, iterations); % print theta to screen fprintf('Theta found by gradient descent: '); fprintf('%f %f \n', theta(1), theta(2)); % Plot the linear fit hold on; % keep previous plot visible plot(X(:,2), X*theta, '-') legend('Training data', 'Linear regression') hold off % don't overlay any more plots on this figure % Predict values for population sizes of 35,000 and 70,000 predict1 = [1, 3.5] *theta; fprintf('For population = 35,000, we predict a profit of %f\n',... predict1*10000); predict2 = [1, 7] * theta; fprintf('For population = 70,000, we predict a profit of %f\n',... predict2*10000); fprintf('Program paused. Press enter to continue.\n'); pause; %% ============= Part 4: Visualizing J(theta_0, theta_1) ============= fprintf('Visualizing J(theta_0, theta_1) ...\n') % Grid over which we will calculate J theta0_vals = linspace(-10, 10, 100); theta1_vals = linspace(-1, 4, 100); % initialize J_vals to a matrix of 0's J_vals = zeros(length(theta0_vals), length(theta1_vals)); % Fill out J_vals for i = 1:length(theta0_vals) for j = 1:length(theta1_vals) t = [theta0_vals(i); theta1_vals(j)]; J_vals(i,j) = computeCost(X, y, t); end end % Because of the way meshgrids work in the surf command, we need to % transpose J_vals before calling surf, or else the axes will be flipped J_vals = J_vals'; % Surface plot figure; surf(theta0_vals, theta1_vals, J_vals) xlabel('\theta_0'); ylabel('\theta_1'); % Contour plot figure; % Plot J_vals as 15 contours spaced logarithmically between 0.01 and 100 contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20)) xlabel('\theta_0'); ylabel('\theta_1'); hold on; plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);

如圖所示,繪製出線性回歸函數。
這時所繪製2D等高線圖梯度下降錶面圖:
function [X_norm, mu, sigma] = featureNormalize(X)
%FEATURENORMALIZE Normalizes the features in X
% FEATURENORMALIZE(X) returns a normalized version of X where
% the mean value of each feature is 0 and the standard deviation
% is 1. This is often a good preprocessing step to do when
% working with learning algorithms.
% You need to set these values correctly
X_norm = X;
mu = zeros(1, size(X, 2)); % mean value 均值 size(X,2) 列數
sigma = zeros(1, size(X, 2)); % standard deviation 標準差
% ====================== YOUR CODE HERE ======================
% Instructions: First, for each feature dimension, compute the mean
% of the feature and subtract it from the dataset,
% storing the mean value in mu. Next, compute the
% standard deviation of each feature and divide
% each feature by it's standard deviation, storing
% the standard deviation in sigma.
%
% Note that X is a matrix where each column is a
% feature and each row is an example. You need
% to perform the normalization separately for
% each feature.
%
% Hint: You might find the 'mean' and 'std' functions useful.
%
mu = mean(X); % mean value
sigma = std(X); % standard deviation
X_norm = (X - repmat(mu,size(X,1),1)) ./ repmat(sigma,size(X,1),1);
% ============================================================
end
function [theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters)
%GRADIENTDESCENTMULTI Performs gradient descent to learn theta
% theta = GRADIENTDESCENTMULTI(x, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCostMulti) and gradient here.
%
theta = theta - alpha / m * X' * (X * theta - y);
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCostMulti(X, y, theta);
end
end
function J = computeCostMulti(X, y, theta)
%COMPUTECOSTMULTI Compute cost for linear regression with multiple variables
% J = COMPUTECOSTMULTI(X, y, theta) computes the cost of using theta as the
% parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
% You should set J to the cost.
J = sum((X * theta - y).^2) / (2*m);
% =========================================================================
end
function [theta] = normalEqn(X, y)
%NORMALEQN Computes the closed-form solution to linear regression
% NORMALEQN(X,y) computes the closed-form solution to linear
% regression using the normal equations.
theta = zeros(size(X, 2), 1);
% ====================== YOUR CODE HERE ======================
% Instructions: Complete the code to compute the closed form solution
% to linear regression and put the result in theta.
%
% ---------------------- Sample Solution ----------------------
theta = pinv( X' * X ) * X' * y;
% -------------------------------------------------------------
% ============================================================
end
%% Machine Learning Online Class
% Exercise 1: Linear regression with multiple variables
%
% Instructions
% ------------
%
% This file contains code that helps you get started on the
% linear regression exercise.
%
% You will need to complete the following functions in this
% exericse:
%
% warmUpExercise.m
% plotData.m
% gradientDescent.m
% computeCost.m
% gradientDescentMulti.m
% computeCostMulti.m
% featureNormalize.m
% normalEqn.m
%
% For this part of the exercise, you will need to change some
% parts of the code below for various experiments (e.g., changing
% learning rates).
%
%% Initialization
%% ================ Part 1: Feature Normalization ================
%% Clear and Close Figures
clear ; close all; clc
fprintf('Loading data ...\n');
%% Load Data
data = load('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Print out some data points
fprintf('First 10 examples from the dataset: \n');
fprintf(' x = [%.0f %.0f], y = %.0f \n', [X(1:10,:) y(1:10,:)]');
fprintf('Program paused. Press enter to continue.\n');
pause;
% Scale features and set them to zero mean
fprintf('Normalizing Features ...\n');
[X mu sigma] = featureNormalize(X); % 均值0,標準差1
% Add intercept term to X
X = [ones(m, 1) X];
%% ================ Part 2: Gradient Descent ================
% ====================== YOUR CODE HERE ======================
% Instructions: We have provided you with the following starter
% code that runs gradient descent with a particular
% learning rate (alpha).
%
% Your task is to first make sure that your functions -
% computeCost and gradientDescent already work with
% this starter code and support multiple variables.
%
% After that, try running gradient descent with
% different values of alpha and see which one gives
% you the best result.
%
% Finally, you should complete the code at the end
% to predict the price of a 1650 sq-ft, 3 br house.
%
% Hint: By using the 'hold on' command, you can plot multiple
% graphs on the same figure.
%
% Hint: At prediction, make sure you do the same feature normalization.
%
fprintf('Running gradient descent ...\n');
% Choose some alpha value
alpha = 0.01;
num_iters = 8500;
% Init Theta and Run Gradient Descent
theta = zeros(3, 1);
[theta, J_history] = gradientDescentMulti(X, y, theta, alpha, num_iters);
% Plot the convergence graph
figure;
plot(1:numel(J_history), J_history, '-b', 'LineWidth', 2);
xlabel('Number of iterations');
ylabel('Cost J');
% Display gradient descent's result
fprintf('Theta computed from gradient descent: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
% Recall that the first column of X is all-ones. Thus, it does
% not need to be normalized.
price = [1 (([1650 3]-mu) ./ sigma)] * theta ;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using gradient descent):\n $%f\n'], price);
fprintf('Program paused. Press enter to continue.\n');
pause;
%% ================ Part 3: Normal Equations ================
fprintf('Solving with normal equations...\n');
% ====================== YOUR CODE HERE ======================
% Instructions: The following code computes the closed form
% solution for linear regression using the normal
% equations. You should complete the code in
% normalEqn.m
%
% After doing so, you should complete this code
% to predict the price of a 1650 sq-ft, 3 br house.
%
%% Load Data
data = csvread('ex1data2.txt');
X = data(:, 1:2);
y = data(:, 3);
m = length(y);
% Add intercept term to X
X = [ones(m, 1) X];
% Calculate the parameters from the normal equation
theta = normalEqn(X, y);
% Display normal equation's result
fprintf('Theta computed from the normal equations: \n');
fprintf(' %f \n', theta);
fprintf('\n');
% Estimate the price of a 1650 sq-ft, 3 br house
% ====================== YOUR CODE HERE ======================
price = [1 1650 3] * theta ;
% ============================================================
fprintf(['Predicted price of a 1650 sq-ft, 3 br house ' ...
'(using normal equations):\n $%f\n'], price);
處理前:
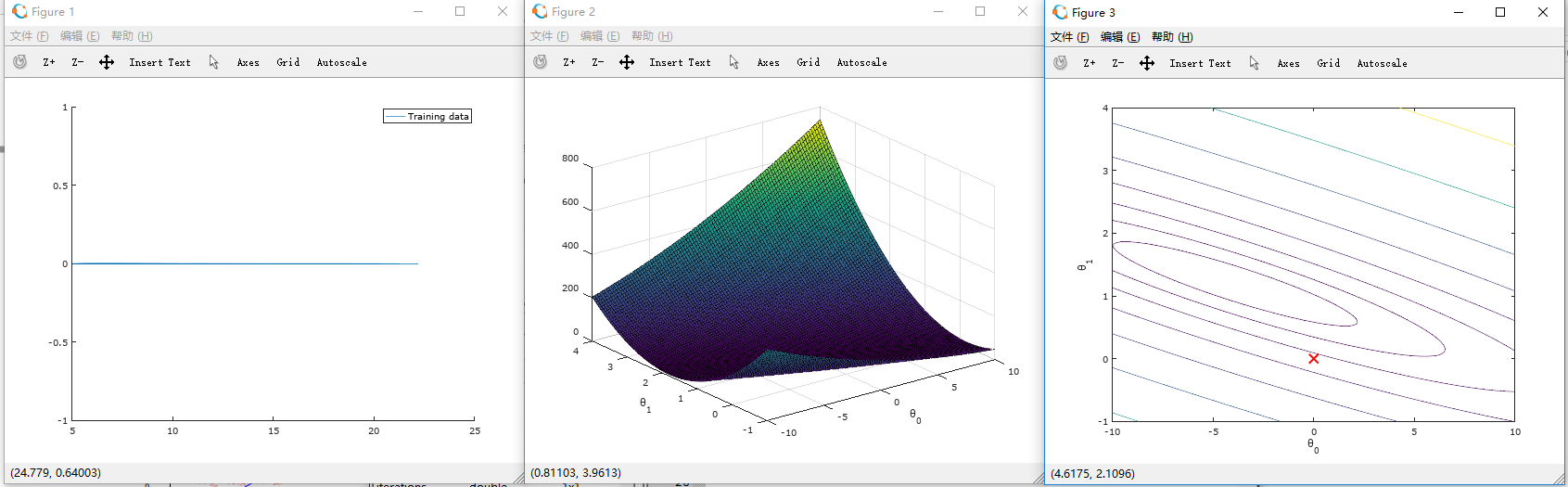
處理後:
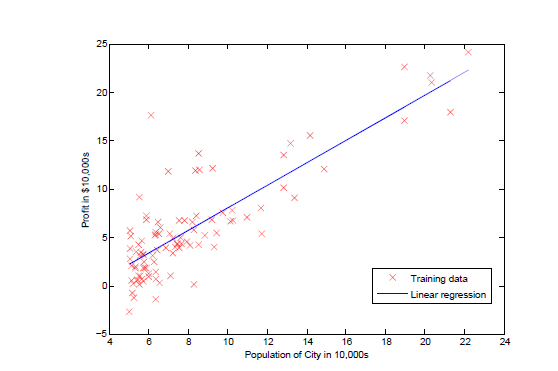
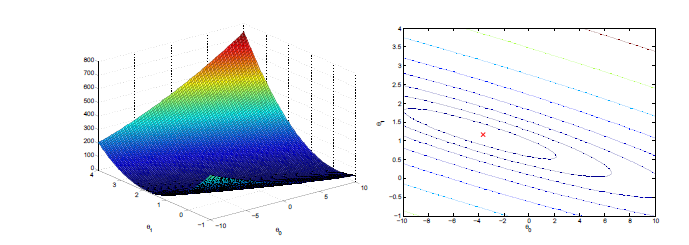
回歸過程如圖所示:
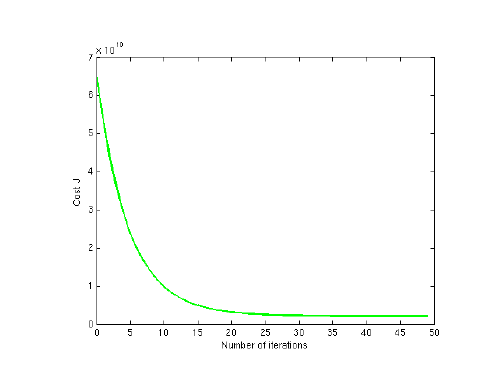
至此,我們通過梯度下降法解決了此問題,我們還可以通過之前所說的數學方法來解決,但是對於數據太大的情況(通常大於10000),我們就會通過梯度下降法來解決了
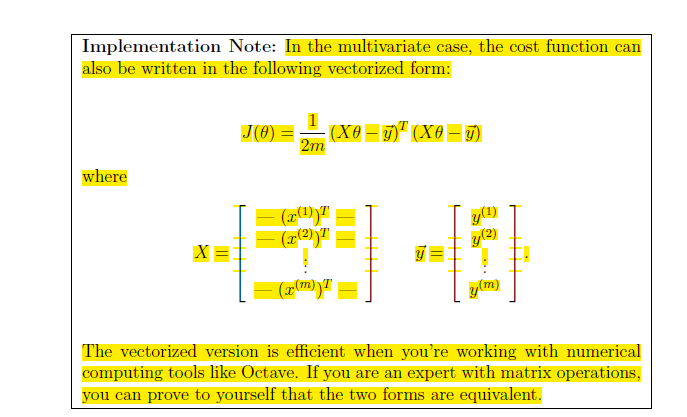
根據以上函數,我們進行線性回歸:




