3.比較排序之堆排序

　　對於堆排序會涉及一些完全二叉樹知識。對於待排序列{10, 2, 11, 8, 7}，把它看成是一顆完全二叉樹，如下圖所示。

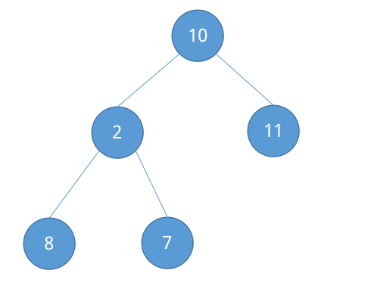
　　堆分為大根堆和小根堆：大根堆表示每個根節點均大於其子節點（L(i) >= L(2i) && L(i) >= L(2i + 1)），小根堆表示每個根節點均小於其子節點（L(i) <= L(2i) && L(i) <= L(2i + 1)）。（在完全二叉樹中第i個節點的左子節點為2i，其右位元組點為2i + 1）

　　本文將以大根堆的構建作為示例進行講解。

　　堆排序的第一步——構建初始堆。如何構建初始堆呢？根據定義，關鍵點在於每個根節點。觀察上述待排序列的完全二叉樹，不難發現存在節點2和節點10有子節點，它們是需要關註的節點。

　　如何定位節點2呢？發現它是葉子節點，或者最後一個節點的父節點，根據完全二叉樹的性質可知，除根節點外任意節點的父節點的編號為⌊n / 2⌋。已知n = 5，易知節點2的編號為⌊5 / 2⌋ = ②。比較它與左右子節點的大小並調整。

　　最後剩下根節點10，已知節點2的編號為②，② - 1 = ①即得到根節點10的編號。比較它與左右子節點的大小並調整。

　　調整完畢後發現已經構成了一個“大根堆”，示例中的待排序列較為簡單，再給出一個較為複雜的待排序列，觀察其構建大根堆的過程。對於待排序列{53, 17, 78, 09, 45, 65, 87, 32}，將它看成一顆完全二叉樹。

　　同樣我們來看它所需要關註的節點有哪些。

　　根據第一個例子，我們很容易能定位節點09的編號為⌊8 / 2⌋ = ④，節點78的編號為④ - 1 = ③……，依次類推，發現了一定的規律，即需要調整的節點位置從⌊n / 2⌋開始依次遞減直到根節點①結束(⌊n / 2⌋ ~ 1)。現在開始調整。

　　在第四次調整結束後發現節點53不滿足大根堆的定義，其右子節點大於它，此時需要做進一步的向下調整。

　　註意向下調整是每次向上調整的時候都需要做的判斷是否需要向下調整，而不是在所有的向上調整結束過後再回過頭來向下調整。這樣大根堆就建立好了，此時待排序列數組情況已經發生了改變：{87, 45, 78, 32, 17, 65, 53, 09}。接下來是如何進行排序的問題。將大根堆的根節點與最後一個節點互換，並調整二叉樹使其仍然滿足大根堆。

　　可以看到將根節點與最後一個節點呼喚後，待排序列的最大值已經放到了數組的最後一個位置{……, 87}，此時完成了第一趟排序，但這第一趟排序還沒有結束，此時除節點87外，其餘節點並不滿足大根堆的條件，所以需要對其餘節點進行調整為大根堆。排序過程不再給出，Java和Python3的代碼實現如下。

　　Java

 1 package com.algorithm.sort.heap;
 2 
 3 import java.util.Arrays;
 4 
 5 /**
 6  * 堆排序
 7  * Created by yulinfeng on 6/20/17.
 8  */
 9 public class Heap {
10     
11     public static void main(String[] args) {
12         int[] nums = {53, 17, 78, 09, 45, 65, 87, 32};
13         nums = heapSort(nums);
14         System.out.println(Arrays.toString(nums));
15     }
16     
17     /**
18      * 堆排序
19      * @param nums 待排序數組序列
20      * @return 排好序的數組序列
21      */
22     private static int[] heapSort(int[] nums) {
23     
24         for (int i = nums.length / 2 - 1; i >= 0; i--) {
25             heapAdjust(nums, i, nums.length);
26         }
27         for (int i = nums.length - 1; i > 0; i--) {
28             int temp = nums[i];
29             nums[i] = nums[0];
30             nums[0] = temp;
31             heapAdjust(nums, 0, i);
32         }
33         return nums;
34     }
35     
36     /**
37      * 調整堆
38      *
39      * @param nums   待排序序列
40      * @param parent      待調整根節點
41      * @param length 數組序列長度
42      */
43     private static void heapAdjust(int[] nums, int parent, int length) {
44         int temp = nums[parent];
45         int childIndex = 2 * parent + 1;    //完全二叉樹節點i從編號1開始的左子節點位置在2i，此處數組下標從0開始，即左子節點所在數組索引位置為：2i + 1
46         while (childIndex  < length) {
47             if (childIndex + 1 < length && nums[childIndex] < nums[childIndex + 1]) {
48                 childIndex++;   //節點有右子節點，且右子節點大於左子節點，則選取右子節點
49             }
50             if (temp > nums[childIndex]) {
51                 break;  //如果選中節點大於其子節點，直接返回
52             }
53             nums[parent] = nums[childIndex];
54             parent = childIndex;
55             childIndex = 2 * parent + 1;    //繼續向下調整
56         }
57         nums[parent] = temp;
58     }
59 }

　　Python3

 1 #堆排序
 2 def heap_sort(nums):
 3 
 4     for i in range(int(len(nums) / 2 - 1), -1, -1):
 5         heap_adjust(nums, i, len(nums))
 6     
 7     for i in range(len(nums) - 1, -1, -1):
 8         temp = nums[i]
 9         nums[i] = nums[0]
10         nums[0] = temp
11         heap_adjust(nums, 0, i)
12     
13     return nums
14 
15 #調整堆
16 def heap_adjust(nums, parent, length):
17     
18     temp = nums[parent]
19     childIndex = 2 * parent + 1
20     while childIndex < length:
21         if childIndex + 1 < length and nums[childIndex] < nums[childIndex + 1]:
22             childIndex += 1
23         if temp > nums[childIndex]:
24             break
25         nums[parent] = nums[childIndex]
26         parent = childIndex
27         childIndex = 2 * parent + 1
28     
29     nums[parent] = temp
30         
31 nums = [53, 17, 78, 09, 45, 65, 87, 32]
32 nums = heap_sort(nums)
33 print(nums)