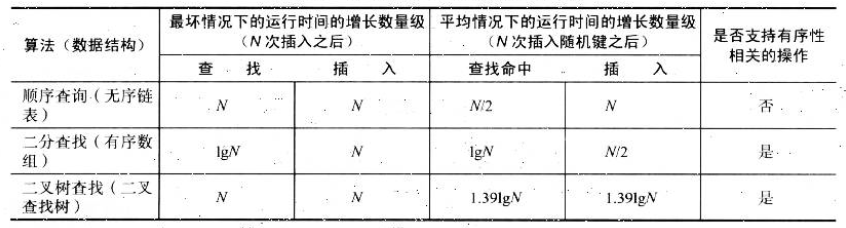
1.順序查找 在查找中我們一個一個順序的遍歷表中的所有鍵並使用equals()方法來查找匹配的鍵。 優點:對數組的結構沒有特定的要求,可以使用數組或者鏈表實現,演算法簡單。 缺點:當數組個數n較大時,效率低下。 時間複雜度:查找命中時,最大時間複雜度是O(n),最小時間複雜度是O(1),平均時間複雜度 ...
1.順序查找
在查找中我們一個一個順序的遍歷表中的所有鍵並使用equals()方法來查找匹配的鍵。
優點:對數組的結構沒有特定的要求,可以使用數組或者鏈表實現,演算法簡單。
缺點:當數組個數n較大時,效率低下。
時間複雜度:查找命中時,最大時間複雜度是O(n),最小時間複雜度是O(1),平均時間複雜度是O(n/2);未命中時,總需要O(n)次比較。
向一個空表中插入N個不同的件需要N2次比較。
2.基於有序數組的二分查找
在查找時,我們先將被查找的鍵和子數組的中間鍵比較。如果被查找的鍵小於中間鍵,我們就在左子數組中繼續查找,如果大於我們就在右子數組中繼續查找,否則中間鍵就是我們要找的鍵。
非遞歸的二分查找:

//非遞歸
public int rank(Key key)
{
int lo = 0, hi = N - 1;
while(lo <= hi)
{
int mid = lo + (hi - lo) / 2;
int com = key.compareTo(keys[mid]);
if(com < 0)
{
hi = mid - 1;
}
else if(com > 0)
{
lo = mid + 1;
}
else
{
return mid;
}
}
return lo;
}
View Code
非遞歸的二分查找:

//遞歸
public int rank(Key key,int lo,int hi)
{
if(hi < lo)
{
return lo;
}
int mid = lo + (hi - lo) / 2;
int com = key.compareTo(keys[mid]);
if(com < 0)
{
return rank(key,lo,mid-1);
}
else if(com > 0)
{
return rank(key,mid + 1,hi);
}
else
{
return mid;
}
}
View Code
一般情況下二分查找都比順序查找快得多,對於一個靜態表(不允許插入)來說,將其在初始化時就排序是值得的。

對於二分查找而言,如果表太大,動態表(插入操作較多)是不適用的。在上表所示,二分查找演算法在插入的時候成本依然是O(n)級別。
核心的問題在於我們能否找到能夠同時保證查找和插入操作都是對數級別的演算法和數據結構。答案是令人興奮的“可以”!
我們如何能夠實現這個目標呢?要支持高效的插入操作,我們似乎需要一種鏈式結構。但單鏈接的鏈表是無法使用二分查找法的,
因為二分查找的高效來自於能夠快速通過索引取得任何子數組的中間元素(但得到一條鏈表的中間元素的唯一方法只能是沿鏈表遍歷)。
為了將二分查找的效率和鏈表的靈活性結合起來,我們需要更加複雜的數據結構。能夠同時擁有兩者的就是二叉查找樹。
以上詳細內容可參考博文:淺談演算法和數據結構: 六 符號表及其基本實現
3.二叉查找樹
二叉查找樹:是一棵二叉樹,其中每個結點都含有一個鍵以及相關聯的一個值且每個結點的鍵都大於其左子樹中的任意結點的鍵而小於其右子樹中的任意結點的鍵。
二叉查找樹的插入、查找、最大鍵最小鍵、向上取整和向下取整、範圍查找、刪除操作在 演算法(第四版)書中有很好的實現,其中的演算法思想非常值得學習。
可參考博文:淺談演算法和數據結構: 七 二叉查找樹
實現代碼:

public class BTS<Key extends Comparable<Key>,Value> {
//定義樹
public class Node
{
//左結點
private Node left;
//右結點
private Node right;
private Key key;
private Value value;
private int N;
public Node(Key key,Value value,int N)
{
this.key = key;
this.value = value;
this.N = N;
}
}
//根結點
private Node root;
//獲取樹的大小
public int size()
{
return size(root);
}
public int size(Node root)
{
if(root == null)
{
return 0;
}
return root.N;
}
//根據鍵獲取相關聯的值
public Value get(Key key)
{
return get(root,key);
}
public Value get(Node root,Key key)
{
if(root == null)
{
return null;
}
//判斷被查找鍵與當前結點鍵的大小
int cmp = root.key.compareTo(key);
//若被查找的鍵小於當前結點鍵,則繼續在當前結點的左子樹上查找
if(cmp < 0)
{
return get(root.left,key);
}
//若被查找的鍵大於當前結點的鍵,則繼續在當前結點的右子樹上查找
else if(cmp > 0)
{
return get(root.right,key);
}
//若相等,則返回相關聯的值
else
{
return root.value;
}
}
//向樹中添加鍵值對,並插入在合適的位置
public void put(Key key,Value value)
{
root = put(root,key,value);
}
public Node put(Node root,Key key,Value value)
{
if(root == null)
{
return new Node(key,value,1);
}
//插入的鍵與當前結點的鍵進行比較
int cmp = root.key.compareTo(key);
//若插入的鍵小於當前結點的鍵,則繼續向當前結點的左子樹中插入
if(cmp < 0)
{
root.left = put(root.left,key,value);
}
//若插入的鍵大於當前結點的鍵,則繼續向當前結點的右子樹中插入
else if(cmp > 0)
{
root.right = put(root.right,key,value);
}
//若查找到相同的鍵時,則將插入的鍵相關聯的值替換掉當前結點的鍵相關聯的值
else
{
root.value = value;
}
//將樹的大小加1
root.N = size(root.left) + size(root.right) + 1;
return root;
}
//獲取樹中最小的鍵
public Key min()
{
return min(root).key;
}
public Node min(Node x)
{
//若當前結點的左子樹為空時,則表明當前結點的鍵是樹中最小的鍵,返回該結點
if(x.left == null)
{
return x;
}
//否則繼續向當前結點的左子樹查找
return min(x.left);
}
//對給定鍵進行向下取整
//如果給定的鍵小於二叉查找樹的根結點的鍵,
//那麼小於等於key的最大鍵floor(key)一定在根結點的左子樹中;
//如果給定的鍵大於二叉查找樹的根結點的鍵,
//那麼只有當根結點右子樹中存在小於等於key的結點時,
//小於等於key的最大鍵才會出現在右子樹中,
//否則根結點就是小於等於key的最大鍵。
public Key floor(Key key)
{
Node x = floor(root,key);
if(x == null)
{
return null;
}
return x.key;
}
public Node floor(Node root,Key key)
{
if(root == null)
{
return null;
}
int cmp = key.compareTo(root.key);
//如果相等,則返回當前結點
if(cmp == 0)
{
return root;
}
//給定鍵小於當前結點的鍵時,繼續遞歸查找當前結點的左子樹
else if(cmp < 0)
{
return floor(root.left,key);
}
//給定鍵大於當前結點的鍵時,向當前結點的右子樹繼續遍歷,並將結點返回給t
Node t = floor(root.right,key);
//若t不為空,則說明右子樹中存在小於等於key的最大鍵,返回t
if(t != null)
{
return t;
}
//否則返回當前結點
else
{
return root;
}
}
//查找排位為key的鍵
public Key select(int key)
{
return select(root,key).key;
}
public Node select(Node x,int key)
{
if(x == null)
{
return null;
}
int size = size(x.left);
//如果key小於左子樹中的結點數size,那麼就繼續遞歸地在左子樹中查找排名為k的鍵
if(key < size)
{
return select(x.left,key);
}
//如果key大於size,我們就遞歸地在右子樹中查找排名為k-t-1的鍵
else if(key > size)
{
return select(x.right,key - size - 1);
}
//如果size等於key,返回當前根結點中的鍵
else
{
return x;
}
}
//根據給定鍵返回鍵在樹中的排名
public int rank(Key key)
{
return rank(root,key);
}
public int rank(Node x,Key key)
{
if(x == null)
{
return 0;
}
int cmp = key.compareTo(x.key);
//如果給定鍵小於當前結點的鍵,則遞歸地向左子樹比較並返回該鍵在左子樹中的排名
if(cmp < 0)
{
return rank(x.left,key);
}
//如果給定鍵大於當前結點的鍵,則返回左子樹中的結點總數加上1(根結點)再加上右子樹中的排名(遞歸計算)
else if(cmp > 0)
{
return 1 + size(x.left) + rank(x.right,key);
}
//若相等,則返回當前結點左子樹中的結點總數
else
{
return size(x.left);
}
}
//刪除最小鍵
public void deleteMin()
{
deleteMin(root);
}
public Node deleteMin(Node x)
{
//若當前結點的左子樹為空,則返回當前結點的右子樹的結點
if(x.left == null)
{
return x.right;
}
//若當前結點的左子樹不為空,則繼續深入當前結點的左子樹直至遇到空左子樹
//進行回溯時將該結點的鏈接指向該結點的右子樹
x.left = deleteMin(x.left);
//重新計算樹的大小
x.N = size(x.left) + size(x.right) + 1;
return x;
}
//刪除給定鍵
public void delete(Key key)
{
root = delete(root,key);
}
public Node delete(Node x,Key key)
{
if(x == null)
{
return null;
}
int cmp = key.compareTo(x.key);
//若給定鍵小於當前結點的鍵,則繼續深入當前結點的左子樹
if(cmp < 0)
{
x.left = delete(x.left,key);
}
//若給定鍵大於當前結點的鍵,則繼續深入當前結點的右子樹
else if(cmp > 0)
{
x.right = delete(x.right,key);
}
//若相等
else
{
//如果當前結點的左子樹為空,則返回當前結點的右子樹結點
if(x.left == null)
{
return x.right;
}
//如果當前結點的右子樹為空,則返回當前結點的左子樹結點
if(x.right == null)
{
return x.left;
}
//否則的話:
//1.將指向即將被刪除的結點的鏈接保存為t
Node t = x;
//2.將x指向它的後繼結點min(t.right)
x = min(t.right);
//3.將x的右鏈接(原本指向一棵所有結點都大於x.key的二叉查找樹)指向deleteMin(t.right),也就是在
//刪除後所有的結點仍然都大於x.key的子二叉查找樹
x.right = deleteMin(t.right);
//4.將x的左鏈接(本為空)設為t.left(其下所有的鍵都小於被刪除的結點和它的後繼結點)
x.left = t.left;
}
//重新計算樹的大小
x.N = size(x.left) + size(x.right) + 1;
return x;
}
}
View Code
分析:使用二叉查找樹的演算法的運行時間取決於樹的形狀,而樹的形狀又取決於被插入的先後順序,在最好的情況下,一個含有N個節點的樹是完全平衡的,每個空鏈接到根節點的距離都是lgN。
最壞情況下,搜索路徑上可能有N個節點。就這個模型的分析而言,二叉查找樹和快速排序幾乎是”雙胞胎”,樹的根節點就是快速排序中的第一個切分元素。
二叉樹事先的良好性能依賴於其中的鍵的分佈足夠隨機以消除長路徑。對於快速排序,我們可以先將數組打亂,而對於符號表的API,我們無能為力,因為符號表的用例控制著各種操作的先後順序,
。最壞的情況是所有鍵按照順序或者逆序插入符號表。
這個問題依然是可以被解決的,因為還有平衡二叉查找樹,它能保證無論鍵的插入順序如何,樹的高度都將是總鍵數的對數。
4.平衡查找樹
我們希望能保持二叉查找樹的平衡性,所有查找都能在lgN次比較內結束。
4.1 2-3查找樹
為了保證樹的平衡性,我們需要一些靈活性,因此在這裡我們允許樹中的一個節點保存多個鍵。
首先我們引入2-3查找樹,2-3查找樹既有2-節點(一個鍵和兩條鏈接)又有3-節點(兩個鍵和三條鏈接),當然這隻是過渡,過後再引入紅黑樹和B-樹。

和標準的二叉查找樹由上向下生長不同,2-3樹的生長是由下向上的(節點的分解),也正是因為這樣,2-3樹才保證了平衡。
具體可參考博文:淺談演算法和數據結構: 八 平衡查找樹之2-3樹
2-3樹的實現操作是並不方便的,我們需要維護兩種不同類型的節點,將鏈接和其他信息從一個節點複製到另一個節點,將節點從一種數據類型轉換到另一種數據類型等等,
實現這些不僅需要大量的代碼,而且他們所產生的額外開銷可能會使演算法比標準的二叉查找樹更慢。
實際上我們只需要花一點代價就能解決這個問題,就是下麵我們引入的紅黑樹。
4.2 紅黑二叉查找樹
紅黑二叉查找樹的基本思想是用標準的二叉查找樹(完全有2-節點構成)和一些額外的信息(替換3-節點)來表示2-3樹。
我們講樹中的鏈接分為兩種類型:左斜的紅色鏈接將兩個2-節點連接起來構成一個3-節點,黑鏈接則是2-3樹中的普通鏈接。
對於任意的2-3樹,只要對節點進行轉換,我們都可以立即派生出一顆對應的二叉查找樹。
等價定義:
①紅鏈接均是左鏈接
②沒有任何一個節點同時和兩條紅鏈接相連
③ 該樹是完美黑色平衡的,即任意空鏈接到根節點的路徑上的黑鏈接數量相同。

通過旋轉和顏色翻轉這些平衡化操作,讓一個紅黑樹保持平衡。紅黑樹並不追求“完全平衡”——它只要求部分地達到平衡要求,降低了對旋轉的要求,從而提高了性能。
具體可參考下麵這篇博文:
淺談演算法和數據結構: 九 平衡查找樹之紅黑樹
紅黑樹應用:
TreeMap 和 TreeSet 是 Java Collection Framework 的兩個重要成員,其中 TreeMap 是 Map 介面的常用實現類,而 TreeSet 是 Set 介面的常用實現類。
雖然 HashMap 和 HashSet 實現的介面規範不同,但 TreeSet 底層是通過 TreeMap 來實現的,因此二者的實現方式完全一樣。而 TreeMap 的實現就是紅黑樹演算法。
對於 TreeMap 而言,由於它底層採用一棵“紅黑樹”來保存集合中的 Entry,這意味這 TreeMap 添加元素、取出元素的性能都比 HashMap 低:當 TreeMap 添加元素時,需要通過迴圈找到新增 Entry 的插入位置,因此比較耗性能;當從 TreeMap 中取出元素時,需要通過迴圈才能找到合適的 Entry,也比較耗性能。
但 TreeMap、TreeSet 比 HashMap、HashSet 的優勢在於:TreeMap 中的所有 Entry 總是按 key 根據指定排序規則保持有序狀態,TreeSet 中所有元素總是根據指定排序規則保持有序狀態。




