Luhn檢驗和驗證 Luhn公式是一種廣泛使用的系統,用於對標識號進行驗證。它根據原始標識號,把每隔一個數字的值擴大一倍。然後把各個單獨數字的值加在一起(如果擴大一倍後的值為2個數字,就把這兩個數字分別相加)。如果相加之後可以被10整除,那麼這個標識號就是合法的。 編寫一個程式,接受一個任意長度的標 ...
Luhn檢驗和驗證
Luhn公式是一種廣泛使用的系統,用於對標識號進行驗證。它根據原始標識號,把每隔一個數字的值擴大一倍。然後把各個單獨數字的值加在一起(如果擴大一倍後的值為2個數字,就把這兩個數字分別相加)。如果相加之後可以被10整除,那麼這個標識號就是合法的。
編寫一個程式,接受一個任意長度的標識號,並根據Luhn公式確定這個標識號是否合法。這個程式在讀取下一個字元之前必須處理之前所讀取的那個字元。
過程有些複雜,在此上傳一張圖片以供各位理解:

記住:最終標識號的檢驗和應該能夠被10整除,或者說應該以0結尾。
接下來我們一起分解問題
- 知道哪些數字需要擴大一倍。
- 對擴大一倍後大於等於10的數字,根據他們的單獨數字進行處理。
- 知道已經到達了標識號的尾部。
- 分別讀取每個數字。
(註:我們不需要按照特定的順序處理這些問題。)
首先,我們處理擴大一倍後大於或等於10的數:
如果我們從單獨的數字0~9開始並把它們擴大一倍,最大值將是18。因此,一共只有兩種可能性:如果擴大一倍後的值為單個數字,就不需要再做處理;如果擴大一倍後的值大於或等於10,它的範圍肯定在10~18之間,因此第一個數字總是為1.我們通過一個代碼來驗證一下:
1 int digit; 2 printf("Enter a single digit number,0-9:"); 3 scanf("%d",&digit); 4 int doubledDigit = digit * 2; //程式讀取數字,並把它的值擴大一倍 5 int sum; 6 if(doubledDigit >= 10) 7 sum = 1 + doubledDigit % 10; //求和計算 8 else 9 sum = doubledDigit; 10 printf("Sum of digits in doubled number:%d\n",sum); //輸出求和結果
驗證結果如下:

我們可以把這段代碼轉化為一個短小的函數,這樣就可以簡化未來的代碼了。(是不是很有遠見呢?)
1 int doubleDigitValue(int digit) 2 { 3 int doubledDigit = digit * 2; //程式讀取數字,並把它的值擴大一倍 4 int sum; 5 if(doubledDigit >= 10) 6 sum = 1 + doubledDigit % 10; //求和計算 7 else 8 sum = doubledDigit; 9 return sum; 10 }
現在,我們讀取標識號的單獨數字:
如果我們以數值類型(例如int)的形式讀取標識號,將會讀取一個長長的數,需要處理很多事情。另外,可以讀取的最大整數也是有限制的。但在該問題中,標識號可以是任意長度的。因此,我們必須逐字元讀取。這意味著我們要知道怎樣讀取一個表示數字的字元並把它轉換為整數類型,以便對它進行數學運算。來看以下代碼:
1 char digit; 2 printf("Enter a one-digit number:"); 3 scanf("%c",&digit); 4 int sum = digit; 5 printf("Is the sum of digits:%d?\n",sum);
運行結果為:

字元7是以字元碼值55存儲的,因此當我們把這個字元作為整數時,得到的結果就是55.
因此,我們需要一種機制把字元7轉換為整數7。
我們可以創建一張表,其中包含原值和目標值,還有兩值之間的誤差。
| 字元 | 字元碼 | 目標整數值 | 差 |
| 0 | 48 | 0 | 48 |
| 1 | 49 | 1 | 48 |
| 2 | 50 | 2 | 48 |
| 3 | 51 | 3 | 48 |
| 4 | 52 | 4 | 48 |
| 5 | 53 | 5 | 48 |
| 6 | 54 | 6 | 48 |
| 7 | 55 | 7 | 48 |
| 8 | 56 | 8 | 48 |
| 9 | 57 | 9 | 48 |
字元碼和目標整數值之差始終是48,因此我們需要做的就是使字元碼減去這個值。而48正好是0的字元碼,所以我們可以採用一種更通用、更容易理解的解決方案:就是減去字元0的字元碼而不是減去像48這樣預先確定的值:
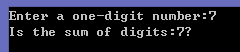
1 char digit; 2 printf("Enter a one-digit number:"); 3 scanf("%c",&digit); 4 int sum = digit - '0'; 5 printf("Is the sum of digits:%d?\n",sum);
運行結果為:
現在,我們轉到問題的下一部分,判斷哪些數字需要擴大一倍:
我們可以先試著把長度限製為6,則我們只需要讀取6個數字,對它們進行求和,然後判斷它們的和是否被10所整除,代碼如下:
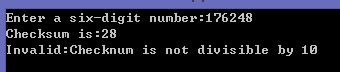
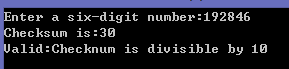
1 char digit; 2 int checksum = 0; 3 printf("Enter a six-digit number:"); 4 for(int position = 1;position <= 6;position++){ 5 scanf("%c",&digit); 6 checksum += digit - '0'; 7 } 8 printf("Checksum is:%d\n",checksum); 9 if(checksum%10 == 0) 10 printf("Valid:Checknum is divisible by 10\n"); 11 else 12 printf("Invalid:Checknum is not divisible by 10\n");
運行結果為:
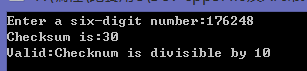
現在,我們需要為實際的Luhn檢驗公式增加邏輯,把從左邊開始位置為奇數的數字擴大一倍。我們可以使用求摸操作符(%)確定奇數和偶數的位置,因為偶數的定義是它能夠被2所整除。因此如果表達式位置%2的結果是1,這個位置就是奇數,應該把它擴大一倍。順便插一句,在擴大一倍後,如果結果大於或等於10,還需要對這個結果的各個數字進行求和。代碼如下(只需把for迴圈那改一下):
1 for(int position = 1;position <= 6;position++){ 2 scanf("%c",&digit); 3 if(position%2 == 0) checksum += digit - '0'; 4 else checksum += doubleDigitValue(digit - '0'); 5 }
運行結果為:
到目前為止,我們在這個問題上已經取得很大的進展,但還需要完成一些步驟才能為任意長度的標識號編寫代碼。為了最終解決這個問題,我們需要採用分治法。
先考慮怎樣處理長度為任意偶數的標識號。
我們所面臨的第一個問題是怎樣確定已經到達了標識號的末尾。如果用戶輸入了一個多位的標識號又按下了Enter鍵表示結束,並且我們是逐個字元讀取輸入的,那麼在最後一個數字之後所讀取的字元是什麼呢?我們不妨用代碼來試驗一下:
1 printf("Enter a number:"); 2 char digit; 3 while(1){ 4 scanf("%c",&digit); 5 printf("%d\n",int(digit)); 6 }
運行結果為:
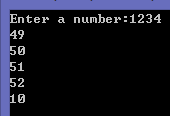
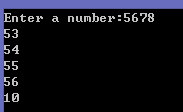
輸入1234,結果是49 50 51 52 10(結果基於ASCII碼)。從運行結果中可以看出,10就是我們所尋找的結果,所以我們可以在前面的代碼中用一個while迴圈代替for迴圈:
1 //處理任意偶數長度的標識號 2 char digit; 3 int checksum = 0; 4 int position = 1; 5 printf("Enter a number with an even number of digits:"); 6 scanf("%c",&digit); //讀取第一個值 7 while(digit != 10){ //用來檢查字元碼的值是否為行末符 8 if(position%2 == 0) //偶數位判斷 9 checksum += digit - '0'; 10 else checksum += 2 * (digit - '0'); 11 scanf("%c",&digit); //讀取每個後續的值 12 position++; 13 } 14 printf("Checksum is:%d\n",checksum); 15 if(checksum%10 == 0) 16 printf("Valid:Checksum is divisible by 10\n"); 17 else 18 printf("Invalid:Checksum is not divisible by 10\n");
運行結果為:


現在已經解決了“怎樣確定已經到達了標識號的末尾”的問題。
要窮盡每種可能性,標識號的長度必須是奇數或者偶數。如果我們預先知道長度,就可以知道應該把奇數位的數字或者偶數位的數字擴大一倍。但是,在讀取完這個標識號之前,我們並不知道這個信息。在思考這個問題前,我們先來類比另外一個問題:
編寫一個程式,從用戶那裡讀取10個整數。在輸入了所有的整數之後,要求顯示這些數中正數或負數的數量。
編寫思路:需要一個對正數進行計數的變數,並用另一個變數對負數進行計數。當用戶在程式的最後指定了具體的請求時,只需顯示適當的變數作為響應即可。代碼如下:
1 int number; 2 int positiveCount = 0; 3 int negativeCount = 0; 4 for(int i = 1;i <= 10;i++){ 5 scanf("%d",&number); 6 if(number > 0) positiveCount++; //計數正值 7 if(number < 0) negativeCount++; //計數負值 8 } 9 char response; //選擇回答 10 printf("Do you want the (p)ositive or (n)egative count?"); 11 getchar(); //吞掉回車 12 scanf("%c",&response); 13 if(response == 'p') 14 printf("Positive Count is %d\n",positiveCount); 15 if(response == 'n') 16 printf("Negative Count is %d\n",negativeCount);
運行結果為:


這個類比的問題顯示了我們在解決Luhn檢驗和問題時所需要用到的方法:同時以兩種方式追蹤當前的檢驗和,分別是在標識符為奇數長度和偶數長度的情況下。當我們讀取完這個編號並確定了它的真正長度時,再選擇表示正確的檢驗和的變數。
現在,我們可以把所有的代碼都集中在一起,來解決這個問題了。
開始AC!!!
1 char digit; 2 int oddLengthChecksum = 0; 3 int evenLengthChecksum = 0; 4 int position = 1; 5 printf("Enter a number:"); 6 scanf("%c",&digit); 7 while(digit != 10){ 8 if(position%2 == 0){ 9 oddLengthChecksum += doubleDigitValue(digit - '0'); 10 evenLengthChecksum += digit - '0'; 11 } 12 else{ 13 oddLengthChecksum += digit - '0'; 14 evenLengthChecksum += doubleDigitValue(digit - '0'); 15 } 16 scanf("%c",&digit); 17 position++; 18 } 19 int checksum; 20 if((position - 1)%2 == 0) checksum = evenLengthChecksum; 21 else checksum = oddLengthChecksum; 22 printf("Checksum is:%d\n",checksum); 23 if(checksum%10 == 0) 24 printf("Valid:Checknum is divisible by 10\n"); 25 else 26 printf("Invalid:Checknum is not divisible by 10\n");
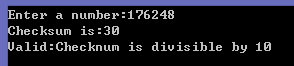
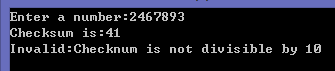
運行結果為:

尾聲:這篇博文寫了一晚上,視力開始模糊了,而且還有一些頭痛的癥狀,可能是昨天下午出去玩吹涼風了。不過今天還是很開心的,看著一個完整的演算法被我們切成一小塊一小塊的細緻分析和代碼檢驗,沉浸於其中,一點點的接近真相,我感到興奮和快樂!剛開始我還對函數調用和程式中的回車問題有所疑惑,不過在一位朋友的指點下我還是順利通過了。最重要的是,我對這個演算法也有了更深一步的瞭解與認識。
不得不承認,我開始喜歡上寫作了,那麼問題來了,寫作也會如期而至地喜歡上我嗎?



