散列表的具體實現就不多做介紹了,就是一個數組,每個下標存儲的是碰撞的元素的鏈表頭指針,如下圖所示: 下麵直接研究對用鏈接法散列的分析: 給定一個能存放n個元素的、具有m個槽位的散列表T,定義T的裝載因數α為n/m,即一個鏈中平均存儲的元素數。 用鏈接法散列的最壞情況性能很差:所有的n個關鍵字都散列到 ...
散列表的具體實現就不多做介紹了,就是一個數組,每個下標存儲的是碰撞的元素的鏈表頭指針,如下圖所示:

下麵直接研究對用鏈接法散列的分析:
給定一個能存放n個元素的、具有m個槽位的散列表T,定義T的裝載因數α為n/m,即一個鏈中平均存儲的元素數。
用鏈接法散列的最壞情況性能很差:所有的n個關鍵字都散列到同一個槽中,從而產生出一個長度為n的鏈表。這時,最壞情況下查找的時間為O(n),再加上計算散列函數的時間,這麼一來就和用一個鏈表來鏈接所有的元素差不多了。顯然我們並不是因為散列表的最壞情況性能差才用它的。
散列方法的平均性態依賴於所選取的散列函數h在一般情況下,將所有的關鍵字分佈在m個槽位上的均勻程度。這會兒我們先假定任何元素散列到m個槽中每一個的可能性是相同的,且與其他元素已被散列到什麼位置上是獨立無關的。稱這個假設為簡單一致散列。
對於j=0,1,...,m-1,列表T[j](每個槽位對應的鏈表)的長度用nj表示,這樣有:

nj的平均值為E[nj]=α=n/m。
假定可以在O(1)時間內計算出散列值h(k)(數組下標),從而查找具有關鍵字為k的元素的時間線性地依賴於表T[h(k)]的長度nh(k)。先不考慮計算散列函數和定址槽h(k)的O(1)時間,我們來看看查找演算法期望查找的元素數,即為比較元素的關鍵字是否為k而檢查的表T[h(k)]中的元素數。分兩種情況來考慮。在第一種情況中,查找不成功:表中沒有一個元素的關鍵字為k。在第二種情況中,查找成功地找到關鍵字為k的元素。
定理11.1 對一個用鏈接技術來解決碰撞的散列表,在簡單一致散列的假設下,一次不成功查找的期望時間為O(1+α)。
證明:在簡單一致散列的假設下,任何尚未被存儲在表中的關鍵字k都是等可能地被散列到m個槽的任一個之中。因而,當查找一個關鍵字k時,在不成功的情況下,查找的期望時間就是查找至鏈表T[h(k)]末尾的期望時間,這一時間的期望長度為E[nh(k)]=α。於是,一次不成功的查找平均要檢查α個元素,所需的總時間(包括計算h(k)的時間)為O(1+α)。
對於成功的查找來說,情況略有不同,這是因為每個鏈表並不是等可能地被查找到的。某個鏈表被查找到的概率與它所包含的元素數成正比。然而,期望的查找時間仍然是O(1+α)。
定理11.2 在簡單一致散列的假設下,對於用鏈接技術解決碰撞的散列表,平均情況下一次成功的查找需要O(1+α)時間。
證明:假設要查找的關鍵字是表中存放的n個關鍵字中任何一個的可能性是相同的。在對元素x的一次成功的查找中,所檢查的元素數比x所在的鏈表中,出現在x前面的元素數多1。在該鏈表中,出現在x之前的元素都是在x之後插入的,這是因為新的元素都是在表頭插入的。為了確定所查找元素的期望數目,對x所在的鏈表中,在x之後插入到表中的期望元素數加1,再對錶中的n個元素x取平均。設xi 表示插入到表中的第i 個元素,i=1,2,...,n,並設ki=key[xi]。對關鍵字ki和kj,定義指示器隨機變數Xij=I{h(ki)=h(kj)}。在簡單一致散列的假設下,有Pr{h(ki)=h(kj)}=1/m,從而根據引理5.1,有E[Xij]=1/m。於是,在一次成功的查找中,所檢查元素的期望數目為
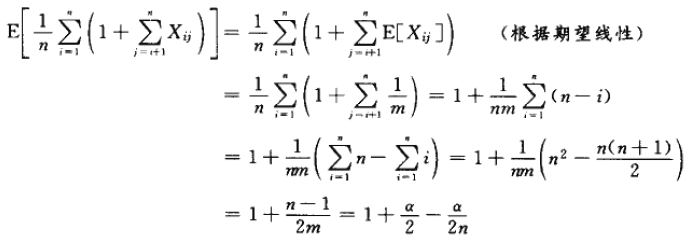
這裡有幾點註意:
1.根據離散數學,計算一個演算法在平均狀態下的計算複雜性,可以轉變成計算一個隨機變數的期望值。設一個實驗的樣本空間是可能輸入aj(j=1,2,...,n)的集合,且令隨機變數X對aj 賦值是aj 作為輸入時該演算法用到的操作次數。基於我們對輸入的瞭解,對每個可能的輸入aj 賦給一個概率p(aj)。那麼該演算法在平均狀態下的複雜性是
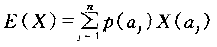
2.根據證明的第一句可知每個可能的輸入的概率為1/n。也就是說x等於表中第i 個元素的概率是1/n。
3.指示器隨機變數Xij=I{h(ki)=h(kj)}的含義是如果i 和j 散列在同一個槽位當中,也就是在同一個鏈表中時,加1次。
因此,綜上所述,在x之後插入到表中的所檢查元素的總數目為:
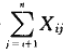
演算法在平均狀態下的所檢查元素的總數目為:
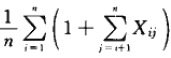
最後再計算這個式子的期望值就能得出所檢查元素的期望數目。於是,一次成功的查找所需的全部時間(包括計算散列函數的時間)為O(2+α/2-α/2n)=O(1+α)。



