用菜鳥的思維學習演算法 -- 馬桶排序、冒泡排序和快速排序 【博主】反骨仔 【來源】http://www.cnblogs.com/liqingwen/p/4994261.html 馬桶排序 一、場景：期末考試完了，老師要將同學們的分數從高到低排序。假設班上有 5 名同學，分別考了 5 分、3 分、5 ...
用菜鳥的思維學習演算法 -- 馬桶排序、冒泡排序和快速排序
【博主】反骨仔 【來源】http://www.cnblogs.com/liqingwen/p/4994261.html
馬桶排序
一、場景：期末考試完了，老師要將同學們的分數從高到低排序。假設班上有 5 名同學，分別考了 5 分、3 分、5 分、2 分和 8 分【滿分：10 分】，排序後的結果就是 8 5 5 3 2，現在，讓我們先思考 10 分鐘吧！ 二、思路： （1）先創建一個數組 int scores[11]，就有 scores[0]~scores[10] 共 11 個變數。我們用變數值為 0 表示沒有人得到該分數，即 scores [0]=0 表示沒有人得 0 分，scores [10]=0 表示沒有人得 10 分，而 scores [8]=1 表示有一個人得到 8 分。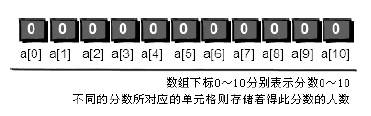
（2）第 1 個數為 5，所以在 scores[5]=0 的基礎上+1，即 scores[5]=1 表示有 1 人得到 5 分
（3）第 2 個數為 3，所以在 scores[3]=0 的基礎上+1，即 scores[3]=1 表示有 1 人得到 3 分
（4）第 3 個數為 5，所以在 scores[5]=1 的基礎上+1，即 scores[5]=2 表示有 2 人得到 5 分
... ...
（5）依此類推，處理第 4 和第 5 個數，最終的結果圖如下：
（6）我們發現，scores[0]~scores[10] 內對應的值就是 0~10 分中每個分數所出現的次數。現在，只需將結果列印即可，出現幾次就印表機次。
我們暫且稱它為“馬桶排序”，這個演算法就相當於有 11 個馬桶，編號從 0~10。每出現一個數，就在對應編號的馬桶中放一個旗子。
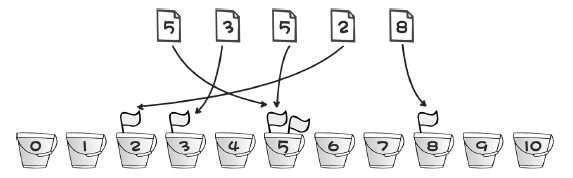三、思考：現在分別有 5 個人的名字和分數：小A 5、小二 3、小三 5、小妞 2 和王大錘 8，請按照分數從高到低，輸出他們的名字？
【特點】
假設需要排序的範圍 0~20000000，則需要 new int[20000001]，非常浪費空間，即便只給 2 個數排序（1,19999999 ）;
如果排序的數是小數也不行，如：3.141 5926 5358 9793 2384 6264 3383 2795 0238；
冒泡排序
一、基本思想：每次比較相鄰的兩個 元素，按需調整順序 二、題目：要求將 12 35 99 18 76 這 5 個數進行從大到小排序 三、思路： （1）先比較第 1 位和第 2 位的大小，12<35，因為希望越小越靠後，所以要調整兩者順序，交換後的結果：35 12 99 18 76 （2）現在比較第 2 位和第 3 位的大小，12<99，所以需要交換位置，交換後的結果為：35 99 12 18 76 （3）接著比較第 3 位和第 4 位的大小，12<18，交換後的結果為：35 99 18 12 76 （4）最後比較第 4 位和第 5 位的大小，12<76，交換後的結果為：35 99 18 76 12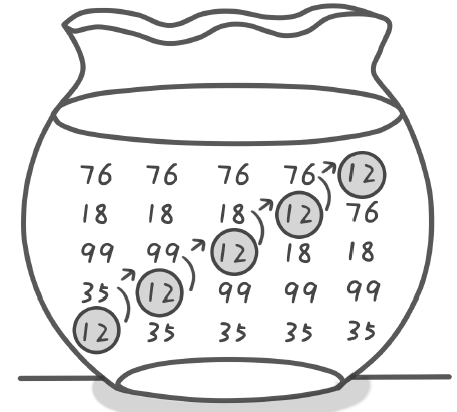
（5）經過 4 次後我們發現 5 個數中最小的一個數已經就位，每將一個數歸位我們稱其為“一趟”；
（6）現在我們開始第二趟，目標將第 2 小的數歸位，根據之前邏輯，還是從第 1 個數和第 2 個數開始比較上：
35 99 18 76 12 --①--> 99 35 18 76 12 --②--> 99 35 18 76 12 --③--> 99 35 76 18 12
在第一趟比較就知道第 5 位是最小的，所以第 4 位不用和第 5 位比較，這一趟只需比較 3 次
（7）第3趟：99 35 76 18 12 --> 99 35 76 18 12 --> 99 76 35 18 12 （比較 2 次）
（8）第4趟：99 76 35 18 12 --> 99 76 35 18 12 ,有4個數已經就位，那麼最後一個數無須比較，它就是最大的
【總結】如果有 n 個數進行排序，只需將 n-1 個數歸位，即要進行 n-1 趟操作，而每一趟開始都從第 1 位進行相鄰的兩個數 進行比較，將小的那個數放在後面，已經歸位的就不用進行比較。
【特點】冒泡演算法的核心部分是雙重嵌套迴圈，可以看出時間複雜度是 O(N²)，這是一個非常高的時間複雜度。
快速排序
一、場景：對 6 1 2 7 9 3 4 5 10 8 這 10 個數進行排序 二、思路： 先找一個基準數（一個用來參照的數），為了方便，我們選最左邊的 6，希望將 >6 的放到 6 的右邊，<6 的放到 6 左邊。如：3 1 2 5 4 6 9 7 10 8 先假設需要將 6 挪到的位置為 k，k 左邊的數 <6，右邊的數 >6 （1）我們先從初始數列“6 1 2 7 9 3 4 5 10 8 ”的兩端開始“探測 ”，先從右邊往左找一個 <6 的數，再從左往右找一個 >6 的數，然後交換。我們用變數 i 和變數 j 指向序列的最左邊和最右邊。剛開始時最左邊 i=0 指向 6，最右邊 j=9 指向 8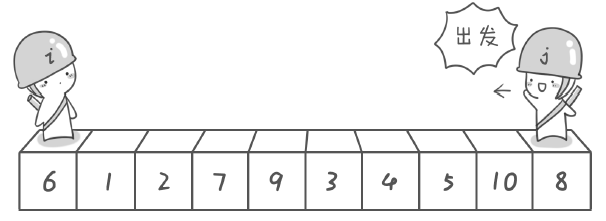
（2）現在設置的基準數是最左邊的數，所以序列先右往左移動（j--），當找到一個 <6 的數（5）就停下來。接著序列從左往右移動（i++），直到找到一個 >6 的數又停下來（7）；
（3）兩者交換，結果：6 1 2 5 9 3 4 7 10 8；
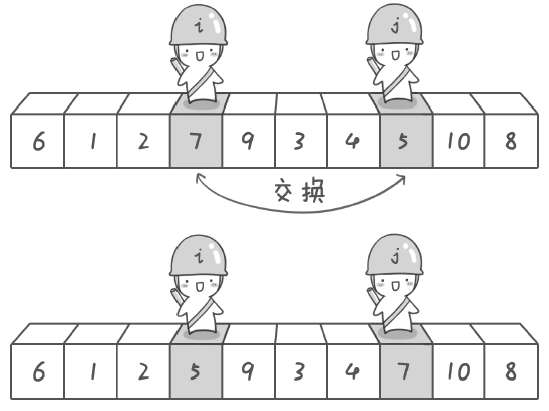（4）j 的位置繼續向左移動（友情提示：每次都必須先從 j 的位置出發），發現 4 滿足要求，接著 i++ 發現 9 滿足要求，交換後的結果：6 1 2 5 4 3 9 7 10 8；
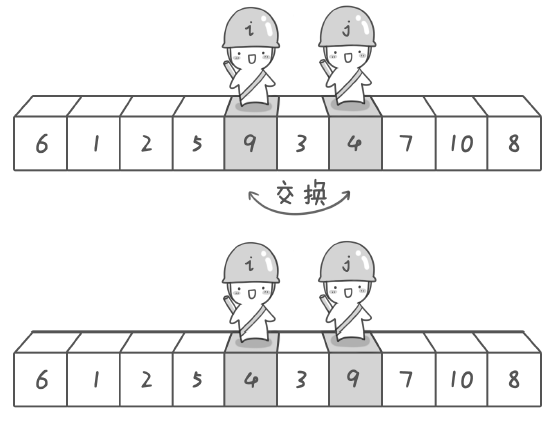
（5）目前 j 指向的值為 9，i 指向的值為 4，j-- 發現 3 符合要求，接著 i++ 發現 i=j，說明這一輪移動結束啦。現在將基準數 6 和 3 進行交換，結果：3 1 2 5 4 6 9 7 10 8；現在 6 左邊的數都是 <6 的，而右邊的數都是 >6 的，但游戲還沒結束
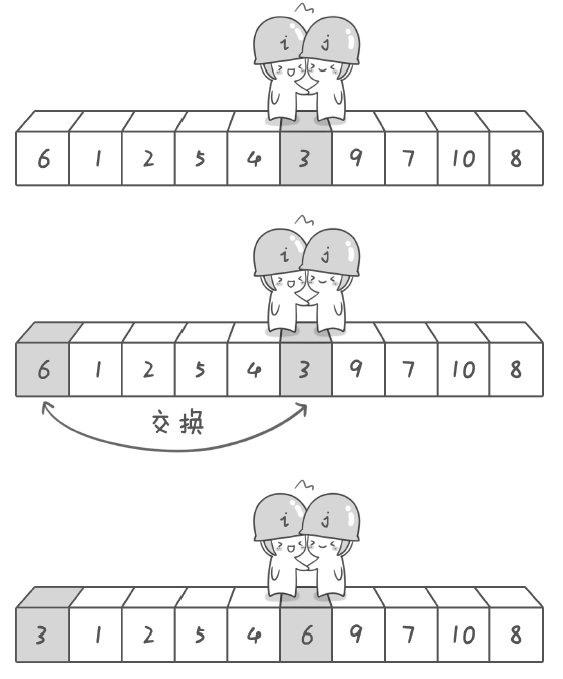（6）我們將 6 左邊的數拿出來先：3 1 2 5 4，這次以 3 為基準數進行調整，使得 3 左邊的數 <3，右邊的數 >3，根據之前的模擬，這次的結果：2 1 3 5 4
（7）再將 2 1 摳出來重新整理，得到的結果： 1 2
（8）剩下右邊的序列：9 7 10 8 也是這樣來搞，最終的結果： 1 2 3 4 5 6 7 8 9 10
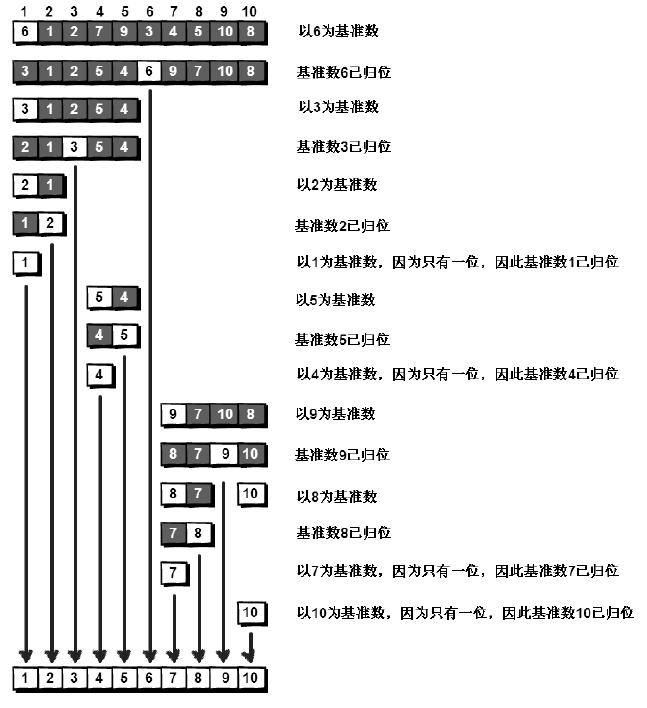【總結】快速排序的每一輪處理其實就是將這一輪的基準數歸位，當所有的基準數歸位，排序就結束啦
【參考】文字與插圖來源《啊哈！演算法》
