我用Awesome-Graphs看論文：解讀GraphBolt

這次向大家分享一篇流圖處理系統論文GraphBolt，看如何基於計算曆史的方式實現增量圖計算，並保證與全量圖計算語義的一致性。 ...

GraphBolt論文：《GraphBolt: Dependency-Driven Synchronous Processing of Streaming Graphs》

前面通過文章《論文圖譜當如是：Awesome-Graphs用200篇圖系統論文打個樣》向大家介紹了論文圖譜項目Awesome-Graphs，並分享了Google的Pregel、OSDI'12的PowerGraph、SOSP'13的X-Stream和Naiad。這次向大家分享一篇流圖處理系統論文GraphBolt，看如何基於計算曆史的方式實現增量圖計算，並保證與全量圖計算語義的一致性。

對圖計算技術感興趣的同學可以多做瞭解，也非常歡迎大家關註和參與論文圖譜的開源項目：

Awesome-Graphs：https://github.com/TuGraph-family/Awesome-Graphs
OSGraph：https://github.com/TuGraph-family/OSGraph

提前感謝給項目點Star的小伙伴，接下來我們直接進入正文！

摘要

GraphBolt通過抓取計算過程中的中間值依賴實現依賴驅動的增量計算，並保證了BSP語義。

1. 介紹

流圖處理的核心是動態圖，圖的更新流會頻繁地修改圖的結構，增量圖演算法會及時響應圖結構的變更，生成最新圖快照的最終結果。因此，增量圖演算法的核心目標是最小化重覆計算。典型系統如：GraphIn、KickStarter、Differential Dataflow等。

GraphBolt通過依賴驅動的流圖處理技術最小化圖變更帶來的重覆計算。

描述並跟蹤迭代過程中產生的中間值的依賴關係。
圖結構變更時，根據依賴關係逐迭代地產生最終結果。

關鍵優化：

利用圖結構信息以及點上聚合值的形式，將依賴信息的規模從O(E)降低為O(V)。
支持依賴驅動的優化策略和傳統的增量計算的動態切換，以適應因剪枝導致依賴信息不可用的情況。
提供通用的增量編程模型支持將複雜聚合拆解為合併增量值的方式。

2. 背景與動機

2.1 流圖處理

流圖G會一直被ΔG更新流修改，ΔG包含了點/邊的插入/刪除，演算法S在最新的圖快照上迭代計算最終結果。為了保證一致性，迭代計算過程中的更新被分批寫入到ΔG，併在下次迭代開始前合併到G。

同步處理

BSP模型將計算分為多個迭代，當前迭代的計算只依賴於上次迭代計算的結果。這讓圖演算法的開發更簡單，並能清晰的推導收斂信息以及準確性驗證。因此，同步處理模型是大規模圖計算系統的首選。

增量計算

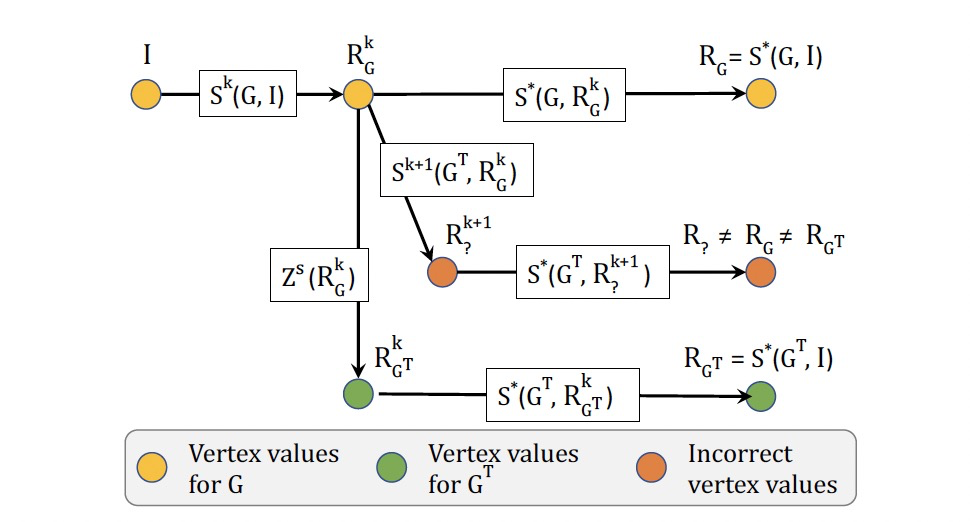
I：點初始值。
k：迭代次數。
Si(G, I)：以I為輸入的圖G上演算法S的第i次迭代。
S*(G, I)：以I為輸入的圖G上演算法的最後一次迭代。
RGi：圖G的第i次迭代結果。
RG：圖G的迭代結果。
GT：G+ΔG。
Zs：轉換函數，\(R_{G^T}^k = Z^s(R_G^k)\)。

2.2 問題：不正確的結果

如何在面向圖變更的流圖的增量計算中最小化重覆計算，而又保證同步處理的語義？

2.3 技術概覽

依賴驅動增量計算面臨的挑戰：

線上跟蹤依賴信息成本高，複雜度｜E｜。
- 基於點聚合值的方式，將複雜度降低到｜V｜。
- 現實圖一般是稀疏傾斜的，可以對依賴信息進行保守的剪枝。
處理複雜聚合計算的困難性。
- 開發通用增量編程模型將複雜聚合分解為增量的值變更。
- 簡單聚合，如sum、count可以直接表達，而無需走分解的流程。
計算感知的混合執行能力。
- 支持依賴驅動的優化策略和傳統的增量計算的動態切換。

3. 依賴感知處理

3.1 同步處理語義

基於圖結構定義值依賴關係：

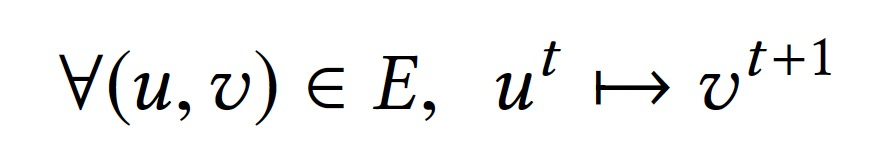
(u, v)：計算圖中任意邊。
ut：第t次迭代，點u的值。
->：依賴關係，後者依賴前者。

3.2 跟蹤值依賴關係

假設第L次迭代後，圖G被修改為GT，CL對應迭代L結束後的點值集合。為了保證結果的準確性，需要跟蹤計算過程中所有對CL有貢獻的點值信息。

令\(\mathcal{D}_G=(\mathcal{V}_D,\mathcal{E}_D)\)，則有：

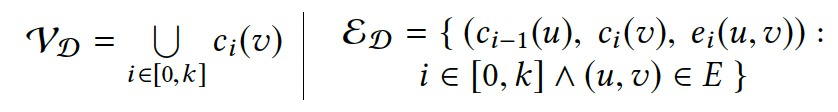
每次迭代，DG增加｜V｜個點和｜E｜和邊信息。空間複雜度O(|E|·t)。

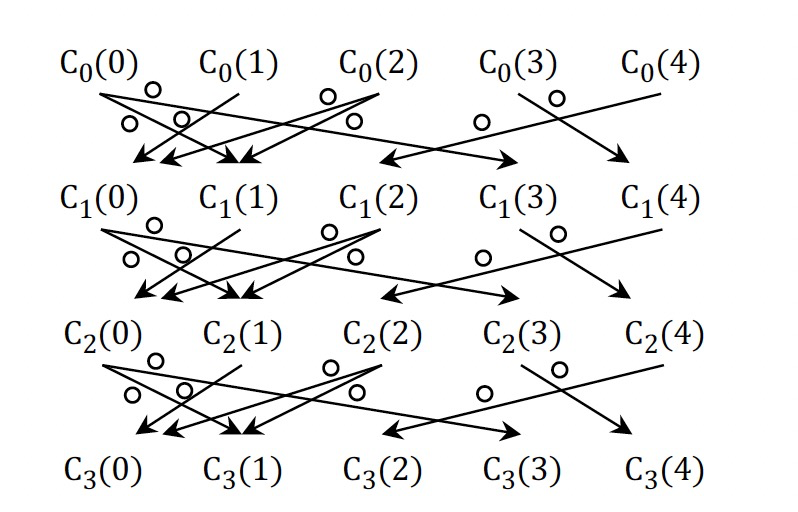
基於點聚合值跟蹤點依賴

一般點值計算分為兩個步驟。

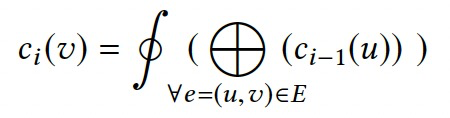
\(\bigoplus\)：聚合上次迭代的鄰居點的值。
\(\oint\)：根據聚合值計算點值。

令\(g_i(v)=\bigoplus_{\forall e=(u,v)\in E}(c_{i-1}(u))\)，\(\mathcal{A}_G=(\mathcal{V}_\mathcal{A},\mathcal{E}_\mathcal{A})\)，則有：

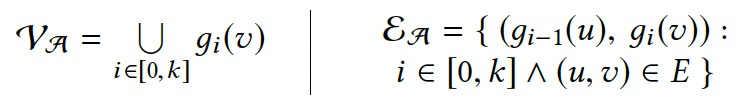
通過跟蹤點上的聚合值，而非單獨的點值，將空間複雜度降低到O(|V|·t)。

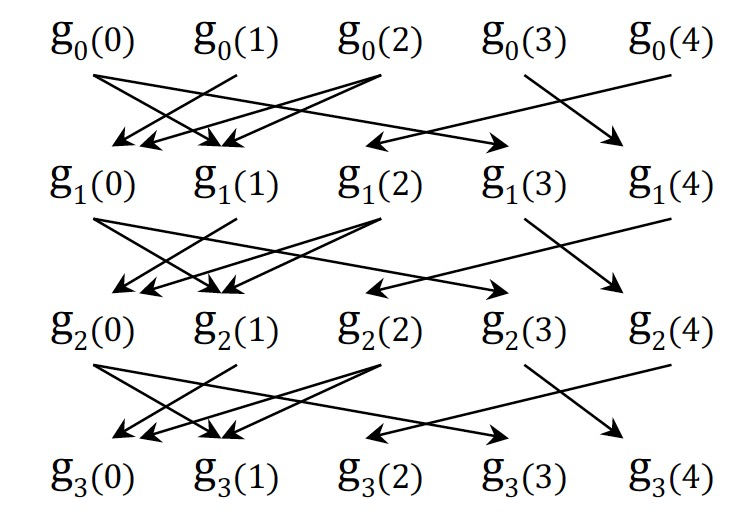
裁剪值聚合信息

現實圖上一般都是傾斜的，所以演算法最開始的時候大多數點值會發生變化，但隨著迭代的推進，更新點的數量將逐漸減少。

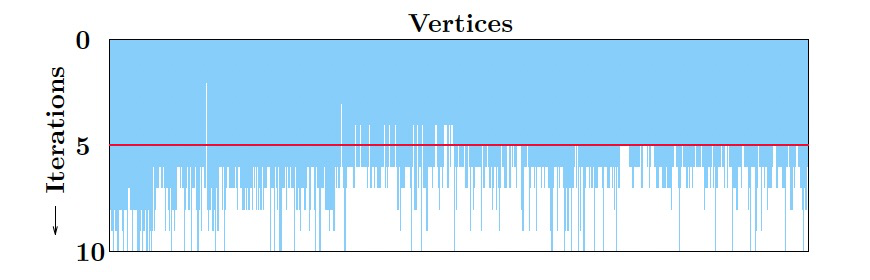
當點值穩定時，點上的聚合值也趨於穩定，這就為聚合值的依賴信息跟蹤提供了優化機會。

水平裁剪：當到達確定的迭代後，停止跟蹤聚合值，對應上圖中的紅線。
垂直裁剪：對於已經穩定的點值，將不再跟蹤聚合值，對應上圖中紅線上的白色區域。

3.3 依賴驅動的值優化

令Ea表示新增的邊，Ed表示刪除的邊，則有\(G^T=G \cup E_a \backslash E_d\)，對於依賴圖\(\mathcal{A}_G\)，如何轉換CL到CLT。

優化什麼？

每次迭代的優化動作有兩種：

Ea、Ed中邊的終點，對應的點值會被邊修改影響。
終點的鄰居，鄰居點值會在下次迭代中被優化。

例如，新增邊1->2時，聚合值的更新如上圖。其中實線表示值的傳播，虛線表示值的變化。
整個過程依賴於圖\(\mathcal{A}_G\)，聚合值變化來源於邊的修改。優化過程中涉及的計算遠小於在原圖上重新計算。

如何優化？

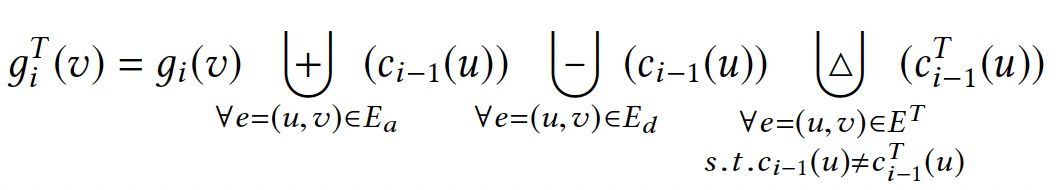
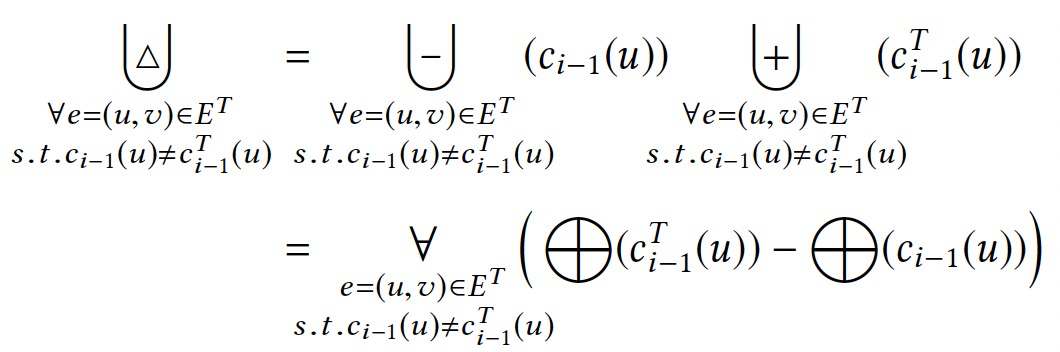
對於簡單的聚合操作，如sum、product，可以直接計算出變化的貢獻。但是對於複雜的聚合操作，如向量操作，就比較難以直接表示。

複雜聚合

對於MLDM演算法，如BP、ALS，將點值增量化就比較困難。將複雜聚合轉換為增量方式，可以分為兩步。

靜態拆解為簡單子聚合

複雜聚合可以被分解為多個簡單的子聚合，如ALS演算法。

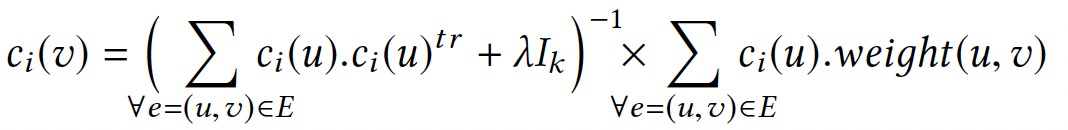
聚合值可以表示為：

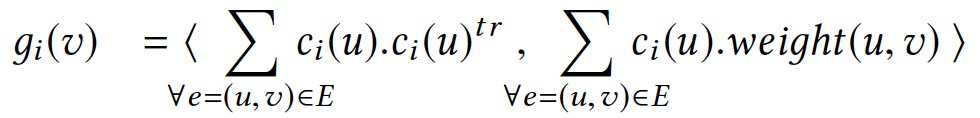
獨立貢獻的動態求值

子聚合對點值的計算發生在sum之前，會帶來重覆計算。因此需要獨立計算每個部分，再計算聚合的差異值。

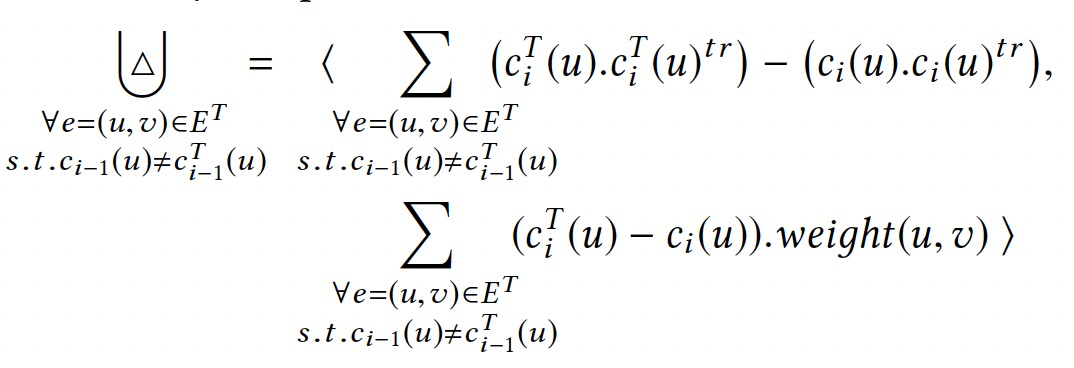
聚合屬性和擴展

三個增量聚合運算元（+、-、Δ）的特點：

運算元是可交換、可結合的。
運算元的定義域包含點上的聚合值以及邊上的關聯值。
運算元可以增量的處理單個輸入帶來的影響。

這類運算元屬於可分解的，如sum、count。

相對的則是不可分解的運算元，如max、min。對+操作可以可增量的，但是-和Δ則不可。
因此聚合值就退化為輸入點值的集合，實現方式是動態拉取輸入邊的值。

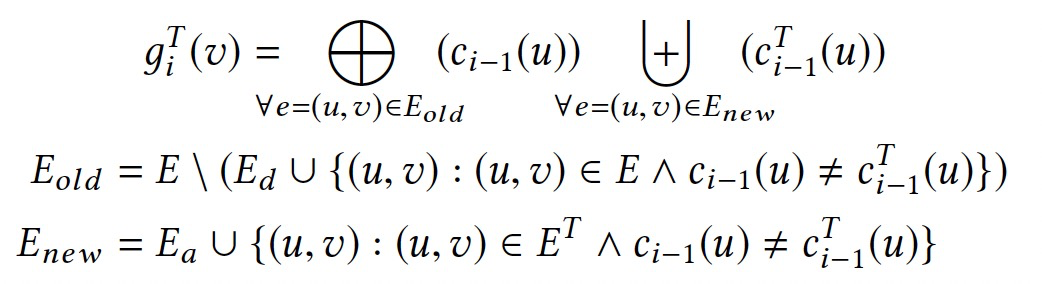
4. GraphBolt處理引擎

4.1 流圖和依賴佈局

點/邊的增加/刪除以以下兩種方式進行：

單個點/邊的變更。
批量點/邊的變更。

變更一旦生效會立即觸發值優化，在優化過程中的的變更會被緩存，併在接下來的優化步中繼續處理。
聚合值被維護在一個和點對應的數組中，保存了跨迭代的值數據。隨著計算過程，聚合值信息被更新並動態增長。

4.2 依賴驅動的處理模型

BP演算法使用restract+propagate模擬update。

PangeRank演算法直接定義propagate_delta實現update。

選擇性調度

GraphBolt只會在鄰居值更新後才會重新計算點值，並允許用戶指定選擇性調度的邏輯，如比較值變化的容忍範圍來決定是否發起重新計算。

計算感知的混合執行

水平裁剪導致超過指定迭代後，聚合值將不再有效，GraphBolt會動態切換為不帶值優化的增量計算模式。

4.3 保證同步語義

定理：使用依賴驅動的值優化方式，基於ci-1T(u)計算giT(v)可以滿足ET定義的依賴關係。

5 相關工作

流圖處理框架
- Tornado：在圖更新時，分叉執行用戶查詢。
- KickStarter：使用依賴樹增量修正單調圖演算法。
- GraphIn：使用固定大小的批處理動態圖，提供了5階段處理模型。
- Kineograph：基於pull/push模型實現圖挖掘的增量計算。
- STINGER：提出動態圖數據結構，為特定問題研發演算法。
圖快照的批處理
- Chronos：使用增量的方式實現跨快照的計算。
- GraphTau：維護快照上的值歷史記錄，通過值的回退實現數據修正。
- 靜態圖處理系統：處理離散的圖快照。
通用流處理
- 通用流處理系統：操作無邊界的非結構化數據流。
- Differential Dataflow：擴展了Timely Dataflow的增量計算，它強依賴於差分運算元。
增量演算法
- 增量PageRank
- Triangle Counting
- IVM演算法