利用兩個棧進行實現隊列的入隊和出隊操作 題目: 解題分析: 該題目需要藉助兩個棧來實現隊列的“入隊”和“出隊”,並封裝好了三個對應的函數。我們需要註意的是棧的特點是“先進後出",與隊列的”先進先出“的輸出並不一致。所以,我們要利用棧來輸出正常排序的序列,需要藉助類似取反的原理,例如 !false ...
利用兩個棧進行實現隊列的入隊和出隊操作
題目:

解題分析:
該題目需要藉助兩個棧來實現隊列的“入隊”和“出隊”,並封裝好了三個對應的函數。我們需要註意的是棧的特點是“先進後出",與隊列的”先進先出“的輸出並不一致。所以,我們要利用棧來輸出正常排序的序列,需要藉助類似取反的原理,例如 !false == true,而 !(!false) == false。
即我們需要現將元素存入棧s1,在對其執行出棧操作,此時我們得到元素的排列順序與初始相反。此時我們在將該元素序列存入棧s2,再次取出便能得到“先進先出”排列順序的元素。
可是要完成該“入隊”操作,我們必須對當前兩個棧的狀態進行判斷,因為兩個棧的存儲狀態會影響到元素的排列順序與輸出順序。大致可以將兩個棧的存儲狀態分為三類:
-
s1滿,s2空:將s1中的元素依次出棧,在依次入棧s2。此時,s1空,在將需要“入隊”的元素入棧s1,便可以得到“先進先出”順序的元素序列
-
s1不滿,s2空:同樣將s1存有的元素依次次出棧,在依次入棧s2,這樣的做法可以保證s1中已經存儲的元素,可以在s2中按正確的順序排列,並且不會影響到新“入隊”的元素
-
s1滿,s2不空:此時無法進行入隊操作
從上面的分析情況可得,當s1中存在元素時,s2必須為空,否則無法執行“入隊”操作。
原因分析:當s2不空的時候,s2中的元素是按“先進先出”的順序進行排列的,此時若是將s1中的元素依次出棧,再依次入棧到s2中的話,會導致無法實現“先進先出”特點的輸出。例如:
我們想要輸出a b c d e f的隊列;
此時 s2中存儲的是 a b c ,其中a為棧頂 ,且符合不空的情況;
s1按 e d c 存儲,且e為棧頂,且符合不滿的情況;
則此時對s1依次出棧,再依次出棧至s2的操作後;
s2的存儲情況變更為: d e f a b c 如下圖所示:
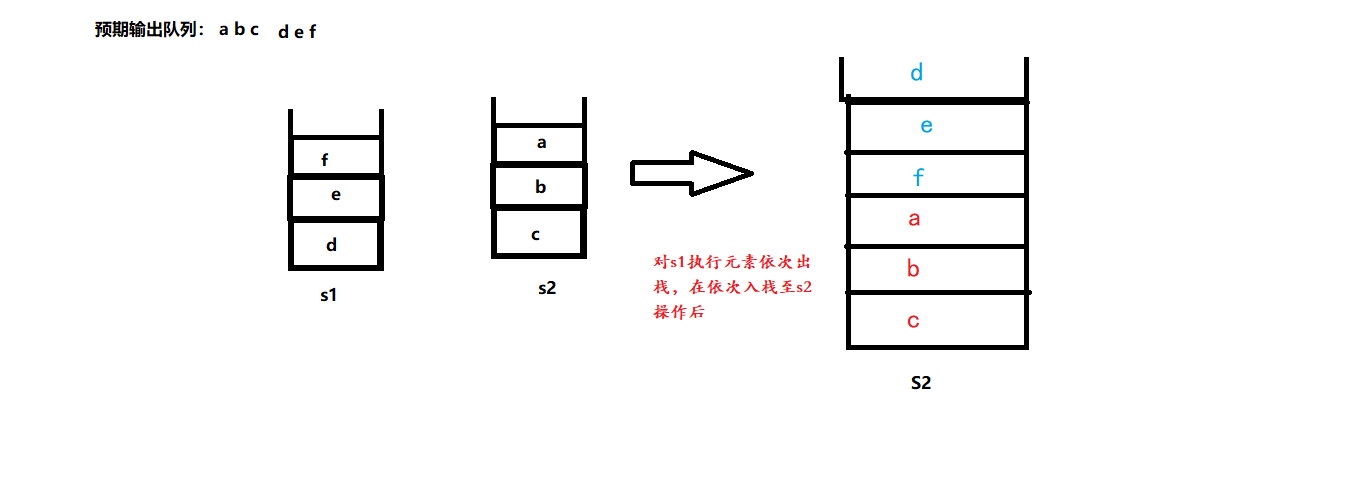
此時我們可以看出,s1中的元素排列順序是正確的,s2中原本的元素排列順序也是正確的。但是,此時對s2執行“出隊”的操作後,我們得到的隊列就是錯的。所以我們需要再執行“入隊”的操作前,保證s2是為空的狀態
代碼實現:
- “入隊”演算法
//入隊
bool enQueue(s1,s2,int x)
{
int temp; //用於存儲出棧的元素的值
//1.判斷棧s1是否已滿,此時分為兩種情況(滿了 or 未滿)
if (s1->top + 1 >= maxSize)
{
//說明棧s1已滿,此時分為兩種情況(棧s2空 or 棧s2不空)
if ( isEmpty(s2) )
{
//此時棧s2為空,所以需要把棧s1的元素依次出棧到s2中
while( ! isEmpty(s1) )
{
pop(s1,&temp); //把出棧元素暫時存儲在temp中
push(s2,temp); //把變數temp中的元素入棧到s2
}
push(s1,x); //此時棧s1為空,所以可以把元素x入棧到s1
return true;
}
else
{
//此時棧s2不空,所以無法入隊
return false;
}
}
else
{
//此時棧s1未滿,所以可以把元素x入棧到s1中
push(s1,x);
}
return true;
}
- "出隊"演算法
//出隊
bool enQueue(s1,s2,&x)
{
int temp; //為了存儲出棧的元素
//1.判斷隊列是否為空,此時分為兩種情況(空 or 不空)
if (isQueueEmpty(s1,s2))
{
return false;
}
else
{
//說明隊列不空,此時又分為兩種情況(棧s2空 or 棧s2不空)
if ( !isEmpty(s2) )
{
//說明棧s2不空,則直接把元素出棧
pop(s2,&x);
}
else
{
//說明棧s2為空,此時需要把棧s1的元素依次出棧到s2中
while( ! isEmpty(s1) )
{
pop(s1,&temp); //把出棧元素暫時存儲在temp中
push(s2,temp); //把變數temp中的元素入棧到s2
}
pop(s2,&x);
}
}
return true;
}
- "判斷隊列為空"演算法
//判斷隊列為空
int isQueueEmpty(s1,s2)
{
if (isEmpty(s1) && isEmpty(s2))
{
return 1;
}
else
return 0;
}



