引言 關係資料庫中的關係滿足一定要求的,滿足不同程度要求的為不同的範式,共有6種範式。 滿足最低要求的叫第一範式,簡稱 1NF;在第一範式的基礎上滿足進一步要求的稱為第二範式,簡稱 2NF; 其餘範式以此類推。 對於各種範式之間有如下關係: 5NF ∈ 4NF ∈ BCNF ∈ 3NF ∈ 2NF ...
引言
關係資料庫中的關係滿足一定要求的,滿足不同程度要求的為不同的範式,共有6種範式。
滿足最低要求的叫第一範式,簡稱 1NF;在第一範式的基礎上滿足進一步要求的稱為第二範式,簡稱 2NF; 其餘範式以此類推。
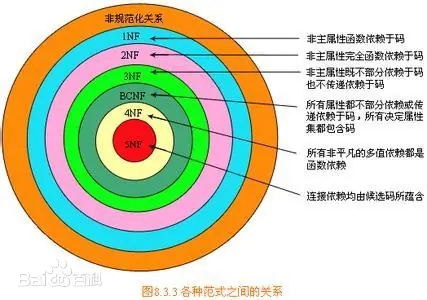
對於各種範式之間有如下關係:
5NF ∈ 4NF ∈ BCNF ∈ 3NF ∈ 2NF ∈ 1NF
第一範式 1NF
- 定義: 屬於第一範式關係的所有屬性都不可再分,即數據項不可分。
- 理解: 第一範式強調數據表的原子性,是其他範式的基礎。如下圖所示資料庫就不符合第一範式:
| 公司名稱 | 地址 | 電話 | ||
| 名稱 | 數量 | |||
| 公司名稱 | 地址 | 商品名稱 | 商品數量 | 電話 |
|---|
上表就符合第一範式關係。
但日常生活中僅用第一範式來規範表格是遠遠不夠的,依然會存在數據冗餘過大、刪除異常、插入異常、修改異常的問題,此時就需要引入規範化概念,將其轉化為更標準化的表格,減少數據依賴。
- 規範化: 一個低一級的關係模式通過模式分解可以轉化為若幹個高一級範式的關係模式的集合,這個過程叫做規範化。
第二範式 2NF
- 定義: 若某關係 R 屬於第一範式,且每一個非主屬性完全函數依賴於任何一個候選碼,則關係 R 屬於第二範式。
此處我們需要理解非主屬性、候選碼和完全函數依賴的概念。 - 候選碼: 若關係中的某一屬性組的值能唯一地標識一個元組,而其子集不能,則稱該屬性組為候選碼。若一個關係中有多個候選碼,則選定其中一個為主碼。
以下所有內容中,主碼或候選碼都簡稱為碼。
例如
下圖所示的學生表中,學號和姓名都可以唯一標識一個元組,故該表的候選碼為學號和姓名,主碼我們可以隨便選定其中一個,則選學號為主碼。
| 學號 | 姓名 | 年齡 | 性別 |
|---|---|---|---|
| 101 | 劉晨 | 19 | 女 |
| 102 | 王琪 | 21 | 男 |
| 103 | 張宇 | 20 | 男 |
| 104 | 李琛 | 19 | 女 |
| 105 | 歐陽慧 | 20 | 女 |
- 主屬性: 所有候選碼的屬性稱為主屬性。不包含在任何候選碼中的屬性稱為非主屬性或非碼屬性。
在上面的學生表中,學號和姓名就是該關係的主屬性,年齡和性別就是非主屬性。
- 函數依賴: 設 R (U) 是屬性集 U 上的關係模式,X、Y 是 U 的子集。若對於 R (U) 的任意一個可能的關係 r,r 中不可能存在兩個元組在 X 上的屬性值相等,而在 Y 上的屬性值不等,則稱 Y 函數依賴於 X 或 X 函數確定 Y。
- 完全函數依賴: 設 R (U) 是屬性集 U 上的關係模式,X、Y 是 U 的子集。如果 Y 函數依賴於 X,且對於 X 的任何一個真子集 X’,都有 Y 不函數依賴於 X’,則稱 Y 對 X 完全函數依賴。記作:如果 Y 函數依賴於 X,但 Y 不完全函數依賴於 X,則稱 Y 對 X 部分函數依賴。
X ---> Y Y 函數依賴於 X
X -F-> Y Y 函數完全依賴於 X
X -P-> Y Y 函數部分依賴於 X
- 理解: 第二範式是指每個表必須有一個(有且僅有一個)數據項作為關鍵字或主鍵(primary key),其他數據項與關鍵字或者主鍵一一對應,即其他數據項完全依賴於關鍵字或主鍵。由此可知單主屬性的關係均屬於第二範式。
判斷一個關係是否屬於第二範式:
- 找出數據表中的所有碼;
- 找出所有主屬性和非主屬性;
- 判斷所有的非主屬性對碼的部分函數依賴。
以上面的學生表為例,表中的碼為學號(碼可以為學號或者姓名,此處假定碼為學號),非主屬性為性別、年齡(其餘都為主屬性),當學號確定時,性別、年齡也都惟一的被確定為,故學生表的設計滿足第二範式(學生表為單主屬性的關係)。
例如
下麵舉一個不滿足第二範式的關係。
有關係模式 S-L-C (Sno, Sdept, Sloc, Cno, Grade),其中 Sno, Sdept, Sloc, Cno, Grade 依次表示學生的學號、所在的系、住處、課程號、班級,並且每個系的學生住在同一個地方。可知 S-L-C 的碼為(Sno, Cno),則存在以下函數依賴:
(Sno, Cno) -F-> Ggrade
Sno ---> Sdept , (Sno, Cno) -P-> Sdept
Sno ---> Sloc , (Sno, Cno) -P-> Sloc , Sdept ---> Sloc (每個系的學生住在同一個地方)
可以看到,非主屬性 Sloc、Sdept 並不完全函數依賴於碼,因此關係模式 S-L-C (Sno, Sdept, Sloc, Cno, Grade) 不符合第二範式。
第三範式 3NF
- 定義: 非主屬性既不傳遞依賴於碼,也不部分依賴於碼。
首先我們要理解傳遞函數依賴的概念。
在R(U)中,若X-->Y,Y-/->X,Y-->Z,Z不屬於Y,則稱Z對X傳遞函數依賴。記作 X -傳遞-> Z。
- 理解: 第三範式要求在滿足第二範式的基礎上,任何非主屬性不依賴於其他非主屬性,即在第二範式的基礎上,消除了傳遞依賴。
在下圖 S-L 關係中,Sloc 對 Sno 傳遞函數依賴,故該關係不屬於第三範式。
graph LR A(Sno) --> B(Sdept) B --> C(Sloc) A --> CBC範式 BCFN
- 定義: 關係模式 R 中,若每一個決定因素都包含碼,則 R 屬於 BCFN。
- 理解: 根據定義我們可以得到結論,一個滿足 BC 範式的關係模式有:
- 所有非主屬性對每一個碼都是完全函數依賴;
- 所有主屬性對每一個不包含它的碼也是完全函數依賴;
- 沒有任何屬性完全函數依賴於非碼的任何一組屬性。
例如有關係模式 C (Cno, Cname, Pcno),Cno, Cname, Pcno 依次表示課程號、課程名、先修課。可知關係 C 只有一個碼 Cno,且沒有任何屬性對 Cno 部分函數依賴或傳遞函數依賴,所以關係 C 屬於第三範式,同時 Cno 是 C 中的唯一決定因素,所以 C 也屬於 BC 範式。
第四範式 4NF
- 定義: 限制關係模式的屬性之間不允許有非平凡且非函數依賴的多值依賴。
- 理解: 顯然一個關係模式是 4NF,則必為 BCNF。也就是說,當一個表中的非主屬性互相獨立時(3NF),這些非主屬性不應該有多值,若有多值就違反了 4NF。
第五範式 5NF
第五範式有以下要求:
- 必須滿足第四範式;
- 表必須可以分解為較小的表,除非那些表在邏輯上擁有與原始表相同的主鍵。
第五範式是在第四範式的基礎上做的進一步規範化。第四範式處理的是相互獨立的多值情況,而第五範式則處理相互依賴的多值情況。



