用python計算圓周率PI

‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬描述

用python計算圓周率PI‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬

‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬1.要求能算到小數點後面越多越好（5分）‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬

‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬2.並用進度條提示算的進度，能給出多種進度條越好（5分）‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬

‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪3.要求給出算圓周率Pi具體公式或者演算法說明

一、具體公式：

萊布尼茨公式

π/4=1-1/3+1/5-1/7+1/9-1/11+……

蒙特卡羅法（打鳥法）

一個正方形內部相切一個圓，圓和正方形的面積之比是π/4。 
在這個正方形內部，隨機產生n個點（這些點服從均勻分佈），計算它們與中心點的距離是否大於圓的半徑，以此判斷是否落在圓的內部。

統計圓內的點數，與n的比值乘以4，就是π的值。理論上，n越大，計算的π值越準。

二、代碼如下：

（1）、蒙特卡羅法（打鳥法）

import math
import time
scale=10
print("執行開始")
t=time.process_time()
for i in range(scale+1):
    a,b='**'*i,'..'*(scale-i)
    c=(i/scale)*100
    π=4*(4*math.atan(1/5)-math.atan(1/239))
    print("[{:3}{}->{}%]".format(a,b,c))
    time.sleep(0.1)
print("π =",format(π))
print("運行時間：{:.2f}s".format(t))
print("執行結束")

運行結果如下：

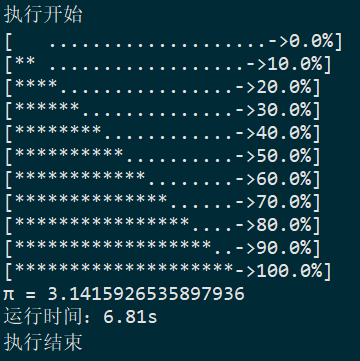
（2）、萊布尼茲公式

import time
import math
total,s,n,t=0.0,1,1.0,1.0
while(math.fabs(t)>=1e-6):
    total+=t
    n+=2
    s=-s
    t=s/n
k=total*4
scale=50
print("".center(scale//2,"-"))
start = time.perf_counter()
for i in range(scale+1):
    a="*"*i
    b="."*(scale-i)
    c=(i/scale)*100
    d=time.perf_counter() - start
    print("\r{:^3.0f}%[{}->{}]{:.2f}s".format(c,a,b,d),end='')
    time.sleep(0.1)
print("\n π值是{:.10f}".format(k))

運行結果如下：

（3）、萊布尼茲公式

import time
import math
  
  
class Index(object):
    def __init__(self, number=50, decimal=2):
        self.decimal = decimal
        self.number = number
        self.a = 100/number  
  
    def __call__(self, now, total):
        percentage = self.percentage_number(now, total)
        well_num = int(percentage / self.a)
        progress_bar_num = self.progress_bar(well_num)
        result = "\r%s %s" % (progress_bar_num, percentage)
        return result
  
    def percentage_number(self, now, total):
        return round(now / total * 100, self.decimal)
  
    def progress_bar(self, num):
        well_num = "#" * num
        space_num = " " * (self.number - num)
        return '[%s%s]' % (well_num, space_num)
  
  
  
index = Index()
 
 
total,s,n,t=0.0,1,1.0,1.0
while(math.fabs(t)>=1e-6):
    total+=t
    n+=2
    s=-s
    t=s/n
k=total*4
  
start = 371
for i in range(start + 1):
    print(index(i, start), end='')
    time.sleep(0.01)
     
     
print("\n π值是{:.10f}".format(k))

運行結果如下：