【前端動畫】—— 再看tweenJS

16開始接觸前端，一直對一個問題特別感興趣，那就是js動畫，也就是從那時起開始探究動畫的各種表現形式，也是那個時候開始意識到編程這塊東西最終考驗的就是抽象和邏輯，而這一切完全是數學裡邊的東西。

最早接觸tweenJS是去年還是前年來著有點忘了，不過當時有點不大看得懂，勉勉強強算是過了一遍，不過有了這個體驗之後，我自己做了一套項目，裡邊有個返回頂部按鈕，當滑鼠按下時，我使用了sin函數控制陰影的大小，具體效果表現還著實驚艷了自己一番，就像呼吸燈那樣，於是在那以後的各種面試會上，我都樂此不彼的給面試官展示我的項目。現在想想覺得還是有趣極了。

有點扯遠了，現在來說說tweenJS，因為我很懶所以下麵會使用TT代表tweenJS。TT其實是一個非常小巧的動畫庫--體積小代碼又精煉，然而他所能實現的各種效果確實很多。那最簡單的線性運動來說，代碼如下

/*
 * @param { number } t （當前次數）    
 * @param { number } b beginning value（初始值）   
 * @param { number } c change in value（變化量）    
 * @param { number } d （動畫次數）
 */    
function(t, b, c, d) {    
    return c * t / d + b;    
}

先不說上面的代碼，我這裡想討論一下動畫，其實一個動畫就是起點到終點某個元素的某個屬性隨著時間逐漸改變的過程，無論這個屬性是距離，顏色，大小，everything，只要能隨時間改變，我們就可以稱之為動畫。現在再看上邊的代碼，為了便於討論方便b也就是動畫的起點我們可以設置為0，所以現在我們以距離為例討論一下這個函數。b為0，那麼決定最終位置的就是c，d(是持續時間),t。大家可以想想初中我們學到的公式：路程 / 時間 = 速度，所以在上邊的公式里，c/d 是一個常量，而唯一變化的時間t,配合速度相乘，就是確定在某一個時間點上該物體應該所在的位置，而隨著時間逐漸改變t之後，就會產生一個動畫，舉例如下：

實例

<style>
.example{
  width:120px;
  height:20px;
  background:#000;
}
</style>
<div id="test" class="example"></div>
<script>
    function linear(t, b, c, d) {    
        return c * t / d + b;    
    } 
    //我們在這裡要讓div#test向下移動一100px,持續時間是2s，這裡註意一下間隔的
    //演算法，總共需要運行10次才能到達100px 的位置，所以間隔的演算法為 2000 / 10 = 200ms/次，
    // 塊級作用域里，t從 0 - 10 ，每一次for迴圈啟動一個定時器，分別從0，200，400，600，2000後設置marginTop的值
    for( let t = 0;t <=10;t++ )
        setTimeout(
            function(){
                test.style.marginTop = linear( t,0,100,10 ) + 'px'
            },
            200*t
        )
        
</script>

運行實例 »

在製作web動畫時，有一個要求是，60fps準則，那麼我們每次時間間隔因為 1000/ 60 ，這樣的話t 每次的變化量就可以寫成 t += 1000/60 ,其他條件不變，因此總共持續的次數就是 2000 / （1000/60），代碼可以寫成這樣：

function linear(t, b, c, d) {            
    return c * t / d + b;        
}     
  
for( let t = 0;t <=2000;t += (1000/60) )        
    setTimeout(            
        function(){                
            let curT = Math.floor(t/(1000/60));             
            test.style.marginTop = linear( curT,0,100,2000/(1000/60) ) + 'px'            
         },            
         t        
     )

運行實例

當然啦，現在推薦requestAnimationFrame這個window的api，所以儘量用這個，當然基本演算法還是差不多的。

再來看一個Sine.easeIn:

/*
 * @param { number } t （當前次數）    
 * @param { number } b beginning value（初始值）   
 * @param { number } c change in value（變化量）    
 * @param { number } d （動畫次數）
 */  
function SinEaseIn(t, b, c, d) {    
    return -c * Math.cos(t/d * (Math.PI/2)) + c + b;    
}

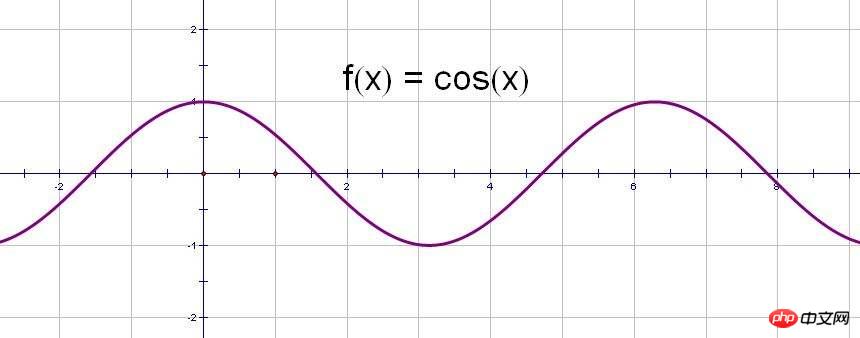
仍以距離為例，b我們也設置為0，更方便弄懂，cos函數在 0 -- (t/d)*0.5π上的變化範圍為 1 -- cos((t/d)*0.5π)，t/d <=1,

即 為 1 -- cos(0.5π)  => 1 -- 0 所以，正好是cos函數的四分之一個周期，我下麵找個圖，看著更清晰：

所以SinEaseIn 函數的返回值會從 0 - c變化 ，最後到達最終位置。