Java實現常見查找演算法 查找是在大量的信息中尋找一個特定的信息元素,在電腦應用中,查找是常用的基本運算,例如編譯程式中符號表的查找。 線性查找 線性查找(Linear Search)是一種簡單的查找演算法,用於在數據集中逐一比較每個元素,直到找到目標元素或搜索完整個數據集。它適用於任何類型的數據集 ...
Java實現常見查找演算法
查找是在大量的信息中尋找一個特定的信息元素,在電腦應用中,查找是常用的基本運算,例如編譯程式中符號表的查找。
線性查找
線性查找(Linear Search)是一種簡單的查找演算法,用於在數據集中逐一比較每個元素,直到找到目標元素或搜索完整個數據集。它適用於任何類型的數據集,無論是否有序,但在大型數據集上效率較低,因為它的時間複雜度是 O(n),其中 n 是數據集的大小。
以下是線性查找的基本步驟:
- 從數據集的第一個元素開始,逐一遍歷每個元素。
- 比較當前元素與目標元素是否相等。
- 如果相等,表示找到了目標元素,返回當前元素的索引位置。
- 如果不相等,繼續遍歷下一個元素。
- 如果遍歷完整個數據集都沒有找到目標元素,則返回一個表示元素不存在的標識(如 -1)。
以下是使用Java實現線性查找的示例代碼:
public class LinearSearch {
public static int linearSearch(int[] arr, int target) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == target) {
return i; // 目標元素的索引位置
}
}
return -1; // 目標元素不存在於數組中
}
public static void main(String[] args) {
int[] arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int target = 23;
int result = linearSearch(arr, target);
if (result == -1) {
System.out.println("目標元素不存在於數組中");
} else {
System.out.println("目標元素的索引位置為: " + result);
}
}
}
二分查找
二分查找演算法(Binary Search)是一種高效的查找演算法,用於在有序數組或列表中查找特定元素的位置。它的基本思想是通過將數組分成兩半,然後確定目標元素在哪一半,然後繼續在那一半中搜索,重覆這個過程直到找到目標元素或確定不存在。
二分查找演算法的時間複雜度是 O(log n),其中 n 是數據集的大小。這使得它在大型有序數據集中的查找操作非常高效,每次將數據集分成兩半,然後確定目標元素在哪一半,然後繼續在那一半中搜索。每次操作都將數據集的規模減少一半,因此它的時間複雜度是對數級別的.
需要註意的是,二分查找演算法要求數據集必須是有序的。如果數據集無序,需要先進行排序操作。排序操作通常具有較高的時間複雜度(如快速排序的平均時間複雜度為 O(n log n)),因此總體上二分查找演算法加上排序操作的時間複雜度可能會更高。
總結起來,二分查找演算法是一種高效且常用的查找演算法,在大型有序數據集中具有較低的時間複雜度。
以下是二分查找演算法的詳細步驟:
- 初始化左指針
left為數組的起始位置,右指針right為數組的結束位置。 - 計算中間位置
mid,即mid = left + (right - left) / 2。 - 比較中間位置的元素與目標元素:
- 如果中間位置的元素等於目標元素,則返回中間位置。
- 如果中間位置的元素大於目標元素,則更新右指針
right = mid - 1,並回到步驟2。- 如果中間位置的元素小於目標元素,則更新左指針
left = mid + 1,並回到步驟2。
- 如果中間位置的元素小於目標元素,則更新左指針
- 如果左指針大於右指針,則表示目標元素不存在於數組中。
以下是使用Java實現二分查找演算法的示例代碼(迭代法):
public class BinarySearch {
public static int binarySearch(int[] arr, int target) {
int left = 0;// 左指針,初始為數組起始位置
int right = arr.length - 1;// 右指針,初始為數組結束位置
while (left <= right) {
int mid = left + (right - left) / 2; // 計算中間位置
if (arr[mid] == target) { // 如果中間位置的元素等於目標元素,則找到目標元素
return mid;
} else if (arr[mid] < target) { // 如果中間位置的元素小於目標元素,則在右半部分繼續查找
left = mid + 1;
} else { // 如果中間位置的元素大於目標元素,則在左半部分繼續查找
right = mid - 1;
}
}
return -1; // 目標元素不存在於數組中
遞歸法
public class BinarySearchRecursive {
public static int binarySearch(int[] arr, int target, int left, int right) {
if (left <= right) {
int mid = left + (right - left) / 2;// 計算中間位置
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {// 如果中間位置的元素小於目標元素,則在右半部分繼續查找
return binarySearch(arr, target, mid + 1, right);
} else {// 如果中間位置的元素大於目標元素,則在左半部分繼續查找
return binarySearch(arr, target, left, mid - 1);
}
}
return -1; // 目標元素不存在於數組中
}
public static void main(String[] args) {
int[] arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int target = 23;
int result = binarySearch(arr, target, 0, arr.length - 1);
if (result == -1) {
System.out.println("目標元素不存在於數組中");
} else {
System.out.println("目標元素的索引位置為: " + result);
}
}
}
如果數組中有多個相同的目標元素,上面的演算法只會返回其中一個的索引位置,可以優化一下返回全部元素的下標
// 迭代
public static List<Integer> binarySearchAllIterative(int[] arr, int target) {
List<Integer> indices = new ArrayList<>();
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
indices.add(mid);
// 向左掃描找到所有相同元素的索引
int temp = mid - 1;
while (temp >= 0 && arr[temp] == target) {
indices.add(temp);
temp--;
}
// 向右掃描找到所有相同元素的索引
temp = mid + 1;
while (temp < arr.length && arr[temp] == target) {
indices.add(temp);
temp++;
}
break; // 結束迴圈,避免重覆掃描
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return indices;
}
// 遞歸
public class BinarySearchMultiple {
public static List<Integer> binarySearchAll(int[] arr, int target) {
List<Integer> indices = new ArrayList<>();
binarySearchAllRecursive(arr, target, 0, arr.length - 1, indices);
return indices;
}
public static void binarySearchAllRecursive(int[] arr, int target, int left, int right, List<Integer> indices) {
if (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
indices.add(mid); // 將找到的索引加入列表
// 繼續在左半部分和右半部分繼續查找相同目標元素的索引
binarySearchAllRecursive(arr, target, left, mid - 1, indices);
binarySearchAllRecursive(arr, target, mid + 1, right, indices);
} else if (arr[mid] < target) {
binarySearchAllRecursive(arr, target, mid + 1, right, indices);
} else {
binarySearchAllRecursive(arr, target, left, mid - 1, indices);
}
}
}
}
通常情況下,迭代法比遞歸法的效率要高。這是因為迭代法避免了函數調用的開銷,而函數調用涉及堆棧管理、參數傳遞等操作,會導致一定的性能損耗。此外,迭代法通常更容易優化,可以通過使用迴圈不斷更新變數的方式來進行計算,從而更有效地利用計算資源。
插值查找
插值查找演算法是一種基於有序數組的搜索演算法,類似於二分查找,但它在選擇比較的元素時使用了一種更為精細的估計方法,從而更接近目標元素的位置。插值查找的基本思想是根據目標元素的值與數組中元素的分佈情況,估算目標元素在數組中的大致位置,然後進行查找。
在二分查找中,mid的計算方式如下:
\[mid = \frac{low+high}{2} \]將low從分數中提取出來,mid的計算就變成了:
\[mid =low + \frac{low+high}{2} \]在插值查找中,mid的計算方式轉換成了:
\[mid =low + \frac{key-a[low] }{a[high] - a[low]}(high-low) \]low 表示左邊索引left, high表示右邊索引right,key 就是target
插值查找演算法的步驟如下:
- 初始化左指針
left為數組的起始位置,右指針right為數組的結束位置。 - 使用插值公式來估算目標元素的位置:
pos = left + ((target - arr[left]) * (right - left)) / (arr[right] - arr[left])
其中,target是目標元素的值,arr[left]和arr[right]分別是當前搜索範圍的左邊界和右邊界的元素值。 - 如果估算位置
pos對應的元素值等於目標元素target,則找到目標元素,返回位置pos。 - 如果估算位置
pos對應的元素值小於目標元素target,則說明目標元素在當前位置的右側,更新left = pos + 1。 - 如果估算位置
pos對應的元素值大於目標元素target,則說明目標元素在當前位置的左側,更新right = pos - 1。 - 重覆步驟 2 到步驟 5,直到找到目標元素或搜索範圍縮小到無法繼續搜索為止。
插值查找的優勢在於當數組元素分佈均勻且有序度較高時,其效率可以比二分查找更高。然而,當數組元素分佈不均勻或有序度較低時,插值查找可能會導致性能下降,甚至變得不如二分查找。
需要註意的是,插值查找演算法的時間複雜度通常為 O(log log n),但在某些特殊情況下,可能會退化為 O(n)。因此,在選擇搜索演算法時,需要根據具體的數據分佈情況和性能需求進行考慮。
插值查找演算法的示例代碼:
public class InterpolationSearch {
/**
* 插值查找演算法
*
* @param arr 有序數組
* @param target 目標元素
* @return 目標元素在數組中的索引位置,如果不存在則返回 -1
*/
public static int interpolationSearch(int[] arr, int target) {
int left = 0; // 左指針,初始為數組起始位置
int right = arr.length - 1; // 右指針,初始為數組結束位置
while (left <= right && target >= arr[left] && target <= arr[right]) {
// 使用插值公式估算目標元素的位置
int pos = left + ((target - arr[left]) * (right - left)) / (arr[right] - arr[left]);
if (arr[pos] == target) {
return pos; // 找到目標元素
}
if (arr[pos] < target) {
left = pos + 1; // 目標元素在右半部分
} else {
right = pos - 1; // 目標元素在左半部分
}
}
return -1; // 目標元素不存在於數組中
}
public static void main(String[] args) {
int[] arr = {2, 5, 8, 12, 16, 23, 38, 56, 72, 91};
int target = 23;
int result = interpolationSearch(arr, target);
if (result == -1) {
System.out.println("目標元素不存在於數組中");
} else {
System.out.println("目標元素的索引位置為: " + result);
}
}
}
斐波那契查找
斐波那契查找是一種基於黃金分割原理的查找演算法,它是對二分查找的一種改進。斐波那契查找利用了斐波那契數列的特性來確定查找範圍的分割點,從而提高了查找效率。
隨著斐波那契數列的遞增,前後兩個數的比值會越來越接近0.618,利用這個特性,我們就可以將黃金比例運用到查找技術中,斐波那契查找原理與前兩種相似,僅僅改變了中間結點(mid)的位置,mid不再是中間或插值得到,而是位於黃金分割點附近,即mid=low+F(k-1)-1(F代表斐波那契數列)
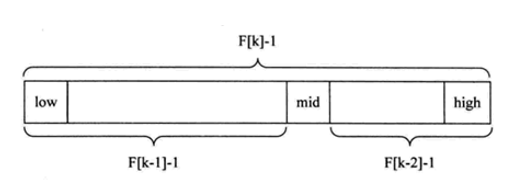
斐波那契查找的基本思想如下:
-
首先,需要準備一個斐波那契數列,該數列滿足
每個元素等於前兩個元素之和。例如:0, 1, 1, 2, 3, 5, 8, 13, ... -
初始化左指針
left和右指針right分別指向數組的起始位置和結束位置。 -
根據數組長度確定一個合適的斐波那契數列元素作為分割點
mid,使得mid儘可能接近數組長度。 -
比較目標元素與分割點mid
對應位置的元素值:
- 如果目標元素等於
arr[mid],則找到目標元素,返回位置mid。 - 如果目標元素小於
arr[mid],則說明目標元素在當前位置的左側,更新右指針為mid - 1。 - 如果目標元素大於
arr[mid],則說明目標元素在當前位置的右側,更新左指針為mid + 1。
- 如果目標元素等於
-
重覆步驟 3 和步驟 4,直到找到目標元素或搜索範圍縮小到無法繼續搜索為止。、
斐波那契查找的優勢在於它能夠更快地確定分割點,從而減少了比較次數。它的時間複雜度為 O(log n),與二分查找相同。然而,斐波那契查找需要預先計算斐波那契數列,並且在每次查找時都需要重新確定分割點,因此在實際應用中可能會帶來一定的額外開銷。
需要註意的是,斐波那契查找適用於有序數組,並且數組長度較大時效果更好。對於小規模的數組或者無序數組,二分查找可能更適合。
代碼示例:
public class FibonacciSearch {
public static int maxSize = 20;
public static void main(String[] args) {
int [] arr = {1,4, 10, 69, 1345, 6785};
System.out.println("index=" + fibSearch(arr, 1345));// 0
}
// 生成 斐波那契數列
public static int[] fib() {
int[] f = new int[20];
f[0] = 1;
f[1] = 1;
for (int i = 2; i < maxSize; i++) {
f[i] = f[i - 1] + f[i - 2];
}
return f;
}
/**
*
* @param a 數組
* @param key 我們需要查找的關鍵碼(值)
* @return 返回對應的下標,如果沒有-1
*/
public static int fibSearch(int[] a, int key) {
int low = 0;
int high = a.length - 1;
int k = 0; //表示斐波那契分割數值的下標
int mid = 0; //存放mid值
int f[] = fib(); //獲取到斐波那契數列
//獲取到斐波那契分割數值的下標
while(high > f[k] - 1) {
k++;
}
//因為 f[k] 值 可能大於 a 的 長度,因此我們需要使用Arrays類,構造一個新的數組,並指向temp[]
//不足的部分會使用0填充
int[] temp = Arrays.copyOf(a, f[k]);
//實際上需求使用a數組最後的數填充 temp
for(int i = high + 1; i < temp.length; i++) {
temp[i] = a[high];
}
while (low <= high) { // 只要這個條件滿足,就可以找
mid = low + f[k - 1] - 1;
if(key < temp[mid]) { //我們應該繼續向數組的前面查找(左邊)
high = mid - 1;
//說明
//1. 全部元素 = 前面的元素 + 後邊元素
//2. f[k] = f[k-1] + f[k-2]
//因為 前面有 f[k-1]個元素,所以可以繼續拆分 f[k-1] = f[k-2] + f[k-3]
//即 在 f[k-1] 的前面繼續查找 k--
//即下次迴圈 mid = f[k-1-1]-1
k--;
} else if ( key > temp[mid]) { // 我們應該繼續向數組的後面查找(右邊)
low = mid + 1;
//1. 全部元素 = 前面的元素 + 後邊元素
//2. f[k] = f[k-1] + f[k-2]
//3. 因為後面我們有f[k-2] 所以可以繼續拆分 f[k-1] = f[k-3] + f[k-4]
//4. 即在f[k-2] 的前面進行查找 k -=2
//5. 即下次迴圈 mid = f[k - 1 - 2] - 1
k -= 2;
} else { //找到
//需要確定,返回的是哪個下標
if(mid <= high) {
return mid;
} else {
return high;
}
}
}
return -1;
}
}
哈希查找
哈希查找演算法(Hashing)是一種用於高效查找數據的演算法,它將數據存儲在散列表(Hash Table)中,並利用散列函數將數據的關鍵字映射到表中的位置。哈希查找的核心思想是通過散列函數將關鍵字轉換為表中的索引,從而實現快速的查找操作。
在平均情況下,哈希查找的時間複雜度可以達到O(1)。但是,在最壞情況下,哈希查找的時間複雜度可能會退化到O(n),其中n是散列表中存儲的鍵值對數量
Java提供了用於實現哈希表(散列表)的數據結構,這就是HashMap類。HashMap是Java標準庫中最常用的哈希表實現之一,用於存儲鍵值對,並提供了快速的查找、插入和刪除操作。
通過leetcode第一題兩數之和可以瞭解哈希表的使用
代碼示例
public static int[] twoSum(int[] nums, int target) {
int[] indexs = new int[2];
HashMap<Integer, Integer> hashMap = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
if (hashMap.containsKey(nums[i])){
indexs[0] = i;
indexs[1] = hashMap.get(nums[i]);
return indexs;
}
hashMap.put(target - nums[i],i);
}
return indexs;
}
二叉樹查找
二叉搜索樹是一種特殊的二叉樹,它是一種有序的樹結構,可以用於實現二叉樹查找。在二叉搜索樹中,對於每個節點,其左子樹的值都小於該節點的值,而右子樹的值都大於該節點的值。這種結構使得在二叉搜索樹中可以快速地進行查找操作。
詳細看這篇文章 二叉搜索樹



