數據來源:House Prices - Advanced Regression Techniques 參考文獻: Comprehensive data exploration with Python 1. 導入數據 import pandas as pd import warnings warnin ...
數據來源:House Prices - Advanced Regression Techniques
參考文獻:
1. 導入數據
import pandas as pd
import warnings
warnings.filterwarnings('ignore') # 忽略警告
df_train = pd.read_csv('./house-prices-advanced-regression-techniques/train.csv')
df_train.columns
Index(['Id', 'MSSubClass', 'MSZoning', 'LotFrontage', 'LotArea', 'Street',
'Alley', 'LotShape', 'LandContour', 'Utilities', 'LotConfig',
'LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType',
'HouseStyle', 'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd',
'RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType',
'MasVnrArea', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual',
'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinSF1',
'BsmtFinType2', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', 'Heating',
'HeatingQC', 'CentralAir', 'Electrical', '1stFlrSF', '2ndFlrSF',
'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath',
'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'KitchenQual',
'TotRmsAbvGrd', 'Functional', 'Fireplaces', 'FireplaceQu', 'GarageType',
'GarageYrBlt', 'GarageFinish', 'GarageCars', 'GarageArea', 'GarageQual',
'GarageCond', 'PavedDrive', 'WoodDeckSF', 'OpenPorchSF',
'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'PoolQC',
'Fence', 'MiscFeature', 'MiscVal', 'MoSold', 'YrSold', 'SaleType',
'SaleCondition', 'SalePrice'],
dtype='object')
df_train['SalePrice'].describe()
count 1460.000000
mean 180921.195890
std 79442.502883
min 34900.000000
25% 129975.000000
50% 163000.000000
75% 214000.000000
max 755000.000000
Name: SalePrice, dtype: float64
2. 變數分析
import seaborn as sns
# 繪製售價的直方圖
sns.distplot(df_train['SalePrice']);
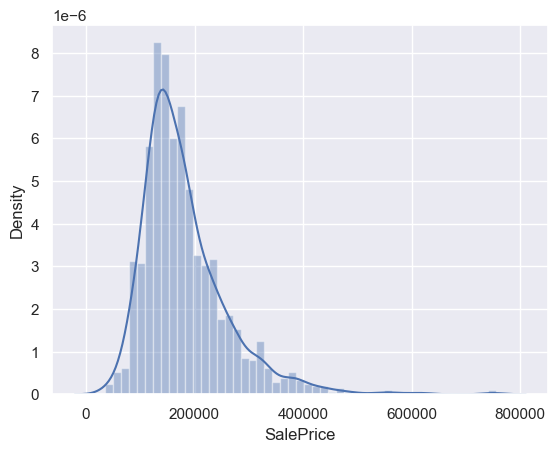
# 輸出偏度和峰度
print("Skewness: %f" % df_train['SalePrice'].skew())
print("Kurtosis: %f" % df_train['SalePrice'].kurt())
Skewness: 1.882876
Kurtosis: 6.536282
- 偏度(Skewness)是一種衡量隨機變數概率分佈的偏斜方向和程度的度量,是統計數據分佈非對稱程度的數字特征。偏度可以用來反映數據分佈相對於對稱分佈的偏斜程度。偏度的取值範圍為 (−∞,+∞),完全服從正態分佈的數據的偏度值為0,偏度值越大,表示數據分佈的右側尾部較長和較厚,稱為右偏態或正偏態;偏度值越小,表示數據分佈的左側尾部較長和較厚,稱為左偏態或負偏態。
- 峰度(Kurtosis)是一種衡量隨機變數概率分佈的峰態的指標。峰度高就意味著方差增大是由低頻度的大於或小於平均值的極端差值引起的。峰度可以用來度量數據分佈的平坦度(flatness),即數據取值分佈形態陡緩程度的統計量。
# 繪製GrLivArea(生活面積)的散點圖
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000));
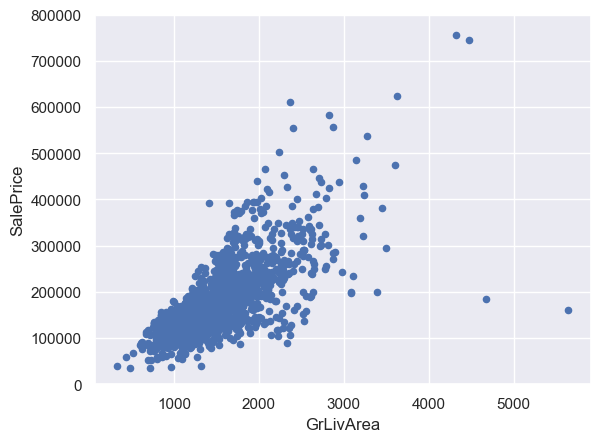
# 繪製TotalBsmtSF(地下室面積)的散點圖
var = 'TotalBsmtSF'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000));
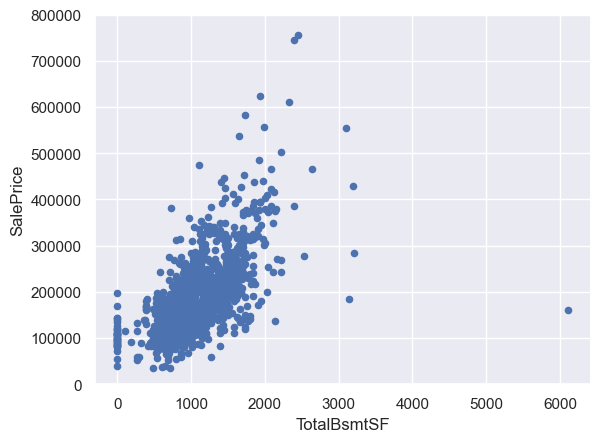
import matplotlib.pyplot as plt
# 繪製OverallQual(房屋整體材料和裝修質量)的箱線圖
var = 'OverallQual'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y='SalePrice', data=data)
fig.axis(ymin=0, ymax=800000);
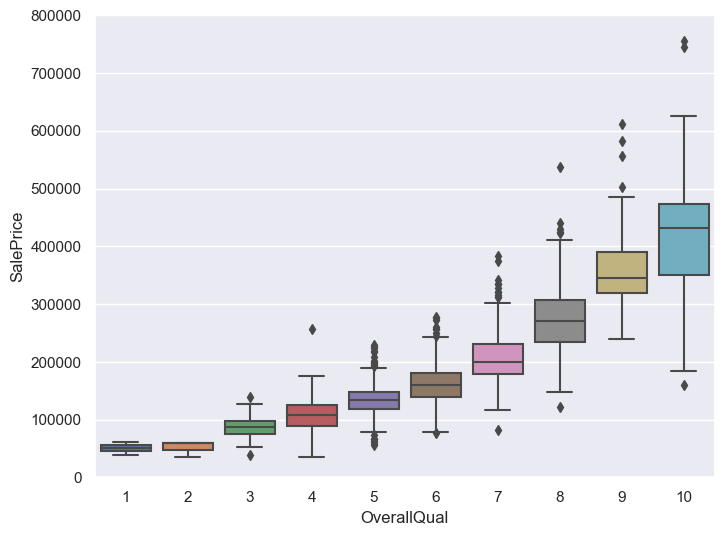
# 繪製YearBuilt(建造年份)的箱線圖
var = 'YearBuilt'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y='SalePrice', data=data)
fig.axis(ymin=0, ymax=800000)
plt.xticks(rotation=90); # 旋轉x軸標簽90度
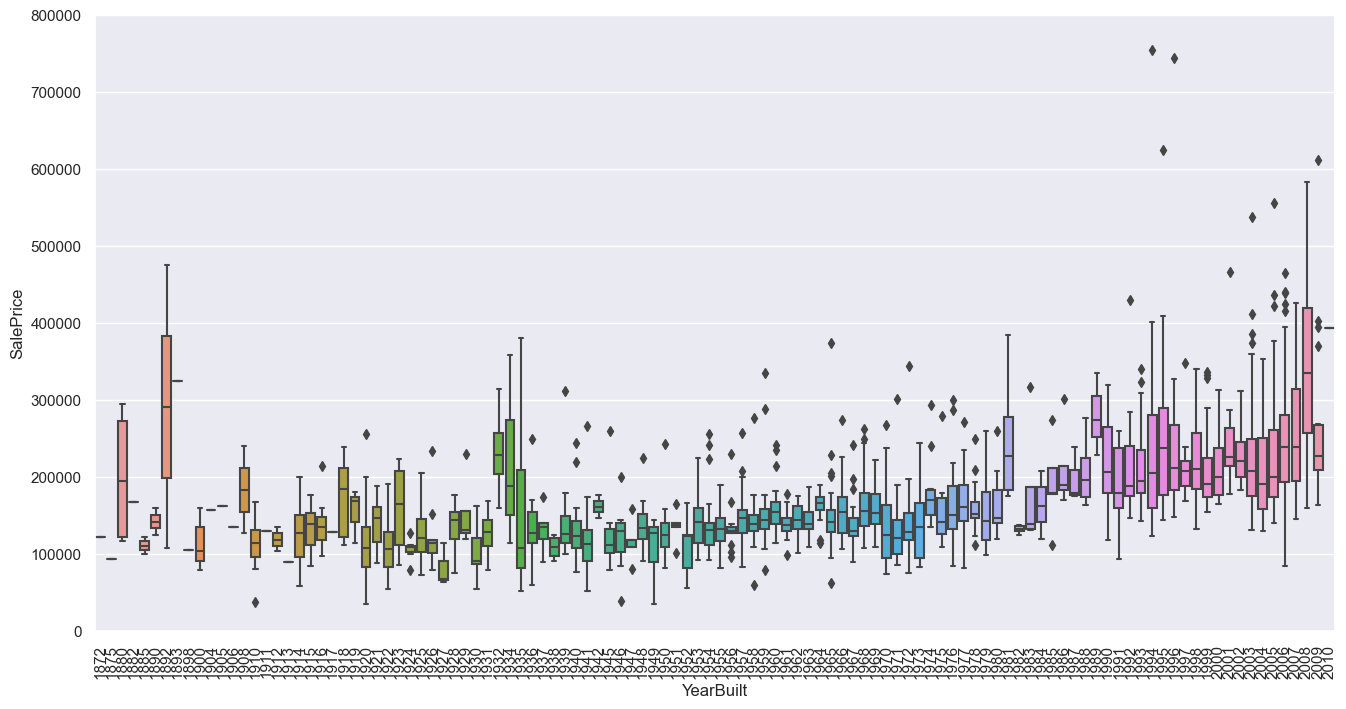
GrLivArea和TotalBsmtSF與SalePrice呈線性關係。TotalBsmtSF的斜率更大,說明地下室面積對售價的影響更大。OverallQual和YearBuilt與SalePrice呈正相關關係。
3. 更近進一步的變數分析
第二步只是憑著直覺對數據進行了初步的分析,下麵我們將對數據進行更進一步的分析。
# 繪製變數相關矩陣
corrmat = df_train.corr(numeric_only=True) # 僅對數值型變數進行相關分析
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);
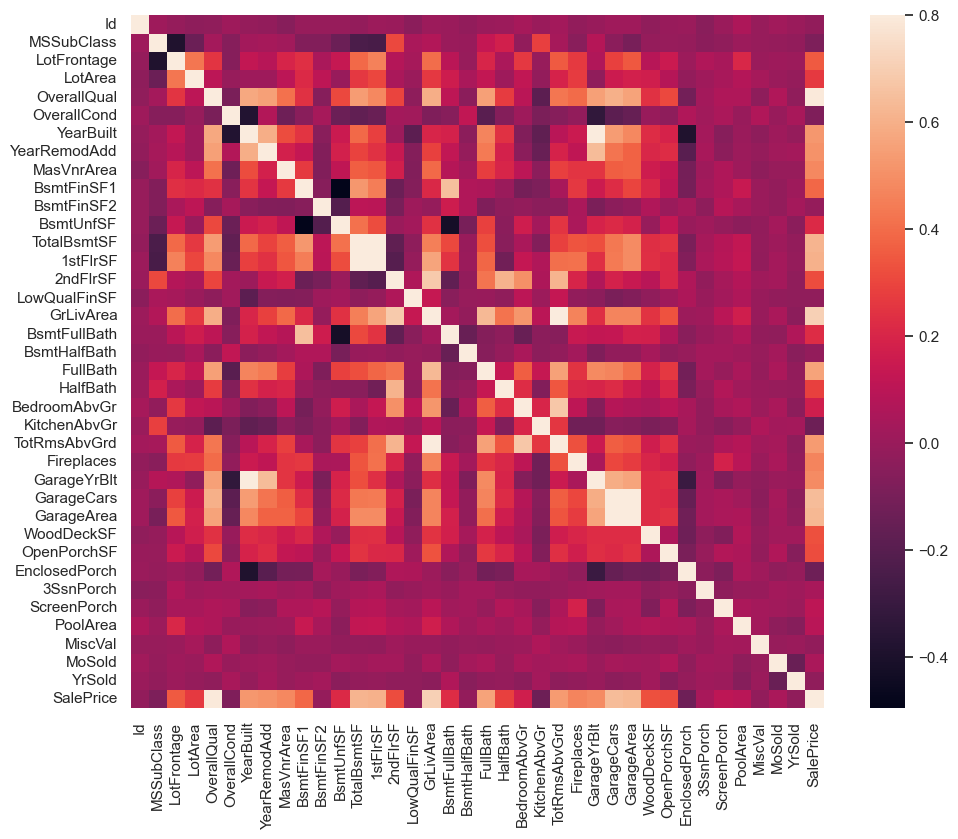
import numpy as np
# SalePrice與其他變數的相關係數
k = 10
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index # 與SalePrice相關係數最大的10個變數的索引
cm = np.corrcoef(df_train[cols].values.T) # 計算相關係數矩陣
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, annot=True, fmt='.2f', annot_kws={'size': 10},
yticklabels=cols.values, xticklabels=cols.values) # 設置annot=True,顯示相關係數
plt.show()
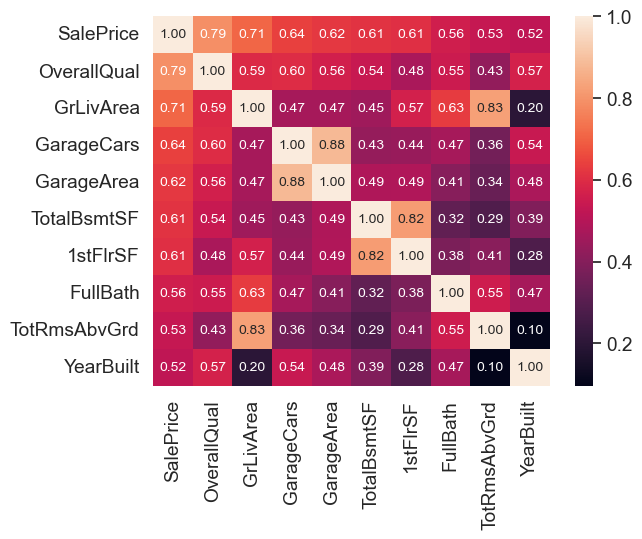
對於GarageCars和GarageArea,兩者有很強的關聯性,因此選擇保留GrageCars,因為它與SalePrice的相關性更高;TotalBsmtSF和1stFloor(First Floor square feet)也有很強的關聯性,地下室面積一般情況下不會大於一樓的面積,故選擇保留TotalBsmtSF。
因此最終保留了7個與SalePrice關聯最大的7個變數,分別是OverallQual、GrLivArea、GarageCars、TotalBsmtSF、FullBath、YearBuilt和YearRemodAdd。
# 繪製變數之間的pairplot散點圖
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF',
'FullBath', 'YearBuilt', 'YearRemodAdd']
sns.pairplot(df_train[cols], size=2.5)
plt.show()
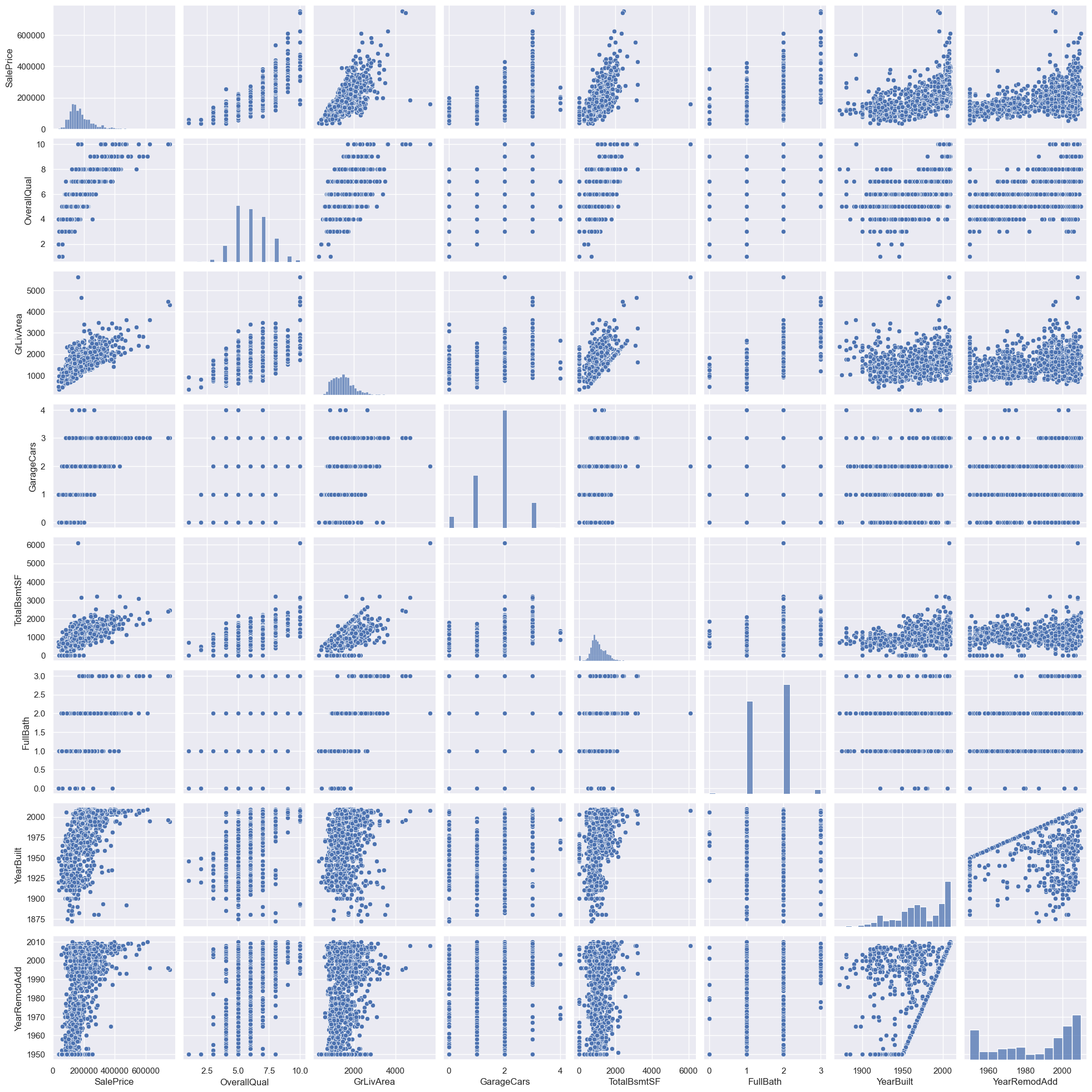
觀察成對散點圖:
TotalBsmtSF和GrLivArea兩者的圖像上有一條直線,仿佛邊界一般。說明地下室面積和生活面積成正比。就像上面提到的地下室面積和一樓面積的關係一樣。
SalePrice和YearBuilt的散點仿佛指數函數一般,說明房價隨著建造年份的增加而增加。
4. 缺失值處理
total = df_train.isnull().sum().sort_values(ascending=False) # 統計每個變數的缺失值個數
percent = (df_train.isnull().sum() / len(df_train)).sort_values(ascending=False) # 統計每個變數的缺失值比例
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)
| Total | Percent | |
|---|---|---|
| PoolQC | 1453 | 0.995205 |
| MiscFeature | 1406 | 0.963014 |
| Alley | 1369 | 0.937671 |
| Fence | 1179 | 0.807534 |
| MasVnrType | 872 | 0.597260 |
| FireplaceQu | 690 | 0.472603 |
| LotFrontage | 259 | 0.177397 |
| GarageYrBlt | 81 | 0.055479 |
| GarageCond | 81 | 0.055479 |
| GarageType | 81 | 0.055479 |
| GarageFinish | 81 | 0.055479 |
| GarageQual | 81 | 0.055479 |
| BsmtFinType2 | 38 | 0.026027 |
| BsmtExposure | 38 | 0.026027 |
| BsmtQual | 37 | 0.025342 |
| BsmtCond | 37 | 0.025342 |
| BsmtFinType1 | 37 | 0.025342 |
| MasVnrArea | 8 | 0.005479 |
| Electrical | 1 | 0.000685 |
| Id | 0 | 0.000000 |
df_train = df_train.drop((missing_data[missing_data['Total'] > 1]).index, axis=1) # 將缺失數量大於1的列刪去
df_train = df_train.drop(df_train.loc[df_train['Electrical'].isnull()].index) # 將Electrical缺失的行刪去
df_train.isnull().sum().max() # 檢查是否還有缺失值
0
from sklearn.preprocessing import StandardScaler
saleprice_scaled = StandardScaler().fit_transform(df_train['SalePrice'].to_numpy()[:, np.newaxis])
# 輸出異常值
low_range = saleprice_scaled[saleprice_scaled[:, 0].argsort()][:10]
high_range = saleprice_scaled[saleprice_scaled[:, 0].argsort()][-10:]
print('outer range (low) of the distribution:')
print(low_range)
print('\nouter range (high) of the distribution:')
print(high_range)
outer range (low) of the distribution:
[[-1.83820775]
[-1.83303414]
[-1.80044422]
[-1.78282123]
[-1.77400974]
[-1.62295562]
[-1.6166617 ]
[-1.58519209]
[-1.58519209]
[-1.57269236]]
outer range (high) of the distribution:
[[3.82758058]
[4.0395221 ]
[4.49473628]
[4.70872962]
[4.728631 ]
[5.06034585]
[5.42191907]
[5.58987866]
[7.10041987]
[7.22629831]]
# 重新繪製GrLivArea和SalePrice的散點圖
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000));
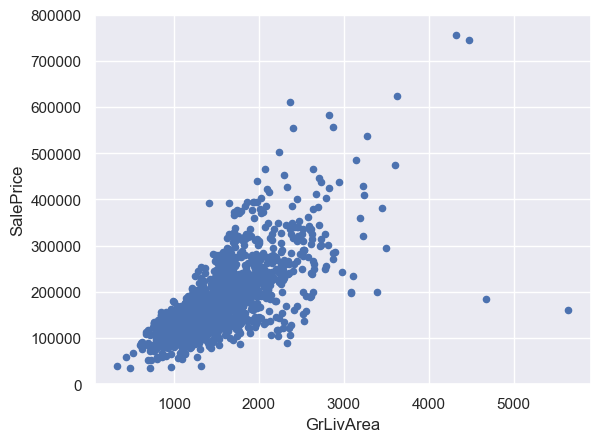
上圖中右下角的兩個點是異常值,因為它們的GrLivArea很大,但是售價很低。因此將它們刪除。
lines = df_train.sort_values(by='GrLivArea', ascending=False)[:2]
df_train = df_train.drop(lines.index)
5. 測試數據
對於結果的計算分析,需要建立在一定的數據假設上。通常,需要考慮這四種情況:
- 正態性(Normality):許多的統計方法測試都是基於數據是正態分佈的情況,因此,如果數據服從正態分佈能避免很多問題。
- 同方差性(Homoscedasticity):同方差性是指因變數的方差在自變數的每個水平上都相等。同方差性是許多統計檢驗的一個前提條件,如果數據不符合同方差性,可能會導致結果不准確。
- 線性性(Linearity):線性模型的一個前提條件是自變數和因變數之間的關係是線性的,如果不是線性的,可能需要對數據進行轉換。
- 不存在相關錯誤(Absence of correlated errors):相關錯誤是指數據中的一個觀測值的誤差與另一個觀測值的誤差相關。例如,如果兩個觀測值的誤差都是正的,那麼它們之間就存在正相關錯誤。相關錯誤可能會導致結果不准確。
from scipy.stats import norm
from scipy import stats
# 繪製直方圖與正態概率圖
sns.distplot(df_train['SalePrice'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)
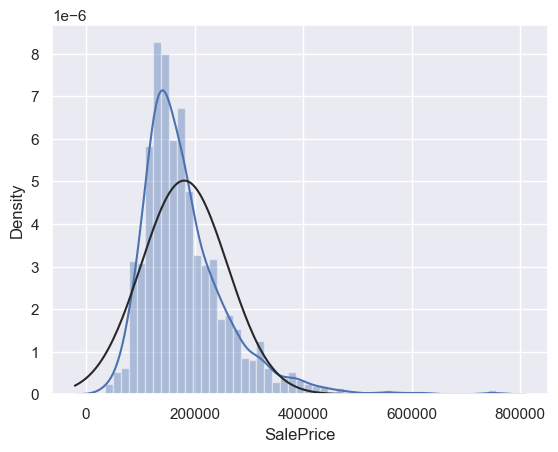
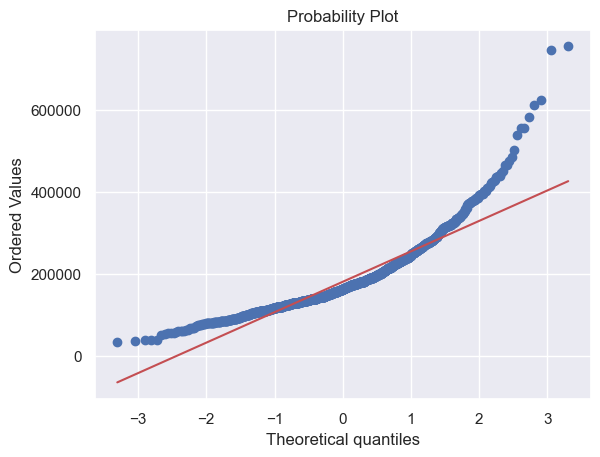
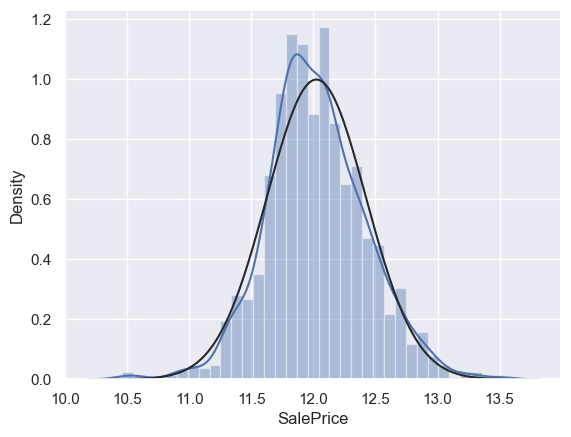
# 對SalePrice進行log轉換使其更接近正態分佈,並重新繪製直方圖與正態概率圖
df_train['SalePrice'] = np.log(df_train['SalePrice'])
sns.distplot(df_train['SalePrice'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)
# 同理,對GrLivArea繪製直方圖與正態概率圖
sns.distplot(df_train['GrLivArea'], fit=norm)
fig = plt.figure()
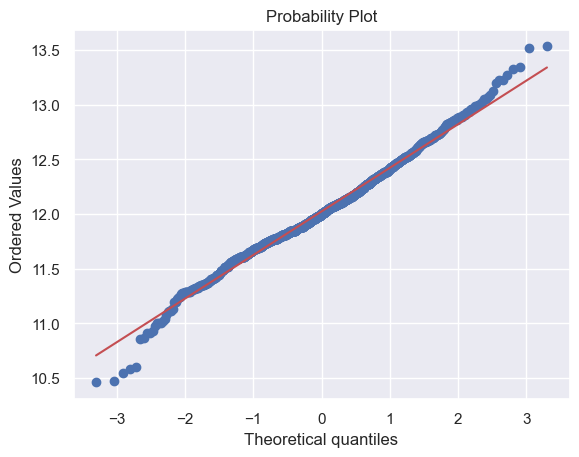
res = stats.probplot(df_train['GrLivArea'], plot=plt)
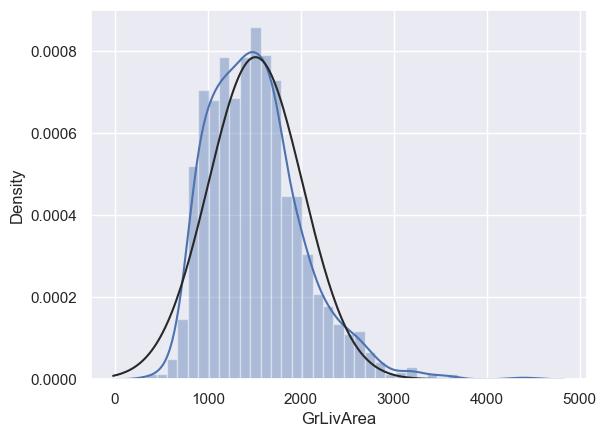
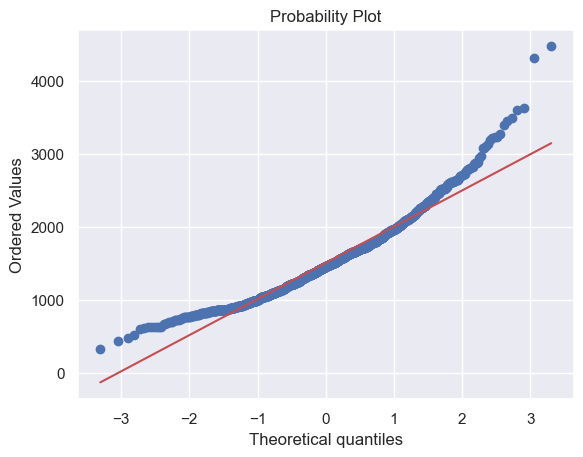
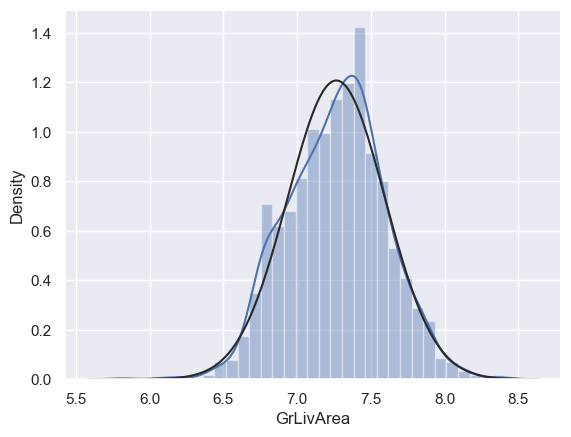
# 對GrLivArea進行log轉換使其更接近正態分佈,並重新繪製直方圖與正態概率圖
df_train['GrLivArea'] = np.log(df_train['GrLivArea'])
sns.distplot(df_train['GrLivArea'], fit=norm)
fig = plt.figure()
res= stats.probplot(df_train['GrLivArea'], plot=plt)
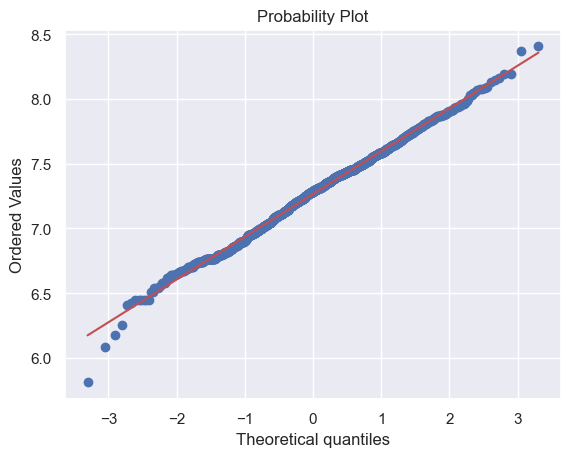
# 還有TotalBsmtSF
sns.distplot(df_train['TotalBsmtSF'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['TotalBsmtSF'], plot=plt)
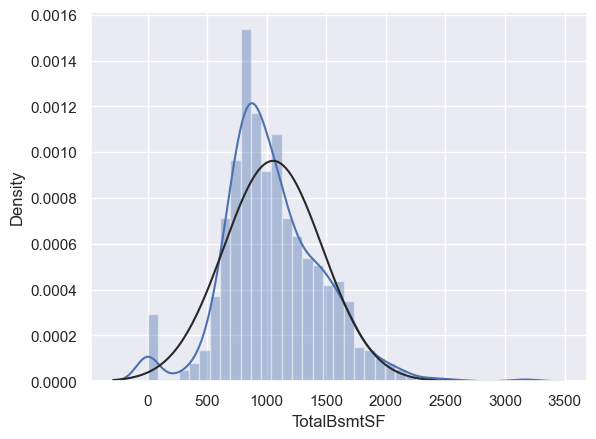
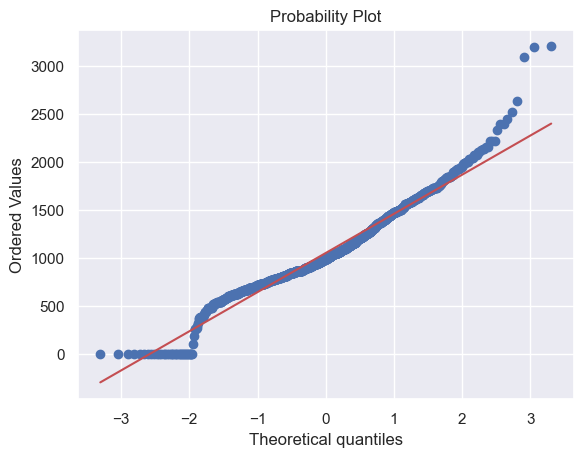
由於一些房子沒有地下室,導致有很多0值,因此不能對TotalBsmtSF進行log轉換。
這裡創建一個新的變數,如果TotalBsmtSF>0,則為1,否則為0。
df_train['HasBsmt'] = pd.Series(len(df_train['TotalBsmtSF']), index=df_train.index)
df_train['HasBsmt'] = 0
df_train.loc[df_train['TotalBsmtSF'] > 0, 'HasBsmt'] = 1
# 對HasBsmt為1的數據進行log轉換
df_train.loc[df_train['HasBsmt'] == 1, 'TotalBsmtSF'] = np.log(df_train['TotalBsmtSF'])
sns.distplot(df_train[df_train['TotalBsmtSF'] > 0]['TotalBsmtSF'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train[df_train['TotalBsmtSF'] > 0]['TotalBsmtSF'], plot=plt)
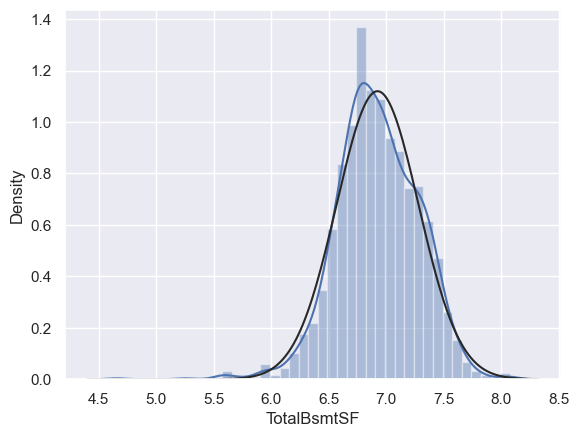
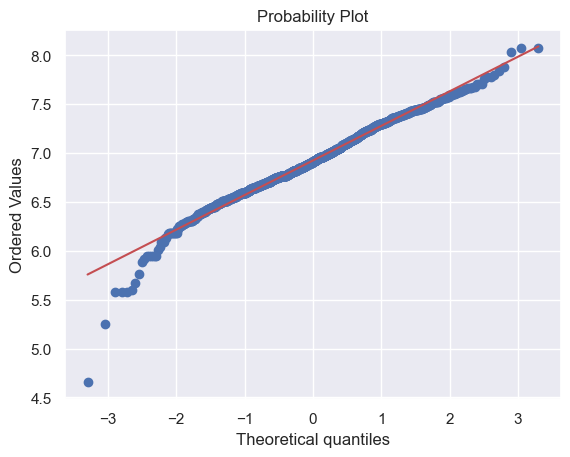
對於同方差的檢驗,可以繪製散點圖。如果散點呈現錐形(就像之前畫的),這意味著數據的方差隨著自變數的增加而增加,通常被稱為異方差;變數是同方差,散點的數據應該分佈在一條直線附近。
現在我們來看一下經過log運算後的SalePrice和GrLivArea還有TotalBsmtSF的散點圖。
plt.scatter(df_train['GrLivArea'], df_train['SalePrice']);
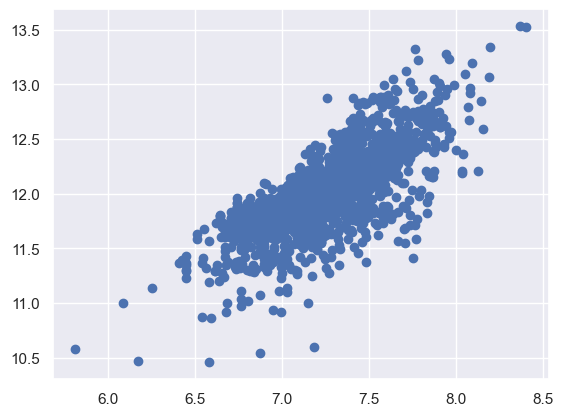
plt.scatter(df_train[df_train['TotalBsmtSF'] > 0]['TotalBsmtSF'], df_train[df_train['TotalBsmtSF'] > 0]['SalePrice']);
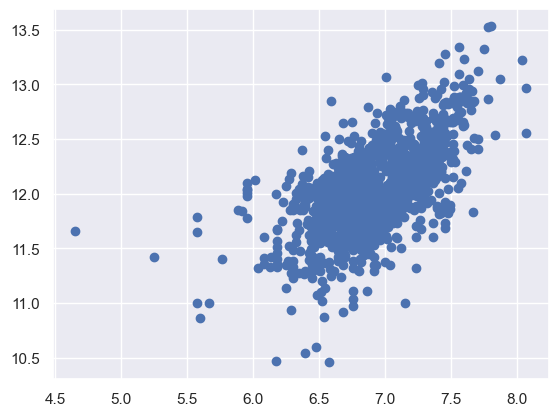
6. 啞變數
# 將類別變數轉換為啞變數
df_train = pd.get_dummies(df_train)
總結
本次使用了pandas庫和seaborn庫對數據進行了初步的分析,對數據的缺失值進行了處理,對數據進行了轉換,最後將類別變數轉換為啞變數。


