LeetCode的hard題都很難嗎?不一定,297就非常簡單,隨本文一起,用最基礎的知識寫代碼,執行用時能擊敗98.46%,與此同時,記憶體消耗擊敗99.73% ...
本篇概覽
- 因為欣宸個人水平有限,在刷題時一直不敢面對hard級別的題目,生怕出現一杯茶一包煙,一道hard做一天的窘境

- 這種恐懼心理一直在,直到遇見了它:LeetCode297,建議不敢做hard題的新手們速來圍觀,拿它練手,輕鬆找到自信
題目簡介
-
- 二叉樹的序列化與反序列化
序列化是將一個數據結構或者對象轉換為連續的比特位的操作,進而可以將轉換後的數據存儲在一個文件或者記憶體中,同時也可以通過網路傳輸到另一個電腦環境,採取相反方式重構得到原數據。
請設計一個演算法來實現二叉樹的序列化與反序列化。這裡不限定你的序列 / 反序列化演算法執行邏輯,你只需要保證一個二叉樹可以被序列化為一個字元串並且將這個字元串反序列化為原始的樹結構。
提示: 輸入輸出格式與 LeetCode 目前使用的方式一致,詳情請參閱 LeetCode 序列化二叉樹的格式。你並非必須採取這種方式,你也可以採用其他的方法解決這個問題。
- 提示
提示:
樹中結點數在範圍 [0, 104] 內
-1000 <= Node.val <= 1000
- 接下來,先開始輕鬆愉快的分析工作
分析
- 小結一下題目要求,需要做兩件事:
- serialize方法:輸入二叉樹根節點,返回字元串
- deserialize方法:輸入字元串,方法內部根據字元串構建一棵二叉樹,然後返回根節點
- 說實話,當時讀題後的第一反應是:這是二叉樹的基本操作嘛,一定是個easy,結果發現官方設定的難度是hard,當時就覺得賺大了!!!
- 簡單的說,解題思路只有四個字:前序遍歷
- 前序遍歷是啥?很簡單,是指一種遍歷二叉樹的順序,看著下麵的圖,咱們一起默念:根左右,所以前序遍歷下圖二叉樹的結果是:1,2,3
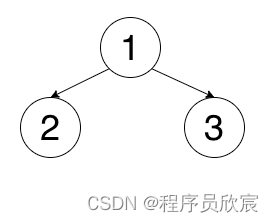
- 類似的還有中序遍歷,中序遍歷要求根節點在輸出位置的中間,也就是左根右,還是上面那個二叉樹,中序遍歷的結果是:2,1,3
- 還有後續遍歷是左右根,上面那個二叉樹,後序遍歷的結果是:2,3,1
- 至於本題為何要選前序遍歷,因為字元串轉二叉樹時,會涉及到數組,而將根節點放在數組的最前面,這樣既便於處理也便於理解
- 再來看看前序遍歷的代碼一般怎麼寫?或者說套路是什麼?
- 偽代碼如下,可見是個非常簡單的遞歸操作
private void dfs(TreeNode root) {
// 終止條件是發現入參為空
if(null==root) {
return;
}
// 1. 根
處理root的代碼
// 2. 左
dfs(root.left);
// 3. 右
dfs(root.right);
}
- 以前面那個圖上的二叉樹為例,分析上述代碼如何執行:調用dfs的時候傳入的是根節點,在dfs方法中,處理完根節點後,立即調用dfs處理左節點,在處理左節點的時候還會再遞歸一次,不讓過左節點的子節點都是null,所以這個遞歸啥事也沒做,處理完左節點後再調用dfs處理右節點,這樣就完成了根左右的處理
- 沒錯,二叉樹遍歷的套路就是這麼簡單,至於中序和後續遍歷的代碼,和上面的差不多,無非是將三段代碼的調用順序調整一下即可
- 接下來,編碼
編碼:序列化
- 先看序列化的代碼
- 首先準備一個StringBuilder類型的成員變數serializeRes,遍歷到的每一個元素都存放在serializeRes的尾部,用逗號分隔
private StringBuilder serializeRes;
- 然後是serialize方法的實現,首先要判斷root為空的特殊情況,另外就是serializeRes的初始化,然後就會調用serializeDfs方法,這個serializeDfs就是遍歷二叉樹的具體實現
public String serialize(TreeNode root) {
if (null==root) {
return null;
}
serializeRes = new StringBuilder();
serializeDfs(root);
return serializeRes.toString();
}
- 遍歷二叉樹的核心邏輯,serializeDfs方法如下,可見和咱們剛纔的偽代碼很像,每一個節點都會被存入serializeRes,並且以逗號分隔,只有一處需要註意,就是每當遇到root等於null,就在serializeRes尾部追加一個n,這樣在serializeRes中就相當於每個節點沒有左子節點或者右子節點的標誌,這很重要!
private void serializeDfs(TreeNode root) {
if(null==root) {
serializeRes.append("n,");
return;
}
// 1. 根
serializeRes.append(root.val).append(",");
// 2. 左
serializeDfs(root.left);
// 3. 右
serializeDfs(root.right);
}
- 以前面圖中那個最簡單的二叉樹為例是,上述代碼輸出的字元串內容如下,3在2,n,n之後,顯然是將2和2的子節點都處理完畢後,才去處理3,這就是典型的根左右:
1,2,n,n,3,n,n,
編碼:反序列化
- 接下來的反序列化,也是嚴格準守根左右的順序實現的,關鍵是註意對字元n的處理,它表示一個節點沒有左子節點或者右子節點了
- 首先是兩個環境變數,deserializeArray是個數組,字元串用逗號分割之後生成的數組,代表整個要恢復的二叉樹的所有元素,deserializeOffset用於記錄數組中已經有多少個元素已經被回覆到二叉樹中了:
private String[] deserializeArray;
private int deserializeOffset;
- 然後是最外層的發序列化方法,可見首先是處理異常邏輯,然後就會用字元串分割生成數組,再調用構建二叉樹的核心邏輯deserializeDfs:
public TreeNode deserialize(String data) {
if (null==data) {
return null;
}
deserializeArray = data.split(",");
deserializeOffset = 0;
return deserializeDfs();
}
- 最後看構建二叉樹的核心邏輯deserializeDfs方法,不要以為構建二叉樹的代碼會比遍歷二叉樹的代碼複雜,仔細看,發現還是嚴格準守根左右的順序去處理的,先生成根節點,然後遞歸生產左子樹和右子樹,要註意的地方就是遇到字元n的時候就不要繼續遞歸了,深度上已經到底了,需要返回上層,完成上層左子節點和右子節點的創建:
private TreeNode deserializeDfs() {
if (deserializeOffset>=deserializeArray.length) {
return null;
}
if ("n".equals(deserializeArray[deserializeOffset])) {
deserializeOffset++;
return null;
}
// 1. 根
TreeNode treeNode = new TreeNode(Integer.valueOf(deserializeArray[deserializeOffset++]));
// 2. 左
treeNode.left = deserializeDfs();
// 3. 右
treeNode.right = deserializeDfs();
return treeNode;
}
- 最後貼出完整的代碼
public class Codec {
// 本題的整體思路是前序遍歷,即:根左右
private StringBuilder serializeRes;
private String[] deserializeArray;
private int deserializeOffset;
private void serializeDfs(TreeNode root) {
if(null==root) {
serializeRes.append("n,");
return;
}
// 1. 根
serializeRes.append(root.val).append(",");
// 2. 左
serializeDfs(root.left);
// 3. 右
serializeDfs(root.right);
}
private TreeNode deserializeDfs() {
if (deserializeOffset>=deserializeArray.length) {
return null;
}
if ("n".equals(deserializeArray[deserializeOffset])) {
deserializeOffset++;
return null;
}
// 1. 根
TreeNode treeNode = new TreeNode(Integer.valueOf(deserializeArray[deserializeOffset++]));
// 2. 左
treeNode.left = deserializeDfs();
// 3. 右
treeNode.right = deserializeDfs();
return treeNode;
}
// Encodes a tree to a single string.
public String serialize(TreeNode root) {
if (null==root) {
return null;
}
serializeRes = new StringBuilder();
serializeDfs(root);
return serializeRes.toString();
}
// Decodes your encoded data to tree.
public TreeNode deserialize(String data) {
if (null==data) {
return null;
}
deserializeArray = data.split(",");
deserializeOffset = 0;
return deserializeDfs();
}
}
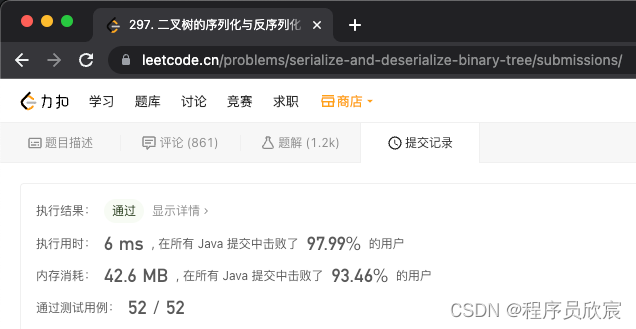
- 提交代碼,如下圖,順利AC,速度超97%,同時記憶體超93%,感覺美滋滋的,這可個是一道hard呀!
小幅度優化
- 回顧此題,似乎還有一丁點優化空間:在序列化的時候,咱們用字元n作為子節點為空的標誌,例如
1,2,n,n,3,n,n,
- 如果用空字元串取代n,那豈不是省掉了一些空間?
- 說乾就乾,一共有兩處,第一處在序列化的時候,用n做結束標誌的那段代碼,改動如下圖

- 第二處是反序列化的時候,判斷是否為n的那段代碼,改動如下圖
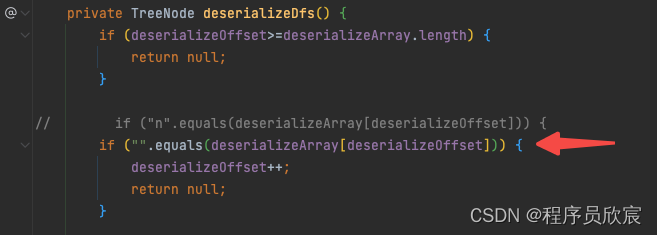
- 改完提交代碼,效果如下圖,速度和記憶體都有小幅度優化,第一次距離雙百這麼近!
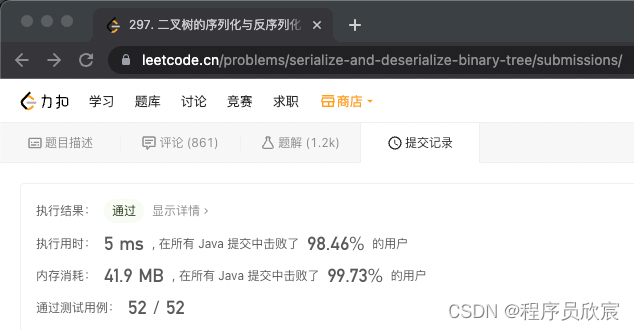
- 至此,297的分析和實戰已經完成,hard題能如此簡單,實屬不易遇到,所以不要錯誤哦,希望本文能給您一些思路,助您用最基礎的代碼,跑出最耀眼的成績



