AC 自動機學習筆記

前言

AC自動機（\(Aho\ Corasick\ Atomaton\)）有著一種 \(KMP\) 的思想，所以在學習之前建議先學一下 \(KMP\)。同時還需要瞭解一下 \(Trie\) 樹（建議去看一下 oi-wiki 上的字典樹）

問題描述

給定一個字元串 \(S\) 和 \(n\) 模式串，問有多少個模式串在 \(S\) 中出現過。

首先我們把 \(n\) 個模式串組成一個 \(Trie\)（就當你們學會了 \(Trie\) 樹）

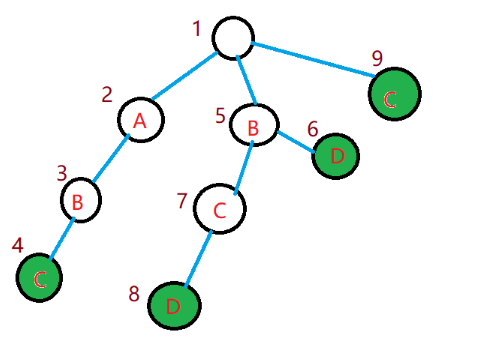
模式串：\(ABC,BCD,BD,C\)，其中綠色的點表示字元串的結尾。

對於 \(|S|=ABCBCD\)，那麼我們在 \(Trie\) 上開始匹配，最開始會經過 \(2,3,4\) 三個點到 \(4\) 的時候，發現已經成功匹配了一個模式串了，那麼現在我們需要從根在匹配一次嗎？

顯然的，不需要，\(KMP\) 的思想可以運用在這個 \(Trie\) 樹上，我們在匹配完 \(4\) 的時候可以直接來到 \(7\) 然後再匹配到 \(8\)。

對於從 \(4\) 到 \(7\) 這個步驟，我們稱 \(7\) 是 \(4\) 的 \(Fail\)（失配指針）。

\(Fail\) 指針

剛纔說了 \(Fail\) 是失配指針，那麼如果此時匹配失敗，那麼就到達這個指針指向的位置，所以，失配指針指向的節點是當前節點所代表的串，最長的、能與尾碼匹配的，且在 \(Trie\)
中出現過的首碼所代表的節點。

我們設點 \(x\) 的父親的 \(Fail\) 指針指向的是 \(p\)，那麼如果 \(p\) 的兒子 \(y\) 和 \(x\) 相同，那麼 \(x\) 的 \(Fail\) 指針指向的就是 \(y\)（應該挺好理解的吧）。

那麼如果沒有兒子呢？

那就再造一個兒子，就把當前節點的子節點指向當前節點的 \(fail\) 節點的子節點。

而且發現每個點 \(fail\) 指向的節點都比當前節點小，那麼第二層的 \(fail\) 就指向根節點。

然後對於失配指針 \(Fail\) 我們需要使用 \(BFS\) 來實現。

inline void Get_fail(){
	for(int i=0;i<26;i++)
		if(ch[0][i])
			q.push(ch[0][i]),fail[ch[0][i]]=0;
	while(!q.empty()){
		int u=q.front();
		q.pop();
		for(int i=0;i<26;i++)
			if(ch[u][i]) fail[ch[u][i]]=ch[fail[u]][i],q.push(ch[u][i]);
			else ch[u][i]=ch[fail[u]][i];//沒有子節點，就把當前節點的子節點指向當前節點的fail節點的子節點
	}
}

查詢

首先，指針指向根節點，依次讀入單詞，檢查是否存在這個子節點。

然後指針跳轉到子節點，如果不存在，直接跳轉到失配指針即可。

inline int query(string s){
	int len=s.size(),v=0,res=0;
	for(int i=0;i<len;i++){
		v=ch[v][s[i]-'a'];
		for(int j=v;j&&val[j]>=0;j=fail[j]){
			res+=val[j];
			val[j]=-1;
		}
	}
	return res;
}

時間複雜度：\(O(|\Sigma|M)\)（\(| \Sigma |\) 一般來說是 \(26\)）$。