請享用美味的快速冪演算法-通俗易懂版

一、演算法整體思路

第1步

　　按照最直接、最好理解的方式看，2的n次冪是n個2相乘，即有如下公式

　　例如：

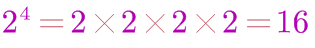
第2步
　　然而為了節省大量時間，通過簡單的思考和嚴格數學推理，我們不難理解以下結論：
　　1.偶數冪的情況:
　　　　通過冪函數運演算法則，有2ⁿ=（2^n/2）²，即有如下等式：

　　　　例如2⁴　的計算過程如下所示：

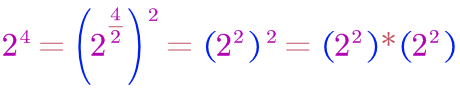
　　　　得到上面的表達式後，2²是不是可以繼續按照這個思想分解下去？of course！現在只是舉了一個4次方的例子，我們可以從此得到啟發，發現求n次冪最終可以歸結為不斷的重覆這個分解的一個過程，直到冪不能分解（冪為0了）才停下來。

　　　　由此，上述過程可以描述為一個遞歸過程，遞歸基（遞歸結束條件）為”冪等於0“。得到以下遞歸表達式：

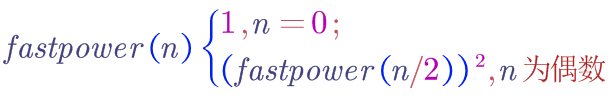
　　小插敘：

　　　　解釋第二種情況前，有必要說明以下內容，這也是為什麼第二種情況存在的原因：

　　　　如果n是奇數，我們知道，在電腦中，n/2會捨去小數，這樣如果繼續按照上述第一步的方法分解，逆推回去，會發現最終得到的冪是n-1；不信，且看下例

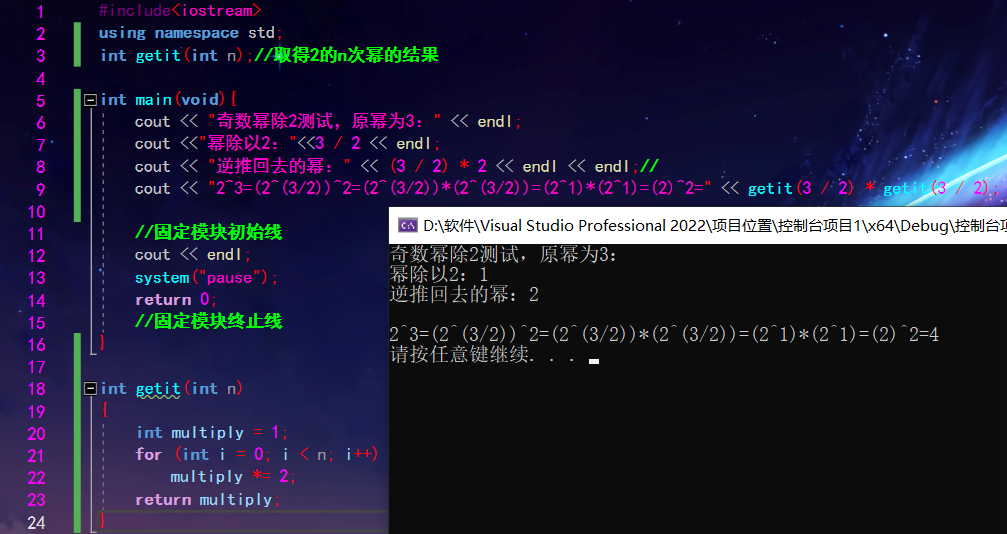
　　2.奇數冪的情況：

　　　　好了，現在可以引出第二種情況，就是奇數冪的情況。我們要求得奇數冪的結果，可以從繼續步驟1,即按照偶數冪的求法求出最終結果，再附加一個條件是，什麼條件呢？

　　　　就是在原來的結果上乘上一個2，原因我相信在插敘中已經說的很明白了，它少了1次冪，現在是在補上這一次冪，即：

 　　3.最終遞歸表達式

　　　　那麼到現在，我們可以寫出完整的遞歸表達式了，在偶數冪的遞歸條件下，附加奇數冪的條件即可，即：

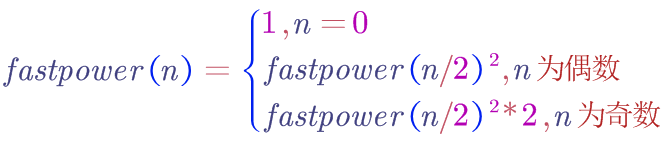
第3步

　　我們現在對於快速冪的求解思路應當是已經十分清晰了，現在我們來寫遞歸函數(C++):

long long int fastpower(int n){
    if (n == 0)//遞歸基
        return 1;
    else if (n % 2 == 0)//偶數冪的情況
        return square(fastpower(n / 2));
    else//奇數冪的情況
        return square(fastpower(n / 2)) * 2;
}
long long int square(long long int t){
    return t * t;
}

二、上刑
　　everybody，現在我們已經完全理清了思路，接下來要把它整成代碼吧！

#include<iostream>
using namespace std;

long long int fastpower(int n);//求解快速冪
long long int square(long long int t);//平方

int main(void){

    int n;
    cin >> n;//輸入冪
    cout << fastpower(n);

    //固定模塊初始線
    cout << endl;
    system("pause");
    return 0;
    //固定模塊終止線
}

long long int fastpower(int n){
    if (n == 0)//遞歸基
        return 1;
    else if (n % 2 == 0)//偶數冪的情況
        return square(fastpower(n / 2));
    else//奇數冪的情況
        return square(fastpower(n / 2)) * 2;
}
long long int square(long long int t){
    return t * t;
}

希望能幫助到你，祝你學有所成！