數學上有一個“計算漢明重量”的問題,即求取一個二進位位中非 0 的數量。使用 Redis 提供的 Bitmap 統計時恰恰是這樣一個問題,學習後能發現解決辦法卻是如此巧妙。 ...
簡介
Redis 使用字元串對象來表示位數組,因為字元串對象使用的 SDS 數據結構是二進位安全的,所以程式可以直接使用 SDS 結構來保存位數組,並使用 SDS 結構的操作函數來處理位數組。
在 SDS 結構當中,buf 位元組數組除了字元串結尾的 \0 空字元,其餘的位置都存儲著一個位元組長的位數組,一個位元組可以存儲 8 位的二進位。
這裡需要註意的是,在 buf 數組中存儲的二進位位數組的順序與實際書寫的順序相反,比如 01010101 存儲在 buf 數組中的結構是 10101010 這樣的倒序,使用逆序來保存位數組可以簡化 SETBIT 的實現。
命令使用
Redis 提供了 GETBIT、SETBIT、BITCOUNT、BITOP、BITPOS、BITFIELD、BITFIELD_RO 等命令用於處理二進位位數組。
GETBIT
GETBIT <bitarray> <offset> 命令用於返回位數組 bitarray 在 offset 偏移量上的二進位位的值。其詳細執行過程如下:
- 計算
byte = offset / 8得到offset偏移量指定的二進位位保存在位數組的哪個位元組; - 計算
bit = (offset mod 8) + 1得到offset偏移量指定的二進位位是byte位元組的第幾個二進位位; - 根據
byte值和bit值,在位數組bitarray中定位offset偏移量指定的二進位位,並返回這個位的值。
SETBIT
SETBIT <bitarray> <offset> <value> 可以看作是 GETBIT 的反向操作,只是需要註意設置二進位位時有可能需要擴展 buf 數組的長度。
具體的執行過程如下:
- 計算
len = (offset / 8) + 1得到保存offset偏移量指定的二進位位需要多少位元組; - 檢查
bitarray位數組的長度是否滿足要求,否則需要對 SDS 的進行擴展,並且將新增的二進位位全部置為 0; - 計算
byte = offset / 8得到offset偏移量指定的二進位位保存在位數組的哪個位元組; - 計算
bit = (offset mod 8) + 1得到offset偏移量指定的二進位位是byte位元組的第幾個二進位位; - 根據
byte值和bit值,在位數組bitarray中定位offset偏移量指定的二進位位,首先將這個位現在的值保存在oldvalue變數中,然後將新值value設置為這個二進位位的值; - 向客戶端返回
oldvalue的值。
由於 buf 數組使用逆序保存位數組,當 Redis 對 buf 數組進行擴展之後,寫入操作都可以直接在新擴展的二進位位中完成,而不必改動位數組原來已有的二進位位。
BITCOUNT
BITCOUNT key [start] [end] 命令用於統計給定位數組中,值為 1 的二進位位的數量。
BITOP
BITOP operation destkey key [key ...] 支持對一個或多個保存二進位位的字元串 key 進行位元操作,並將結果保存到 destkey 上。operation 可以是 AND 、 OR 、 NOT 、 XOR 這四種操作中的任意一種:
AND: 邏輯與OR: 邏輯或NOT: 邏輯非XOR: 邏輯異或
因為 BITOP AND、BITOP OR、BITOP XOR 三個命令可以接受多個位數組作為輸入,程式需要遍歷輸入的每個位數組的每個位元組來進行計算,所以這些命令的複雜度為 \(O(n^2)\);與此相反,因為 BITOP NOT 命令只接受一個位數組輸入,所以它的複雜度為 \(O(n)\)。
BITPOS
BITPOS key bit [start [end [BYTE | BIT]]] 返回字元串中設置為 1 或 0 的第一個位的位置。
預設情況下,整個字元串都會被檢索一遍。命令的
使用 start 和 end 參數預設可以指定一個位元組的範圍,在 7.0.0 版本之後,提供了 BYTE 和 BIT 指定以位元組為範圍還是位為範圍。
二進位位統計演算法
BITCOUNT 命令要做的工作初看上去並不複雜,但實際上要高效地實現這個命令並不容易,需要用到一些精巧的演算法。
遍歷演算法
實現 BITCOUNT 命令最簡單直接的方法,就是遍歷位數組中的每個二進位位,併在遇到值為 1 的二進位位時,將計數器的值增一。
遍歷演算法雖然實現起來簡單,但效率非常低,因為這個演算法在每次迴圈中只能檢查一個二進位位的值是否為 1,所以檢查操作執行的次數將與位數組包含的二進位位的數量成正比。
查表演算法
查表演算法就是創建一個表,表的鍵為某種排列的位數組,而表的值則是相應位數組中值為 1 的二進位位的數量。
創建了這種表之後,就可以根據輸入的位數組進行查表,在無須對位數組的每個位進行檢查的情況下,直接知道這個位數組包含了多少個值為 1 的二進位位。
初看起來,只要創建一個足夠大的表,那麼統計工作就可以輕易地完成,但這個問題實際上並沒有那麼簡單,因為查表法的實際效果會受到記憶體和緩存兩方面因素的限制:
- 查表法是典型的空間換時間策略,演算法在計算方面節約的時間是通過花費額外的記憶體換取而來的,節約的時間越多,花費的記憶體就越大。
- 查表法的效果還會受到 CPU 緩存的限制,對於固定大小的 CPU 緩存來說,創建的表格越大,CPU 緩存所能保存的內容相比整個表格的比例就越少,查表時出現緩存不命中的情況就會越高,緩存的換入和換出操作就會越頻繁,最終影響查表法的實際效率。
variable-precision SWAR 演算法
BITCOUNT 命令要解決統計一個位數組中非 0 二進位位的數量的問題,在數學上被稱為“計算漢明重量(Hamming Weight)”。目前已知效率最好的通用演算法為 variable-precision SWAR 演算法,該演算法通過一系列位移和位運算操作,可以在常數時間內計算多個位元組的漢明重量,並且不需要使用任何額外的記憶體。
以下是一個處理 32 位長度位數組的 variable-precision SWAR 演算法的實現:
uint32_t swar(uint32_t i){
i = (i & 0x55555555) + ((i>>1) & 0x55555555); // 步驟 1
i = (i & 0x33333333) + ((i>>2) & 0x33333333); // 步驟 2
i = (i & 0x0F0F0F0F) + ((i>>4) & 0x0F0F0F0F); // 步驟 3
i = (i - 0x01010101) >> 24; // 步驟 4
return i;
}
variable-precision SWAR 演算法實質上是通過分而治之的思想,將計算拆解成多個小問題去解決:
- 步驟 1 是將 32 位數組與
01010101010101010101010101010101做邏輯與操作,並且右移 1 位之後繼續做邏輯與操作,最終取它們的和。這一步的想法是將 32 位拆成每 2 位作為一個組合,統計出每一組中 1 的個數; - 步驟 2 是將上述得到的結果與
00110011001100110011001100110011做邏輯與操作。這一步的想法就是拆成每 4 位作為一個組合,統計出每一組中 1 的個數; - 步驟 3 是將上述得到的結果與
00001111000011110000111100001111做邏輯與操作。這一步的想法就是拆成每 8 位作為一個組合,統計出每一組中 1 的個數; - 上述的結果仍然不是最終想要的結果,步驟 4 就是將上述得到的數字計算出 1 真正的數量。
i - (0x01010101)計算出漢明重量並記錄在二進位的高八位,>> 24語句則通過右移運算,將漢明重量移到最低八位,最後二進位對應的十進位就是漢明重量。
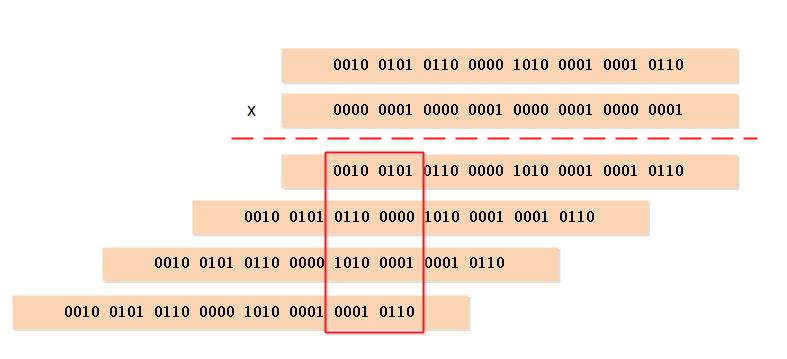
因為 variable-precision SWAR 演算法是一個常數複雜度的操作,所以可以按照自己的需要,在一次迴圈中多次執行 variable-precision SWAR 演算法,從而按倍數提升計算漢明重量的效率。
當然,在一個迴圈里執行多個 variable-precision SWAR 演算法調用這種優化方式是有極限的:一旦迴圈中處理的位數組的大小超過了緩存的大小,這種優化的效果就會降低並最終消失。
Redis 的實現
BITCOUNT 命令的實現用到了查表和 variable-precision SWAR 兩種演算法:
- 如果未處理處理的二進位位的數量小於 128 位,那麼程式使用查表演算法來計算二進位位的漢明重量,表中記錄了 0x00 ~ 0xFF 在內的所有二進位位的漢明重量
- 如果未處理的二進位位的數量大於等於 128 位,那麼程式使用 variable-precision SWAR 演算法來計算二進位位的漢明重量,每次處理 128 個二進位位,調用 4 次 32 位 variable-precision SWAR 演算法來計算其漢明重量
實際上 BITCOUNT 命令實現的演算法複雜度為 \(O(n)\),其中 n 為輸入二進位位的數量。



