首碼和 一、介紹 ~~首碼,顧名思義就是一個東西前面的點綴...~~(bushi 其實打比方來說就是:假如有一字元串ABCD,那麼他的首碼就是A、AB、ABC、ABCD這四個從新從第一個字母一次往後開始拼接的字元串。當然這是字元串。但首碼和一般應用於數組,對於給定的數組a=[1,2,3,4],他的前 ...
首碼和
一、介紹
首碼,顧名思義就是一個東西前面的點綴...(bushi
其實打比方來說就是:假如有一字元串ABCD,那麼他的首碼就是A、AB、ABC、ABCD這四個從新從第一個字母一次往後開始拼接的字元串。當然這是字元串。但首碼和一般應用於數組,對於給定的數組a=[1,2,3,4],他的前 i 項和sum[i]就表示數組中a[0]~a[i]的和,具體為:
sum[0]=a[0]
sum[1]=a[0]+a[1]
......
sum[i]=sum[0]+sum[1]+...+sum[i];
二、定義
定義:首碼和是指某一序列的前 n 項和。
基於首碼和的使用,我們一般把首碼和分為一維首碼和和二維首碼和。
三、一維首碼和
定義
基於一維數組的首碼和就是原數組前n個元素的和。
const int N = 10010;
int a[N]; //原數組a[]
int s[N]; //首碼和數組s[]
//根據定義 一維首碼和s[i]
s[i] = a[1] + a[2] + a[3] +...+ a[i];
//舉例 設i=3 根據上式可得
s[3] = a[1] + a[2] + a[3];
//根據上面舉例,可以再一步寫成
s[i] = s[i-1] + a[i];
需要註意的一點是:數組的下標都是從 1 開始的!!!
作用
主要作用是可以在O(1)時間情況下快速的求出任一區間[l,r]內的元素之和。
//例如求a[3]+...+a[10]之間的和,我們可以利用首碼和迅速求出:
a[3]+...+a[10]
= (a[1]+a[2]+a[3]...+a[10]) - (a[1]+a[2])
= s[10] - s[2]
//根據上面舉例,我們可以推導出求某一區間[l,r]內的和的公式
a[l]+a[l+1]+...+a[r-1]+a[r]
= s[r] - s[l-1];
方法
一維數組求首碼和方法
int a[100],s[100];
for(int i = 1; i<= 99; i++)
{
scanf("%d",&a[i]);
}
for(int i = 1; i<= 99; i++)
{
s[i] = s[i-1]+a[i];
}
實戰演練!!!
「模板」首碼和
輸入n個數,給出m個詢問,詢問區間[x,y]的和。
輸入
-
第一行為n和m,1<=n,m<=100000
-
接下來一行為n個數,範圍在0~100000之間
-
接下來m行,每行兩個數x,y,輸出第x個數到第y個數之間所有數的和。保證x<=y
輸出
m個輸出
樣例輸入
5 3
1 2 0 7 6
1 3
2 2
4 5
樣例輸出
3
2
13
代碼:
#include <bits/stdc++.h>
using namespace std;
int n,m;
long long a[100010],b[100010];//見註釋1
int main()
{
cin >> n >> m;
for(int i=1; i<=n;i++)
{
cin >> a[i];
}
b[0]=0;
for(int i=1;i<=n;i++)
{
b[i]=b[i-1]+a[i];
}
while(m--)
{
int l,r;
cin >> l >> r;
cout << b[r] - b[l-1] << "\n";
}
return 0;
}
註釋①:測試範圍大
四、二維首碼和
定義
基於二維數組的首碼和,它是指一個前 i 行和前 j 列的子矩陣的和
const int N =100010;
int a[N][N] //原二維數組
int s[N][N] //二維首碼和數組
//根據定義可得
s[i][j] = a[1][1] + a[1][2] + ... + a[1][j]+
a[2][1] + 1[2][2] + ... + 1[2][j]+
a[3][1] + ... + ... + a[3][j]+
+ +
.... ....
+ +
a[i][1] + ... + ... + a[i][j]
作用
主要作用是可以在是可以在O(1)情況下求出任何子矩陣的和
圖解:
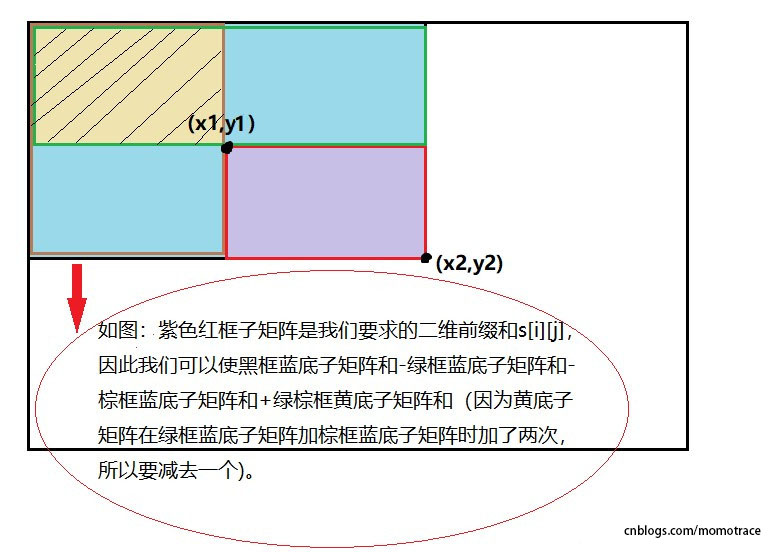
在這個矩陣(二維數組)中,我們要求上圖中紫色區域的和,現在我們已經預處理出了所有點的首碼和,現在給定兩個點\((x1,y1)\),\((x2,y2)\),我們需要求的是以這兩個點連線為對角線的一個子矩陣的數值之和。首先我們可以把\(s[x2][y2]\)求出來,它代表整個大矩形的首碼和,然後我們分別減去它右邊多出來的一塊的首碼和和上邊多出來一塊的首碼和,但是需要註意下邊的左上角被減了兩次,所以我們需要加回來一次。故對於一次的查詢是\(s[i][j]\)應該等於\(s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]\)。
- 所求子矩陣和=\(s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1]\);
方法
二維數組求首碼和方法
const int N = 10010;
int a[N][N],s[N][N]
//n,m為鍵盤輸入
for(int i = 1; i <= n; i++)
{
for(int j = 1;j <= m; j++)
{
scanf("%d",&a[i][j]);
}
}
for(int i = 1; i<= n; i++)
{
for(int j = 1; j <= m; j++)
{
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];
}
}
具體代碼!!!
#include <iostream>
const int N = 1010;
int n,m,q;
int a[N][N],s[N][N];
int main()
{
scanf("%d%d%d",&n,&m,&q);
for(int i = 1; i <= n; i++)
{
for(int j = 1;j <= m; j++)
{
scanf("%d",&a[i][j]);
}
}
for(int i = 1; i<= n; i++)
{
for(int j = 1; j <= m; j++)
{
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];
}
}
while(q--)
{
int x1,y1,x2,y2,re;
scanf("%d%d%d%d",&x1,&y2,&x2,&y2);
re = s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1];
printf("%d\n",re);
}
}
本文來自小默的博客,轉載請註明原文鏈接:https://www.cnblogs.com/momotrace/p/Prefix-sum.html



