牛客網BC115---超級聖誕樹(java)

和女朋友坐一塊的時候，突然想到了，哈哈哈哈哈

不會很難！！！

import java.util.*;

import java.lang.Math;

// 註意類名必須為 Main, 不要有任何 package xxx 信息
public class Main {
    public static void main(String[] args) {
        Scanner in = new Scanner(System.in);

        /**
		思考過程如下：
        小三角形個數為 3^(n-1)
        1 3 9 27
        3^(1-1) = 1
        3^(2-1) = 3
        3^(3-1) = 9
        3^(4-1) = 27
        3^(5-1) = 81

        // 去除桿子有多少層					用到了
        n
        3x1    3       3*2^(1-1)
        3x2    6       3*2^(2-1)
        3x4    12
        3x8    24
        3x16   48
        int allP = 3 * (int)Math.pow(2, n - 1);
        

        最底層三角形個數                	沒用到
        n
        1   1   0+1             2^(n-1)
        2   2   1+1             
        3   4   2+1+1
        4   8   4+2+1+1
        5   16  8+4+2+1+1
        6   32  16+8+4+2+1+1
        int lastPT = Math.pow(2, n - 1)

        最底層寬度  最底層三角形個數*6   	用到了
        n
        1 6   
        2 12  
        3 24
        4 48
        5 96
        int lastPW = (int)Math.pow(2, n - 1) * 6;
        24 - 3 - 12 - 0


        左邊寬 最底層寬度 - 6 / 2  每三行-3   用到了
        1 0
        2 3-0
        3 9-6-3-0
        4 21-18-15-12-9-6-3-0
        int leftW = (lastPW - 6) / 2;


        最底層判斷          需要
        int nowP = 0;
        int lastP = 3;
        int checkN = 1;
        if nowP = lastP
            checkN++;
            lastP += lastP



        第幾層，三角形大間隔    當checkN>2時，存在大間隔     最大間隔等於上一層最底層寬度-6
		!!!!用到了！
        int triW = 0;   // 初始值
        if (nowP == lastP) {
            checkN++;
            lastP += lastP;
            if (checkN > 2) {
                triW = ((int)Math.pow(2, checkN - 2) - 1) * 6;          //<----用到了這個
            }
            starN = 2;   // "  *   "、" * *  "、"* * * "每層數量
            starP = 0;   // 輸出了幾層了
        }
        n
        1 0
        2 0
        3 6-0       每三行-6         
        4 18-12-6-0                 
        5 42-36-30-24-18-12-6-0     
        if (nowP % 3 == 0) {
            triW -= 6;
            leftW -= 3;
        }


        // "  *   "、" * *  "、"* * * "每層
        starN = 2   // "  *   "、" * *  "、"* * * "每層數量
        starP = 1   // 輸出了幾層了
        if (starP % 4 == 0) starN *= 2;

        // 星與星間距
        2 2 2       3   3*1
        4
        4 4 4       6   3*2
        4 4 4       9   3*3
        10
        8 8 8       12  3*4
        8 8 8       15  3*5
        16
        16 16 16    18  3*6
        16 16 16    21  3*7
        22
        32 32 32    24  3*8

        int starW = (lastPW - starN * 6 - leftW - triW) / 2;
                    24 - 12 - 3 - 6
         */
	  
		/*
		觀察例子，可以發現，從n=2開始
		左右樹兩邊都是前者各層的形狀，故直接計算好整體左邊和左右兩邊樹間距即可實現了
		*/
        
        int n = in.nextInt();
        int lastPW = (int)Math.pow(2, n - 1) * 6;                   // 最底層寬度
        int leftW = (lastPW - 6) / 2;                               // 左邊寬 每三層-3
        int allP = 3 * (int)Math.pow(2, n - 1);                     // 去除桿子的總層數
        int checkN = 1;                                             // 檢測n，每個n對應的層數
        int starW = 0;                                              // 左右兩邊間距
        int starP = 0;                                              // 統計每新的開始輸出幾層了
        String[] treeData = new String[allP + n];                   // 樹
        for (int i = 1; i <= allP; i++) {
            for (int j = 0; j < leftW; j++) System.out.print(" ");	// 輸出左邊寬
            if (i < 4) {			// 相當於一個初始化的過程
                String putStr = "";
                if (i == 1) {
                    // "  *   "
                    putStr = "  *   ";
                } else if (i == 2){
                    // " * *  "
                    putStr = " * *  ";
                } else {
                    // "* * * "
                    putStr = "* * * ";
                }
                treeData[i - 1] = putStr;
                System.out.print(putStr);
            } else {				// 開始輸出前者的內容
                StringBuilder putStr = new StringBuilder();
                for (int j = 0; j < 2; j++) {	// 左右
                    putStr.append(treeData[starP]);
                    if (j == 0) {
                        // 輸出間距
                        for (int k = 0; k < starW; k++) {
                            putStr.append(" ");
                        }
                    }
                }
                System.out.print(putStr);
                treeData[i - 1] = putStr.toString();
            }
            System.out.println();

            starP++;
            if (i % 3 == 0) {	// 每三層，左邊寬度-3，左右兩邊樹的間距-6
                leftW -= 3;
                starW -= 6;
            }
		  	// 根據checkN知道當前輸出是否到達每個n所處的輸出範圍
            if ((int)Math.pow(2, checkN - 1) * 3 == i) {
                checkN++;
                starP = 0;											// 每個n(checkN)，就是新的開始
                if (checkN > 2) {
                    starW = (int)Math.pow(2, checkN - 2) * 6 - 6;	// 左右兩邊樹的間距計算
                }
            }
        }

        // 桿子
        int leftTW = (lastPW / 2) - 1;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < leftTW; j++) {
                System.out.print(" ");
            }
            System.out.println("*");
        }

    }
}

下麵附圖進一步理解:

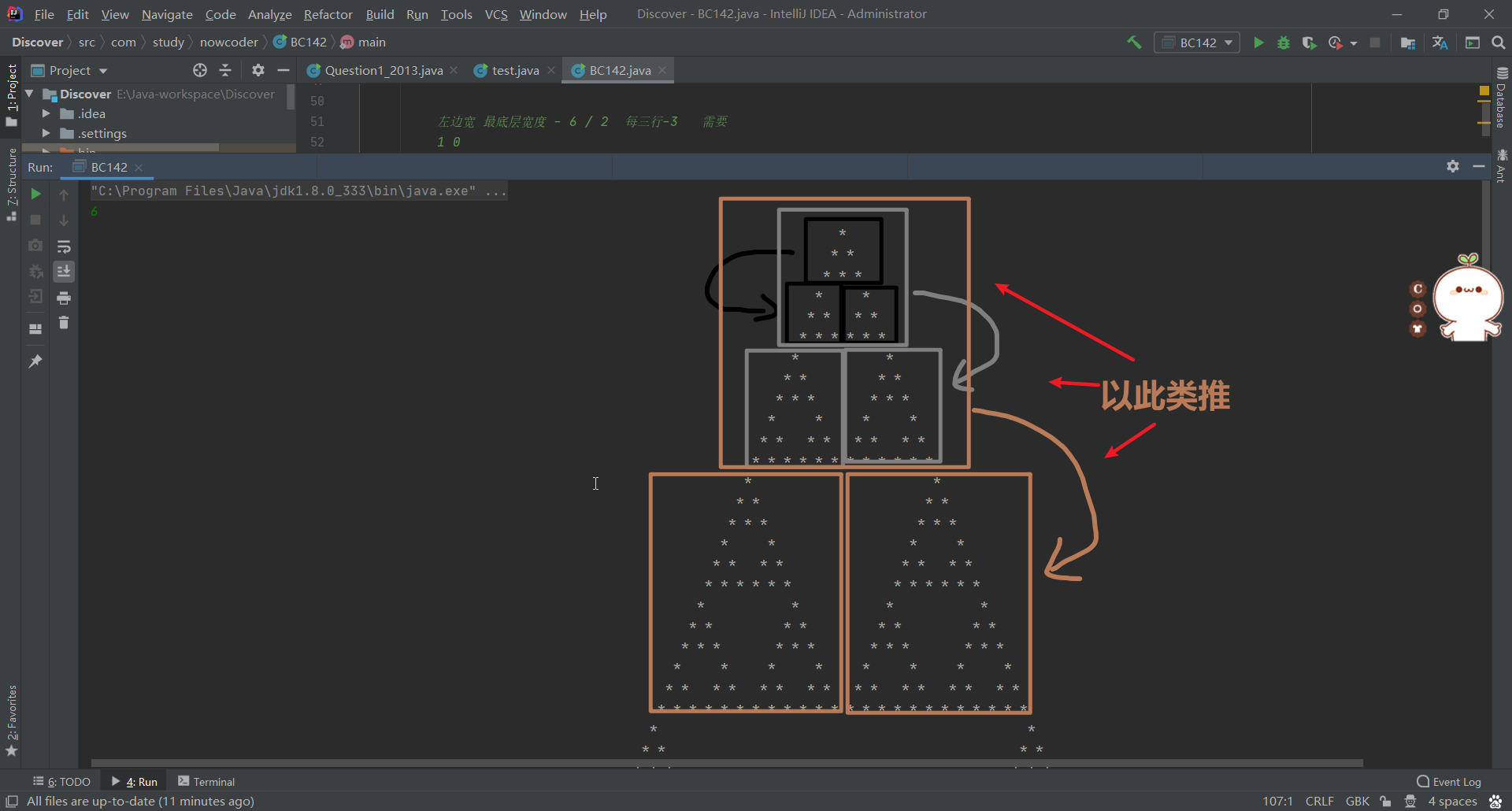
最後，感謝你閱讀我的文章，感恩！！！