當前主流編程語言的垃圾收集器基本上都是依靠可達性分析演算法來判定對象是否存活的，可達性分析演算法理論上要求全過程都基於一個能保障一致性的快照中才能夠進行分析，這意味著必須全程凍結用戶線程的運行。

• 在根節點枚舉這個步驟中，由於 GC Roots 相比起整個 Java 堆中全部的對象畢竟還算是極少數，且在各種優化技巧（如 OopMap）的加持下，它帶來的停頓已經是非常短暫且相對固定（不隨堆容量而增長） 的了。
• 可從 GC Roots 再繼續往下遍歷對象圖，這一步驟的停頓時間就必定會與 Java 堆容量直接成正比例關係了：堆越大，存儲的對象越多，對象圖結構越複雜，要標記更多對象而產生的停頓時間自然就更長。

要知道包含 “標記” 階段是所有追蹤式垃圾收集演算法的共同特征，如果這個階段會隨著堆變大而等比例增加停頓時間，其影響就會波及幾乎所有的垃圾收集器，同理可知，如果能夠削減這部分停頓時間的話，那收益也將會是系統性的。

想解決或者降低用戶線程的停頓，就要先搞清楚為什麼必須在一個能保障一致性的快照上才能進行對象圖的遍歷？為了能解釋清楚這個問題，我們引入三色標記（Tri-color Marking）作為工具來輔助推導，把遍歷對象圖過程中遇到的對象，按照 “是否訪問過” 這個條件標記成以下三種顏色：

• 白色：表示對象尚未被垃圾收集器訪問過。顯然在可達性分析剛剛開始的階段，所有的對象都是白色的，若在分析結束的階段，仍然是白色的對象，即代表不可達。
• 黑色：表示對象已經被垃圾收集器訪問過，且這個對象的所有引用都已經掃描過。黑色的對象代表已經掃描過，它是安全存活的，如果有其他對象引用指向了黑色對象，無須重新掃描一遍。黑色對象不可能直接（不經過灰色對象） 指向某個白色對象。
• 灰色：表示對象已經被垃圾收集器訪問過，但這個對象上至少存在一個引用還沒有被掃描過。

關於可達性分析的掃描過程，可以發揮一下想象力，把它看作對象圖上一股以灰色為波峰的波紋從黑向白推進的過程。如果用戶線程此時是凍結的，只有收集器線程在工作，那不會有任何問題。但如果用戶線程與收集器是併發工作呢？收集器在對象圖上標記顏色，同時用戶線程在修改引用關係（即修改對象圖的結構），這樣可能出現兩種後果。

• 一種是把原本消亡的對象錯誤標記為存活（即原本應該是白色的對象被誤標為黑色），這不是好事，但其實這種情況是可以容忍的，只不過產生了一點逃過本次收集的浮動垃圾而已，下次收集清理掉就好。
• 另一種是把原本存活的對象錯誤標記為已消亡（即原本應該是黑色的對象被誤標為白色），這就是非常致命的後果了，程式肯定會因此發生錯誤，下圖演示了這樣的致命錯誤具體是如何產生的。

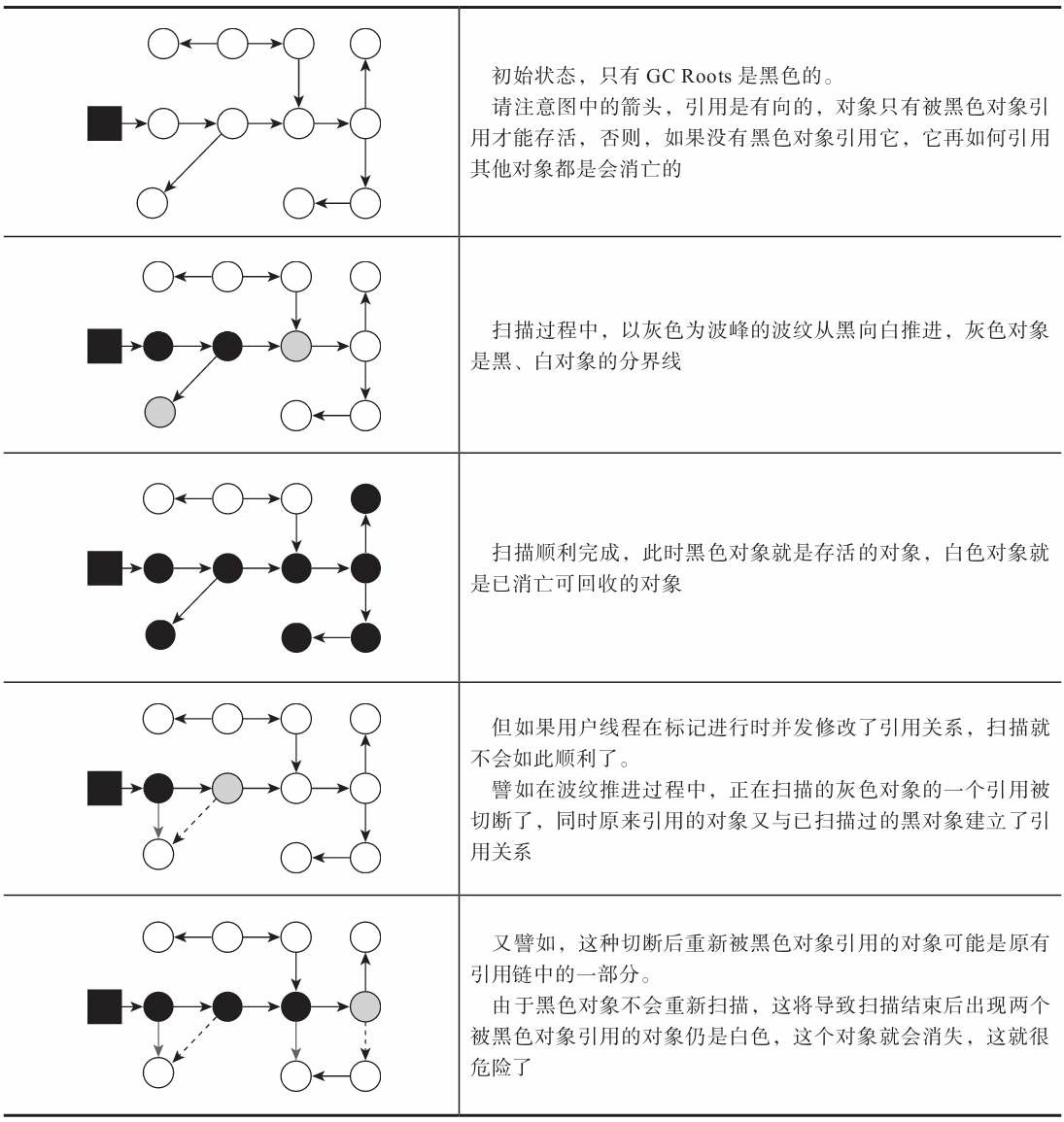
Wilson 於 1994 年在理論上證明瞭，當且僅當以下兩個條件同時滿足時，會產生 “對象消失” 的問題，即原本應該是黑色的對象被誤標為白色：

• 賦值器插入了一條或多條從黑色對象到白色對象的新引用；
• 賦值器刪除了全部從灰色對象到該白色對象的直接或間接引用。

因此，我們要解決併發掃描時的對象消失問題，只需破壞這兩個條件的任意一個即可。由此分別產生了兩種解決方案：增量更新（Incremental Update）和原始快照（Snapshot At The Beginning，SATB）。

• 增量更新要破壞的是第一個條件，當要插入黑色對象指向白色對象的引用關係時，就將這個新插入的引用記錄下來， 等併發掃描結束之後，再將這些記錄過的引用關係中的黑色對象為根，重新掃描一次。這可以簡化理解為，黑色對象一旦新插入了指向白色對象的引用之後，它就變回灰色對象了。
• 原始快照要破壞的是第二個條件，當要刪除灰色對象指向白色對象的引用關係時，就將這個要刪除的引用記錄下來， 等併發掃描結束之後，再將這些記錄過的引用關係中的灰色對象為根，重新掃描一次。這可以簡化理解為，無論引用關係刪除與否，都會按照剛剛開始掃描那一刻的對象圖快照來進行搜索。

以上無論是對引用關係記錄的插入還是刪除，虛擬機的記錄操作都是通過寫屏障實現的。

在 HotSpot 虛擬機中，增量更新和原始快照這兩種解決方案都有實際應用，譬如，CMS 是基於增量更新來做併發標記的，G1、Shenandoah 則是用原始快照來實現。

參考資料

《深入理解Java虛擬機》第 3 章：垃圾收集器與記憶體分配策略 3.4.6 併發的可達性分析

本文來自博客園，作者：真正的飛魚，轉載請註明原文鏈接：https://www.cnblogs.com/feiyu2/p/17305928.html