關於java的快速輸入的一點小bug

import java.io.*;

public class Main {
    public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static StreamTokenizer st = new StreamTokenizer(in);
    public static int nextInt() throws IOException {
        st.nextToken();
        return (int)st.nval;
    }
    public static long nextLong() throws IOException {
        st.nextToken();
        return (long)st.nval;
    }
    public static void main(String[] args) throws IOException {
        int n = nextInt();
        in.close();
        out.println(n);
        out.flush();
        out.close();
    }
}

 這個是java大佬們最常用的輸入方法了，但是在nextLong上有時會出現一些小小的bug，下麵的代碼是一個正常的StreamTokenizer的nextLong：

public static void main(String[] args) throws IOException {
        long x = nextLong();
        in.close();
        out.println(x);
        out.flush();
        out.close();
    }

輸入：1152921504606846976，這個數是在long的範圍內的(2^60)。看一下輸出結果。

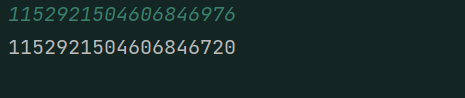
 出現這種現象的原因就是精度損失。

先看一看StreamTokenizer的nval()方法的返回

可以看出來，這個方法大概是把字元串轉化成double類型，而nextInt與nextLong方法則是把從字元串轉化而來的double型浮點數再轉化為long與int型整數。double型變數是64位，long也是64位，但是從浮點數的儲存原理來看這必然會出現精度損失的問題。

先來看看浮點數在電腦中的儲存方式。在我們的生活中，數的表示有兩種，一種是直接寫出它的值，另一種就是科學計數法了，比如1234567000000，是正常表示法，它也可也寫成科學計數法：1.23456*10¹²，當然，不可能保留太多位數的有效數字，不然的話科學計數法就失去了它的意義了，故一般寫成：1.23*10¹²。

在電腦中也有類似的表示方法，浮點數在計數機中就是通過這樣的方式存儲的。$$(-1)^{a}\times\beta\times2^{\vartheta}$$

α為符號位，表示浮點數整體的正負，β為尾碼，就相當於1.23*10¹²中的1.23，θ為階碼，用來表示指數的大小。在IEEE754標準中規定，64位浮點數的儲存格式為：

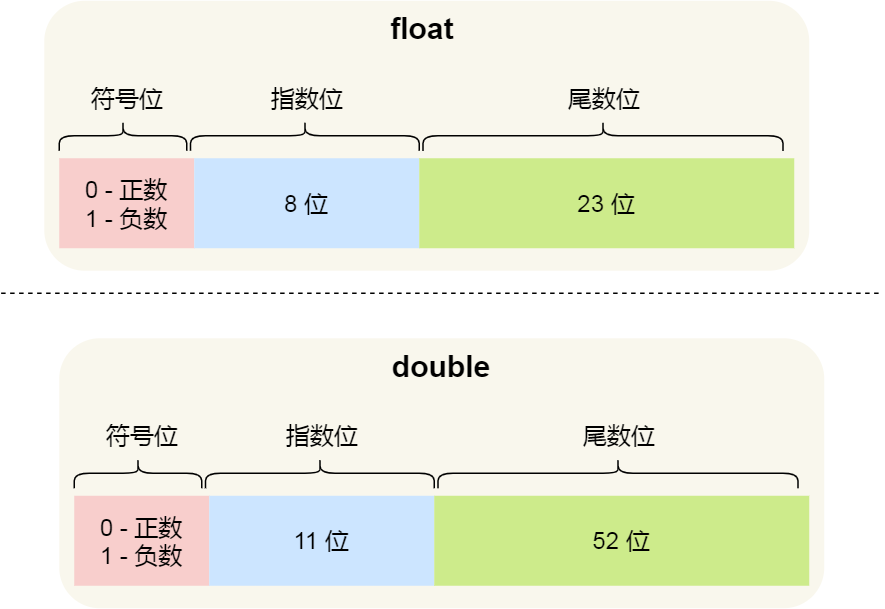
 最高位為符號位，大小為一位，階碼為11位，尾碼為52位。也就是說在double浮點數中，52位來表示1.23*10¹²中的1.23，而11位來表示指數，這相對於我們現實生活中的科學計數法友好得多，它有52位的有效位數不可，不容易損失精度。但是，long型整數可是有64位，double提供的有效位數相比起來不太夠看，這有的時候就會出現意想不到的bug，這也解釋了之前出現的那個bug，2^60 > 2^52。剛剛用十進位數舉的例子：1.23*10¹² == 1230000000000 相比它原來的大小1234567000000損失了不小。

為了進一步來驗證我的想法，來試著測試一下double轉long精度損失的臨界值，多輸入幾個值來測試：根據理論推測，在2^52之前應該都是準確沒有精度損失的，從2^52之後就會有精度損失，先來輸入(2^52) + 5 試試：

 結果出乎意料，竟然是準確的。後來才發現，是忘了一點：尾碼前面還有一位隱藏的1，正確的格式是：$$(-1)^{a}\times(1.\beta)\times2^{\vartheta}$$。所以一共是有53位都是用來表示尾碼的，那麼，推測一下，從2^53往後應該就會出現精度損失了：

先來測試一下2^53:

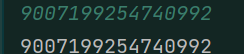
 2^53 + 1:

 果然，剛到2^53 + 1就出現了精度損失。

這就是使用StreamTokenizer的nval方法實現nextLong的時候可能出現的一點小bug，希望看到這篇文章的朋友以後在long的輸入的時候註意一下。本人是在打ACM校賽的時候遇到的這個問題，它時認為自己的代碼邏輯已經完美了，但是交上去之後全是wa加tle（單純就是卡java，1e6的數據，一個輸入加排序就超時了）

當時心態就有點炸。最後也沒打好，回來之後調試也沒有發現哪不對，直到我把那接近10的18次方的大數單獨輸入了一遍才發現了問題。希望大家能避開這個坑。

另外關於nextLong，本人也沒有非常好的處理方法，在n<2^53的時候完全可以直接用nval轉long，但超過這個值就不要用這個方法了，目前，我只知道兩個方法：

一個用StringTokenizer讀入一個字元串，然後直接pase字元串成long值：

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
    public static StringTokenizer st = new StringTokenizer("");
    public static String next() throws IOException {
        while(!st.hasMoreTokens()) {
            st = new StringTokenizer(in.readLine());
        }
        return st.nextToken();
    }
    public static long nextLong() throws IOException {
        return Long.parseLong(next());
    }
    public static void main(String[] args) throws IOException {
        long x = nextLong();
        in.close();
        out.println(x);
        out.flush();
        out.close();
    }
}

輸入2^60

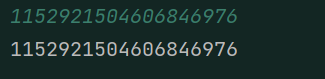
 另一種類似於c++的快讀，但是java沒法自己調用寄存器（以我的認知，大佬可能有辦法）也沒有inline，所以達不到快讀的效果，但是比Scanner肯定是要快的，甚至，通過學校的oj的結果來看，比上一種方法還快：

import java.io.*;
import java.util.StringTokenizer;

public class Main {
    public static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
    public static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));

    public static long nextLong() throws IOException {
        long res = 0;
        boolean f = true;
        int c = 0;
        while(c < 48 || c > 57) {
            if(c == '-')
                f = false;
            c = in.read();
        }
        while(c >= 48 && c <= 57) {
            res = (res<<3) + (res<<1) + c - 48;
            c = in.read();
        }
        return f ? res : -res;
    }
    public static void main(String[] args) throws IOException {
        long x = nextLong();
        in.close();
        out.println(x);
        out.flush();
        out.close();
    }
}

總結，通過StreamTokenizer的nval方法實現nextLong的時候，當數值大於2^53的時候就會出現精度損失，從而出現難以意料的bug，應對方法，就是上面提到的兩種1、通過StringTokenizer，直接把字元串轉化為long。2、借鑒c++,低配版快讀。但是這兩種方法均比StreamTokenizer的nval轉long慢，所以在2^53之前還是建議用StreamTokenizer。如果有更好的方案，歡迎大佬來指教。