代碼優化與程式加速指南——針對數值優化和深度學習領域

来源:https://www.cnblogs.com/sashabanks/archive/2023/03/06/17184208.html
-Advertisement-
Play Games

背景 當需要處理規模較大、任務較複雜的優化問題或訓練神經網路時，我們經常會遇到程式運行時間長或無法完成的情況。然而，這不一定是由於問題規模大或電腦硬體能力的限制。即使嘗試使用更高性能的伺服器或電腦，也不能保證能夠有效地加速代碼運行。因為高性能的硬體通常需要與為高性能計算而設計的代碼相匹配。 本文 ...


背景

當需要處理規模較大、任務較複雜的優化問題或訓練神經網路時，我們經常會遇到程式運行時間長或無法完成的情況。然而，這不一定是由於問題規模大或電腦硬體能力的限制。即使嘗試使用更高性能的伺服器或電腦，也不能保證能夠有效地加速代碼運行。因為高性能的硬體通常需要與為高性能計算而設計的代碼相匹配。

本文旨在為程式加速提供一些代碼方面的優化思路，通過優化代碼結構、設計高性能計算方案，來有效加速程式運行，提高程式運行效率。需要註意的是，本文只涉及代碼層面的加速方案，不包括演算法、硬體等方面的優化措施。文章的撰寫基於個人經驗，如果有不足之處，敬請指出。

本文將介紹一些常見的代碼優化技巧，例如使用向量化和並行化的方式來加速計算、減少記憶體的占用以及利用編譯器優化代碼的迴圈結構等。
主要思路

代碼優化

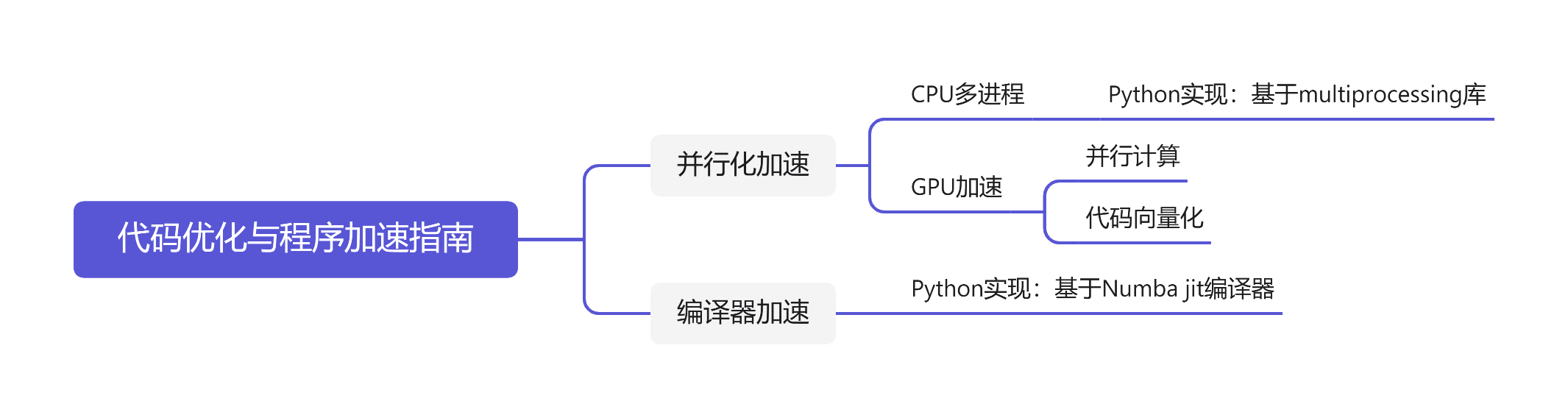
簡單來說，實現程式優化的方式主要有兩種思路。一種是並行化任務，編寫並行化代碼，以利用多核CPU或GPU的並行計算能力來加速程式運行。另一種則是利用編譯器的代碼優化機制，將Python、MATLAB等需要解釋器執行的代碼部分編譯成機器代碼，以實現更快的程式運行速度。

1 並行化

程式優化的另一種思路是通過並行化加速程式。並行化需要軟體與硬體配合，但前提是總任務能夠被分解為同時進行的子任務。並行化有兩種方式，一種依靠多核CPU實現多進程操作，一種依靠GPU完成。下麵我們將分別介紹這兩種方式的實現方法。

1.1 CPU多進程操作

多進程操作是利用CPU多核心的特性來實現並行化計算。在多進程操作中，程式將被分解成多個子任務，每個子任務都在獨立的進程中運行。這些進程可以並行地執行不同的任務，從而加速程式的運行。多進程操作可以使用Python的multi-processing庫來實現。

1.1.1 多進程

當我們在電腦上運行程式時，實際上是啟動了一個進程。進程是指在操作系統中運行的一個程式，它占據著系統的一些資源，如記憶體、CPU時間等。在傳統的單進程計算模型中，所有的任務都在同一個進程中執行，如果任務需要進行複雜的計算，就會耗費大量時間，且無法利用多核CPU的優勢。而多進程技術可以將任務分解為多個子任務，每個子任務在一個獨立的進程中執行，從而實現並行計算，提高了計算效率。

1.1.2 多進程的Python實現

在使用multi-processing庫進行多進程操作時，首先需要將任務分解成多個子任務，並將每個子任務交給不同的進程來執行。

這是multiprocessing庫的代碼框架

import multiprocessing

def worker(num):
    """子進程要執行的任務"""
    print(f"Worker {num} is running")
    return

if __name__ == "__main__":
    processes = []
    num_processes = 4

    # 創建多個子進程
    for i in range(num_processes):
        p = multiprocessing.Process(target=worker, args=(i,))
        processes.append(p)
        p.start()

    # 等待所有子進程完成
    for p in processes:
        p.join()

    print("All workers are done")

在這個例子中，我們首先定義了一個worker函數，它是每個子進程要執行的任務。然後在主進程（if name=="main"）中，我們創建了num_processes個子進程，並將它們添加到processes列表中。接著，我們遍歷processes列表，用Process類中的start()方法啟動每個子進程，並等待它們完成。最後輸出"All workers are done"，表示所有子進程都已經執行完畢。

這個示例代碼只是一個簡單的例子，實際應用中，我們可以根據具體情況編寫更複雜的子進程任務函數，並使用multiprocessing庫中提供的各種工具實現更複雜的多進程操作。

1.2 GPU

相比於CPU，GPU有著更多的計算核心和更高的計算能力，可以更好地支持並行化計算。因此，利用GPU進行代碼優化可以大幅度提高程式的運行效率。而要在Python中使用GPU進行代碼優化，則需要使用GPU編程框架，比較常見的有NVIDIA開發的CUDA框架以及OpenCL框架。

1.2.1 GPU並行計算的Python實現

其中，CUDA是由NVIDIA推出的GPU編程框架，它可以讓開發者利用GPU的並行計算能力，加速各種計算密集型任務。CUDA提供了一組API，可以方便地進行GPU的編程，支持C/C++、Python、Java等多種編程語言。在使用CUDA時，需要使用CUDA工具包，其中包括CUDA驅動程式、CUDA運行時庫和CUDA工具。

以下是一個簡單的利用CUDA框架實現向量加法的例子：

import numpy as np
from numba import cuda

# 定義向量加法函數
@cuda.jit
def vector_add(a, b, c):
    i = cuda.grid(1)
    if i < len(c):
        c[i] = a[i] + b[i]

# 定義主程式
if __name__ == '__main__':
    # 定義向量大小
    n = 100000

    # 在主機上生成隨機向量
    a = np.random.randn(n).astype(np.float32)
    b = np.random.randn(n).astype(np.float32)
    c = np.zeros(n, dtype=np.float32)

    # 將數據傳輸到GPU顯存中
    d_a = cuda.to_device(a)
    d_b = cuda.to_device(b)
    d_c = cuda.to_device(c)

    # 定義線程塊和線程數量
    threads_per_block = 64
    blocks_per_grid = (n + (threads_per_block - 1)) // threads_per_block

    # 執行向量加法操作
    vector_add[blocks_per_grid, threads_per_block](d_a, d_b, d_c)

    # 將結果從GPU顯存中傳輸回主機記憶體
    d_c.copy_to_host(c)

    # 列印結果
    print(c)

在上述代碼中，我們首先定義了一個vector_add函數，用於將兩個向量相加並將結果存儲在第三個向量中。然後我們生成了兩個隨機向量，並將其傳輸到GPU顯存中。接著，我們定義了線程塊和線程數量，併在GPU部分，我們需要註意的是代碼的向量化，也就是多利用矩陣運算編寫代碼，而不是多重for loop的串列計算。這樣可以充分利用GPU的並行計算能力，加速神經網路的訓練過程。例如，可以使用cuBLAS庫來實現矩陣乘法，使用cuDNN庫來實現捲積操作等。執行了向量加法操作。最後，我們將結果從GPU顯存中傳輸回主機記憶體，並列印出結果。

值得註意的是，由於CUDA框架需要GPU的支持，因此我們在使用CUDA框架時需要保證系統中有可用的GPU。

1.2.2利用GPU訓練神經網路

當涉及到訓練深度神經網路時，GPU可以發揮其優勢，因為神經網路的訓練往往需要進行大量的矩陣運算，這正是GPU擅長的任務。為了使用GPU進行深度神經網路的訓練，需要利用一些特定的框架和庫，比如TensorFlow和PyTorch。
在利用CUDA框架進行神經網路訓練時，首先，需要定義一個在GPU上運行的張量（tensor）來存儲神經網路的參數。然後，將數據載入到GPU記憶體中，並將計算任務分配到GPU核心上。
下麵是一個簡單的基於PyTorch和CUDA的神經網路訓練代碼示例：

import torch
import torch.nn as nn
import torch.optim as optim

# 定義神經網路模型
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(3, 6, 5)
        self.pool = nn.MaxPool2d(2, 2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = self.pool(F.relu(self.conv1(x)))
        x = self.pool(F.relu(self.conv2(x)))
        x = x.view(-1, 16 * 5 * 5)
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

# 定義訓練數據和標簽
inputs = torch.randn(1, 3, 32, 32)
labels = torch.randn(1, 10)

# 將神經網路模型移動到GPU上
net = Net().cuda()

# 將訓練數據和標簽移動到GPU上
inputs = inputs.cuda()
labels = labels.cuda()

# 定義損失函數和優化器
criterion = nn.MSELoss()
optimizer = optim.SGD(net.parameters(), lr=0.01)

# 開始訓練
for epoch in range(100):
    optimizer.zero_grad()
    outputs = net(inputs)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()
    print('Epoch %d, Loss: %.4f' % (epoch+1, loss.item()))

在上面的代碼中，我們通過xxx.cuda()的方法將模型、訓練數據和標簽都載入到GPU記憶體中，從而使得訓練迴圈中涉及的運算全部在GPU上完成。

1.2.3 註意事項

值得特別註意的是，如果要利用GPU實現加速，那麼一定要保證代碼的向量化。簡單來說，就是儘可能用矩陣運算的方式來表示數值計算過程，而不是用多重for loop的形式。

這是因為，GPU相較於CPU只是強在並行上，但是計算能力是差於CPU的，多層for迴圈這樣的串列計算並不適合GPU。用沐神的話說，如果把CPU比作是一個大學生的話，GPU就像是一群小學生。大學生可以做微積分這樣的任務，小學生只能做加減乘除。但如果把一個微積分這樣的任務分解成多個加減乘除，那麼一群小學生這樣的GPU的優勢就體現出來了。

舉一個簡單的例子，例如我們要設計一個這樣的損失函數：

\[L_\theta=-\sum_{i=1}^{N}\sum_{j=1}^{N_i}w_{ij}log(p(x_i^j|M)) \]

如果沒有刻意註意代碼的向量化，那麼很容易想到的思路是這樣的：

	def lossFunc(y_pred,sols,objs):
	batch size=y_pred.shape[0]
	loss=torch.tensor(0.0)
	for i in range(batch_size):
		nSols=sols[i].shape[0] #當前batch(MIP)下的可行解數目
		nVars=sols[i].shape[1]
		#目標斷數歸-化
		den=objs[i].sum()
		for l in range(objs[i].shape[0]):
			objs[i][l]=objs[i][l]/den
		den=sum(exp(-objs[i]))#計算wii繫數的分母
		sum1=torch.tensor(0.0)
		for j in range(nSols):
			#計算權重wij
			w=exp(-objs[il[j])/den
			#計算可行解生成的概率
			P=torch.tensor(1.9)
			for k in range(nVars):
				if sols[il[j,k]==1:
					P=p*y_pred[i][k]
				elif sols[il[j,k]==0:
					P=p*(1-y_pred[i][k])
			#計算求和
			sum1+=w*p
		loss+=sum1
	loss=-loss
	return loss

但實際上用多重for迴圈設計的損失函數並不利於在GPU上工作，甚至比不上在CPU上執行這樣的代碼。最後測試結果發現如果使用這樣的損失函數，一個epoch大約跑1個小時....所以也不可能把神經網路訓練出來了。

def lossFunc(y,sols,objs):
    """
    損失函數
    Parameters
    ----------
    y : 神經網路輸出 batch_size x nVars
    sols : 可行解集合 batch_size x nSols x nVars
    objs : 可行解對應的目標函數值 batch_size x nSols

    Returns
    -------
    loss : 在當前batch上的損失
    """
    objs=objs/15
    eObjs=exp(-objs)
    den=eObjs.sum(axis=1)
    den=den.unsqueeze(1)
    w=eObjs/den
    y=y.unsqueeze(1)
    p=y*sols+(1-y)*(1-sols)
    p=log(p+1e-45)
    P=p.sum(axis=2)
    loss=-(w*P).sum()
    return loss

所以正確的寫法應該是這樣的，不僅在GPU上加速效果明顯，並且看起來簡潔多了...但是缺點就是，得不斷利用矩陣運算的廣播機制，並且最好在小規模的例子上多手算幾遍，邊算邊設計。

2 編譯器加速

2.1 原理

在電腦編程中，編譯型語言和解釋型語言是兩種常見的語言類型。與解釋型語言相比，編譯型語言由於在執行之前需要先將代碼編譯成可執行的二進位代碼，所以執行速度更快。這是因為編譯器能夠將源代碼優化為更高效的機器代碼，從而加快程式的執行速度。

編譯器優化的方式有很多種，其中最常見的方式包括：

  1. 消除不必要的計算：編譯器可以在編譯代碼時識別出不必要的計算，從而避免浪費計算資源。

  2. 迴圈展開：迴圈展開是指將迴圈體中的代碼重覆執行幾次，從而減少迴圈的次數。這樣可以提高程式的運行速度。

  3. 矩陣/向量化：矩陣/向量化是指將多個數據放入矩陣或向量中，然後一次性進行計算。這種方式可以減少迴圈的次數，從而提高程式的運行速度。

為了幫助開發者更加方便地利用編譯器優化代碼，一些開源JIT編譯器如Numba被開發出來。這些編譯器可以將Python等解釋型語言代碼轉換為可執行的機器代碼，從而提高程式的運行速度。

2.2 基於Numba的Python加速方案

Numba是一種基於LLVM編譯器的開源JIT編譯器，可以將Python代碼轉換為機器代碼，從而實現代碼加速。Numba支持多種優化技術，包括迴圈展開、代碼向量化等。使用Numba可以極大地提高Python代碼的執行速度。

下麵是一個使用Numba實現代碼加速的大致代碼框架：

  1. 導入numba庫
  2. 定義一個需要優化的函數
  3. 使用 @numba.jit 裝飾器對函數進行裝飾，生成numba優化後的函數
  4. 調用優化後的函數

下麵以一個對比案例為例，來說明如何使用Numba實現Python代碼加速。
假設我們有一個多重嵌套的for迴圈，用於計算一個矩陣的行列式。這是一個非常計算密集的操作，可以使用Numba進行加速。

原始Python代碼：

def det(matrix):
    n = len(matrix)
    if n == 1:
        return matrix[0][0]
    elif n == 2:
        return matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0]
    else:
        result = 0
        for j in range(n):
            sub_matrix = []
            for i in range(1, n):
                row = []
                for k in range(n):
                    if k != j:
                        row.append(matrix[i][k])
                sub_matrix.append(row)
            result += matrix[0][j] * det(sub_matrix) * (-1) ** j
        return result

可以看到，這個函數包含了多重嵌套的for迴圈，非常容易受到Python解釋器的性能限制。現在我們使用Numba進行加速。

優化後的Numba代碼：

import numba

@numba.jit(nopython=True)
def det(matrix):
    n = len(matrix)
    if n == 1:
        return matrix[0][0]
    elif n == 2:
        return matrix[0][0] * matrix[1][1] - matrix[0][1] * matrix[1][0]
    else:
        result = 0
        for j in range(n):
            sub_matrix = np.zeros((n-1, n-1))
            for i in range(1, n):
                for k in range(n):
                    if k != j:
                        sub_matrix[i-1, k-(k>j)] = matrix[i, k]
            result += matrix[0][j] * det(sub_matrix) * (-1) ** j
        return result

我們使用了@numba.jit(nopython=True)裝飾器，將函數聲明為Numba可加速的函數。同時，我們使用了Numpy數組代替了Python的列表，並使用Numpy數組的切片操作和廣播功能，以減少迴圈和記憶體分配。

測試代碼：

import time
import numpy as np

# Generate a random 10x10 matrix
matrix = np.random.rand(10, 10)

# Time the original Python code
start = time.time()
d = det(matrix)
end = time.time()
print(f"Python code took {end-start:.4f} seconds, result={d}")

# Time the Numba-optimized code
start = time.time()
d = det(matrix)
end = time.time()
print(f"Numba-optimized code took {end-start:.4f} seconds, result={d}")

測試結果：

Python code took 0.5960 seconds, result=-0.004127521725273144
Numba-optimized code took 0.0040 seconds, result=-0.004127521725273144

使用Numba優化Python代碼的大致流程如上所述。對於需要優化的函數，我們可以通過添加numba.jit 裝飾器實現代碼優化，該裝飾器會自動進行類型推導並將Python代碼編譯為機器碼。

需要註意的是，Numba並不是萬能的，它能夠加速的代碼類型是有一定限制的。例如，迴圈嵌套過深的代碼可能不適合使用Numba進行優化。因此，在使用Numba時，需要仔細評估代碼的結構和類型，以確定是否適合使用Numba進行優化。

此外，還需要註意的是，Numba在進行代碼優化時，會將Python代碼轉換為LLVM IR（Intermediate Representation，中間表示形式），這一過程可能會導致代碼的可讀性降低。因此，在使用Numba進行優化時，需要仔細考慮代碼可讀性和可維護性的平衡。

總結

在這篇技術博客中，我們介紹了幾種常見的代碼優化技術，包括並行計算、編譯器優化等。這些技術可以在不改變程式邏輯的前提下，提高代碼的運行效率和性能。其中，我們通過對比並行計算與串列計算的運行效率差異，詳細講解瞭如何利用GPU加速神經網路訓練。此外，我們還介紹了編譯型語言比解釋型語言執行快的原因，以及編譯器如何優化代碼實現加速的原理。最後，我們著重介紹了一個開源的JIT編譯器Numba，並通過一個實際案例演示瞭如何利用Numba優化多重嵌套for迴圈的Python代碼。

值得一提的是，這篇技術博客是在chatGPT的幫助下共同完成的。作者提供了大致的寫作思路和要點，而主要內容和其中的代碼案例均由chatGPT構建。我們相信，本篇博客對於想要提高代碼性能和效率的程式員們會有所幫助。


附圖





您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • SICP：賦值和局部狀態（Python實現）
    前面我們介紹了組成程式的各種基本元素，看到瞭如何把基本過程和基本數據組合起來，構造出複合的實體。不過對於設計程式而言，這些手段還不夠，我們還需要一些能夠幫助我們構造起模塊化（modular）的大型系統的策略。所謂模塊化，也即使這些系統能夠“自然地”劃分為一些內聚（coherent）的部分，使這些部分... ...
  • Qt 學習筆記 - 第二章 - 添加圖片、佈局、界面切換
    Qt 學習筆記全系列傳送門： Qt 學習筆記 - 第一章 - 快速開始、信號與槽 【本章】Qt 學習筆記 - 第二章 - 添加圖片、佈局、界面切換 1、給 Qt 工程添加圖片 註意：不要隨意更改所需圖片的尾碼，否則可能導致無法正常使用，出現*Image format not supported*文件 ...
  • 07字元串操作
    字元串（str） 字元串的下標（索引） str_data = "python" p y t h o n 0 1 2 3 4 5 -6 -5 -4 -3 -2 -1 索引就是某數據在序列的位置 正索引：從左至右，從0開始 負索引：從右至左，從-1開始 其中：str_data[0] = str_data ...
  • 函數編程：強大的 Stream API
    函數編程：強大的 Stream API 每博一文案 只要有人的地方，世界就不會是冰冷的，我們可以平凡，但絕對不可以平庸。 —————— 《平凡的世界》 人活著，就得隨時準備經受磨難。他已經看過一些書，知道不論是普通人還是了不起的人， 都要在自己的一生中經歷許多磨難。磨難使人堅強。 —————— 《平 ...
  • 統一日誌輸出列印POST請求參數
    眾所周知，request.getInputStream()只能調一次。如果希望在請求進入Controller之前統一列印請求參數（攔截器或過濾器），又不影響業務，我們只能將獲取到的輸入流緩存起來，後續都從緩存中獲取即可。 首先，自定義一個ServletInputStream package com. ...
  • 如何使用JDBC將Cordova應用程式連接到MySQL資料庫？
    不建議使用JDBC直接將您的Cordova應用程式連接到MySQL資料庫，因為它會帶來安全風險.移動設備通常受到安全漏洞的約束，並且從移動應用程式連接到資料庫會增加暴露敏感信息的風險. 一種更好的方法是使用Back-最終服務(例如REST API)與資料庫進行交互.您的Cordova應用程式將與RE ...
  • 【Java】先return還是先finally
    函數式編程：Lambda 表達式 每博一文案 曾經讀過的依然令我感動的句子，生活總是不如意，但往往是在無數痛苦中，但往往是在無數痛苦中，在重重矛盾 和艱難中才能成熟起來，堅強起來，愛情啊，它使荒蕪變成繁榮，平庸變得偉大，使死去的複活，活著的閃閃發光， 即使愛情是不盡的煎熬折磨，像冰霜般嚴厲，烈火般烤 ...
  • java對接SCOM微軟監控系統告警
    背景 項目上需要對接scom微軟監控系統告警，能夠拿到手的資料十分有限，只有幾個官方文檔地址： Operations Manager REST API Reference - Operations Manager REST API | Microsoft Learn SCOM: Quick Star ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類