1. 引言 在實際的項目中,樹還是用的比較多的一種,尤其是對於具有層次結構的數據。相信很多人都學過樹的遍歷,比如先序遍歷,後序遍歷等,利用遞歸還是很容易理解的。 今天給大家介紹下二叉樹的幾種遍歷演算法,包括遞歸和非遞歸的實現。 首先建立一棵二叉樹 如: 一棵簡單的二叉樹 2. 先序遍歷 先序遍歷還是很 ...
1. 引言
在實際的項目中,樹還是用的比較多的一種,尤其是對於具有層次結構的數據。相信很多人都學過樹的遍歷,比如先序遍歷,後序遍歷等,利用遞歸還是很容易理解的。
今天給大家介紹下二叉樹的幾種遍歷演算法,包括遞歸和非遞歸的實現。
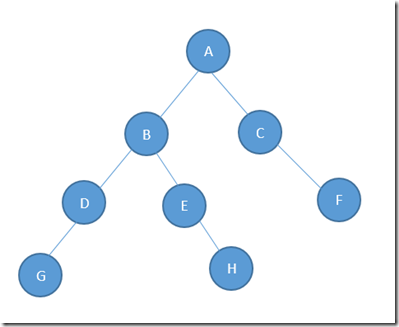
首先建立一棵二叉樹 如:
[DebuggerDisplay("Value={Value}")] public class Tree { public string Value; public Tree Left; public Tree Right; } public static Tree CreatFakeTree() { Tree tree = new Tree() {Value = "A"}; tree.Left = new Tree() { Value = "B", Left = new Tree() {Value = "D", Left = new Tree() {Value = "G"}}, Right = new Tree() {Value = "E", Right = new Tree() {Value = "H"}} }; tree.Right = new Tree() {Value = "C", Right = new Tree() {Value = "F"}}; return tree; }
一棵簡單的二叉樹
2. 先序遍歷
先序遍歷還是很好理解的,一次遍歷根節點,左子樹,右子數
遞歸實現
public static void PreOrder(Tree tree) { if (tree == null) return; System.Console.WriteLine(tree.Value); PreOrder(tree.Left); PreOrder(tree.Right); }
非遞歸實現
public static void PreOrderNoRecursion(Tree tree) { if(tree == null) return; System.Collections.Generic.Stack<Tree> stack = new System.Collections.Generic.Stack<Tree>(); Tree node = tree; while (node != null || stack.Any()) { if (node != null) { stack.Push(node); System.Console.WriteLine(node.Value); node = node.Left; } else { var item = stack.Pop(); node = item.Right; } } }
3. 中序遍歷
遞歸實現
public static void InOrder(Tree tree) { if(tree == null) return; InOrder(tree.Left); System.Console.WriteLine(tree.Value); InOrder(tree.Right); }
非遞歸實現
public static void InOrderNoRecursion(Tree tree) { if (tree == null) return; System.Collections.Generic.Stack<Tree> stack = new System.Collections.Generic.Stack<Tree>(); Tree node = tree; while (node != null || stack.Any()) { if (node != null) { stack.Push(node); node = node.Left; } else { var item = stack.Pop(); System.Console.WriteLine(item.Value); node = item.Right; } } }
4. 後序遍歷
遞歸實現
public static void PostOrder(Tree tree) { if (tree == null) return; PostOrder(tree.Left); PostOrder(tree.Right); System.Console.WriteLine(tree.Value); }
非遞歸實現 比前兩種稍微複雜一點。要保證左右節點都被訪問後,才能訪問根節點。這裡給出兩種形式。
public static void PostOrderNoRecursion(Tree tree) { if (tree == null) return; System.Collections.Generic.Stack<Tree> stack = new System.Collections.Generic.Stack<Tree>(); Tree node = tree; Tree pre = null; stack.Push(node); while (stack.Any()) { node = stack.Peek(); if ((node.Left == null && node.Right == null) || (pre != null && (pre == node.Left || pre == node.Right))) { System.Console.WriteLine(node.Value); pre = node; stack.Pop(); } else { if(node.Right != null) stack.Push(node.Right); if(node.Left != null) stack.Push(node.Left); } } } public static void PostOrderNoRecursion2(Tree tree) { HashSet<Tree> visited = new HashSet<Tree>(); System.Collections.Generic.Stack<Tree> stack = new System.Collections.Generic.Stack<Tree>(); Tree node = tree; while (node != null || stack.Any()) { if (node != null) { stack.Push(node); node = node.Left; } else { var item = stack.Peek(); if (item.Right != null && !visited.Contains(item.Right)) { node = item.Right; } else { System.Console.WriteLine(item.Value); visited.Add(item); stack.Pop(); } } } }
5. 層序遍歷
層序遍歷就是按照層次由左向右輸出
public static void LevelOrder(Tree tree) { if(tree == null) return; Queue<Tree> queue = new Queue<Tree>(); queue.Enqueue(tree); while (queue.Any()) { var item = queue.Dequeue(); System.Console.Write(item.Value); if (item.Left != null) { queue.Enqueue(item.Left); } if (item.Right != null) { queue.Enqueue(item.Right); } } }
6. Z-型層序遍歷
Z-層序遍歷就是奇數層按照由左向右輸出,偶數層按照由右向左輸出,這裡定義了幾個輔助函數,比如計算節點所在的層次。演算法思想是按照層次保存樹形節點,應該是有更加優化的演算法,希望大家指出。
public static int GetDepth(Tree tree, Tree node) { if (tree == null) return 0; if (tree == node) return 1; if (tree.Left == node || tree.Right == node) return 2; int lDepth = GetDepth(tree.Left, node); lDepth = lDepth == 0 ? 0 : lDepth + 1; int rDepth = GetDepth(tree.Right, node); rDepth = rDepth == 0 ? 0 : rDepth + 1; return lDepth >= rDepth ? lDepth : rDepth; } public static void Z_LevelOrder(Tree tree, Dictionary<int, List<Tree>> dictionary) { if (tree == null) return; Queue<Tree> queue = new Queue<Tree>(); queue.Enqueue(tree); while (queue.Any()) { var item = queue.Dequeue(); var depth = GetDepth(tree, item); List<Tree> list; if (!dictionary.TryGetValue(depth, out list)) { list = new List<Tree>(); dictionary.Add(depth, list); } list.Add(item); if (item.Left != null) { queue.Enqueue(item.Left); } if (item.Right != null) { queue.Enqueue(item.Right); } } } public static void Z_LevelOrder(Tree tree) { if (tree == null) return; Dictionary<int, List<Tree>> dictionary = new Dictionary<int, List<Tree>>(); Z_LevelOrder(tree, dictionary); foreach (KeyValuePair<int, List<Tree>> pair in dictionary) { if (pair.Key%2 == 0) { pair.Value.Reverse(); } pair.Value.ForEach(t=> { System.Console.Write(t.Value); }); } }