基於sklearn的集成學習實戰_ZenDei技術網路在線

本文主要跟隨Datawhale的學習路線以及內容教程，詳細介紹了集成學習常見的多個演算法的基於sklearn的實現過程，同時還有兩個案例，內容豐富。 ...

集成學習投票法與bagging

投票法

sklearn提供了VotingRegressor和VotingClassifier兩個投票方法。使用模型需要提供一個模型的列表，列表中每個模型採用tuple的結構表示，第一個元素代表名稱，第二個元素代表模型，需要保證每個模型擁有唯一的名稱。看下麵的例子：

from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifier
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

models = [('lr',LogisticRegression()),('svm',SVC())]
ensemble = VotingClassifier(estimators=models)  # 硬投票

models = [('lr',LogisticRegression()),('svm',make_pipeline(StandardScaler(),SVC()))]
ensemble = VotingClassifier(estimators=models,voting='soft')  # 軟投票

我們可以通過一個例子來判斷集成對模型的提升效果。

首先我們創建一個1000個樣本，20個特征的隨機數據集合：

from sklearn.datasets import make_classification
def get_dataset():
    X, y = make_classification(n_samples = 1000, # 樣本數目為1000
                              n_features = 20,  # 樣本特征總數為20
                              n_informative = 15,  # 含有信息量的特征為15
                              n_redundant = 5, # 冗餘特征為5
                              random_state = 2)
    return X, y

補充一下函數make_classification的參數：

n_samples：樣本數量，預設100
n_features：特征總數，預設20
n_imformative：信息特征的數量
n_redundant：冗餘特征的數量，是信息特征的隨機線性組合生成的
n_repeated：從信息特征和冗餘特征中隨機抽取的重覆特征的數量
n_classes：分類數目
n_clusters_per_class：每個類的集群數
random_state：隨機種子

使用KNN模型來作為基模型：

def get_voting():
    models = list()
    models.append(('knn1', KNeighborsClassifier(n_neighbors=1)))
    models.append(('knn3', KNeighborsClassifier(n_neighbors=3)))
    models.append(('knn5', KNeighborsClassifier(n_neighbors=5)))
    models.append(('knn7', KNeighborsClassifier(n_neighbors=7)))
    models.append(('knn9', KNeighborsClassifier(n_neighbors=9)))
    ensemble = VotingClassifier(estimators=models, voting='hard')
    return ensemble

為了顯示每次模型的提升，加入下麵的函數：

def get_models():
    models = dict()
    models['knn1'] = KNeighborsClassifier(n_neighbors=1)
    models['knn3'] = KNeighborsClassifier(n_neighbors=3)
    models['knn5'] = KNeighborsClassifier(n_neighbors=5)
    models['knn7'] = KNeighborsClassifier(n_neighbors=7)
    models['knn9'] = KNeighborsClassifier(n_neighbors=9)
    models['hard_voting'] = get_voting()
    return models

接下來定義下麵的函數來以分層10倍交叉驗證3次重覆的分數列表的形式返回：

from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
def evaluate_model(model, X, y):
    cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state = 1)
    # 多次分層隨機打亂的K折交叉驗證
    scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1,
                            error_score='raise')
    return scores

接著來總體調用一下：

from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
X, y = get_dataset()
models = get_models()
results, names = list(), list()

for name, model in models.items():
    score = evaluate_model(model,X, y)
    results.append(score)
    names.append(name)
    print("%s %.3f  (%.3f)" % (name, score.mean(), score.std()))
    
plt.boxplot(results, labels = names, showmeans = True)
plt.show()

knn1 0.873  (0.030)
knn3 0.889  (0.038)
knn5 0.895  (0.031)
knn7 0.899  (0.035)
knn9 0.900  (0.033)
hard_voting 0.902  (0.034)

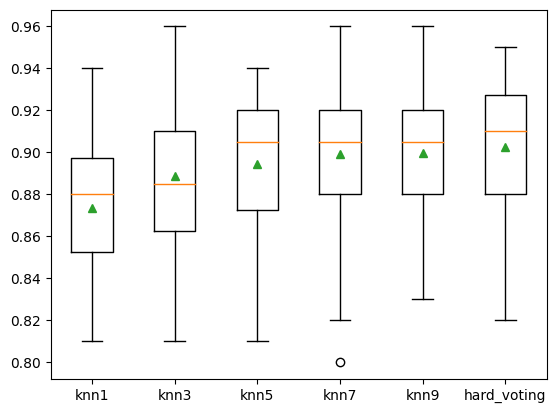
KNN提升箱型圖

可以看到結果不斷在提升。

bagging

同樣，我們生成數據集後採用簡單的例子來介紹bagging對應函數的用法：

from numpy import mean
from numpy import std
from sklearn.datasets import make_classification
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import RepeatedStratifiedKFold
from sklearn.ensemble import BaggingClassifier

X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=5)
model = BaggingClassifier()
cv = RepeatedStratifiedKFold(n_splits=10, n_repeats=3, random_state=1)
n_scores = cross_val_score(model, X, y, scoring='accuracy', cv=cv, n_jobs=-1, error_score='raise')
print('Accuracy: %.3f (%.3f)' % (mean(n_scores), std(n_scores)))

Accuracy: 0.861 (0.042)

Boosting

關於這方面的理論知識的介紹可以看我這篇博客。

這邊繼續關註這方面的代碼怎麼使用。

Adaboost

先導入各種包：

import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt
plt.style.use("ggplot")
%matplotlib inline
import seaborn as sns

# 載入訓練數據：         
wine = pd.read_csv("https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data",header=None)
wine.columns = ['Class label', 'Alcohol', 'Malic acid', 'Ash', 'Alcalinity of ash','Magnesium', 'Total phenols','Flavanoids', 'Nonflavanoid phenols', 
                'Proanthocyanins','Color intensity', 'Hue','OD280/OD315 of diluted wines','Proline']

# 數據查看：
print("Class labels",np.unique(wine["Class label"]))
wine.head()

Class labels [1 2 3]

那麼接下來就需要對數據進行預處理：

# 數據預處理
# 僅僅考慮2，3類葡萄酒，去除1類
wine = wine[wine['Class label'] != 1]
y = wine['Class label'].values
X = wine[['Alcohol','OD280/OD315 of diluted wines']].values

# 將分類標簽變成二進位編碼：
from sklearn.preprocessing import LabelEncoder
le = LabelEncoder()
y = le.fit_transform(y)

# 按8：2分割訓練集和測試集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,random_state=1,stratify=y)  # stratify參數代表了按照y的類別等比例抽樣

這裡補充一下LabelEncoder的用法，官方給出的最簡潔的解釋為：

Encode labels with value between 0 and n_classes-1.

也就是可以將原來的標簽約束到[0,n_classes-1]之間，1個數字代表一個類別。其具體的方法為：

fit、transform：

le = LabelEncoder()
le = le.fit(['A','B','C'])  # 使用le去擬合所有標簽
data = le.transform(data)  # 將原來的標簽轉換為編碼

fit_transform：

le = LabelEncoder()
data = le.fit_transform(data)

inverse_transform：根據編碼反向推出原來類別標簽
```
le.inverse_transform([0,1,2])
# 輸出['A','B','C']
```

繼續AdaBoost。

我們接下來對比一下單一決策樹和集成之間的效果差異。

# 使用單一決策樹建模
from sklearn.tree import DecisionTreeClassifier
tree = DecisionTreeClassifier(criterion='entropy',random_state=1,max_depth=1)
from sklearn.metrics import accuracy_score
tree = tree.fit(X_train,y_train)
y_train_pred = tree.predict(X_train)
y_test_pred = tree.predict(X_test)
tree_train = accuracy_score(y_train,y_train_pred)
tree_test = accuracy_score(y_test,y_test_pred)
print('Decision tree train/test accuracies %.3f/%.3f' % (tree_train,tree_test))

Decision tree train/test accuracies 0.916/0.875

下麵對AdaBoost進行建模：

from sklearn.ensemble import AdaBoostClassifier
ada = AdaBoostClassifier(base_estimator=tree,  # 基分類器
                         n_estimators=500, # 最大迭代次數
                        learning_rate=0.1,
                        random_state= 1)
ada.fit(X_train, y_train)
y_train_pred = ada.predict(X_train)
y_test_pred = ada.predict(X_test)
ada_train = accuracy_score(y_train,y_train_pred)
ada_test = accuracy_score(y_test,y_test_pred)
print('Adaboost train/test accuracies %.3f/%.3f' % (ada_train,ada_test))

Adaboost train/test accuracies 1.000/0.917

可以看見分類精度提升了不少，下麵我們可以觀察他們的決策邊界有什麼不同：

x_min = X_train[:, 0].min() - 1
x_max = X_train[:, 0].max() + 1
y_min = X_train[:, 1].min() - 1
y_max = X_train[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.1),np.arange(y_min, y_max, 0.1))
f, axarr = plt.subplots(nrows=1, ncols=2,sharex='col',sharey='row',figsize=(12, 6))
for idx, clf, tt in zip([0, 1],[tree, ada],['Decision tree', 'Adaboost']):
    clf.fit(X_train, y_train)
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    axarr[idx].contourf(xx, yy, Z, alpha=0.3)
    axarr[idx].scatter(X_train[y_train==0, 0],X_train[y_train==0, 1],c='blue', marker='^')
    axarr[idx].scatter(X_train[y_train==1, 0],X_train[y_train==1, 1],c='red', marker='o')
    axarr[idx].set_title(tt)
axarr[0].set_ylabel('Alcohol', fontsize=12)
plt.tight_layout()
plt.text(0, -0.2,s='OD280/OD315 of diluted wines',ha='center',va='center',fontsize=12,transform=axarr[1].transAxes)
plt.show()

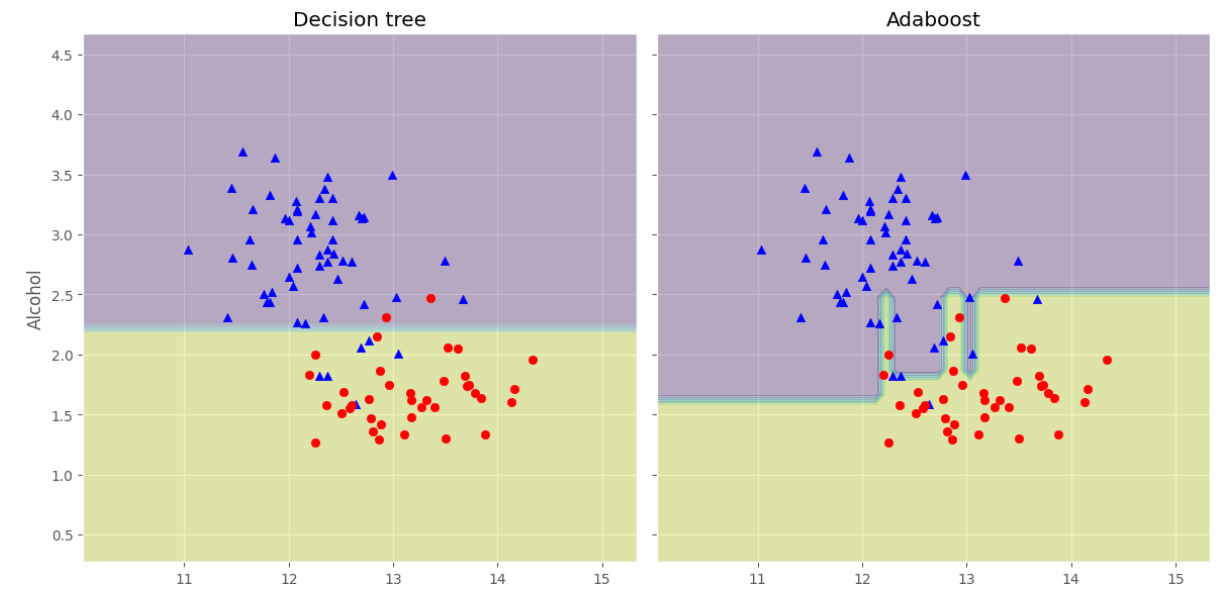
可以看淡AdaBoost的決策邊界比單個決策樹的決策邊界複雜很多。

梯度提升GBDT

這裡的理論解釋用我對西瓜書的學習筆記吧：

GBDT是一種迭代的決策樹演算法，由多個決策樹組成，所有樹的結論累加起來作為最終答案。接下來從這兩個方面進行介紹：Regression Decision Tree(回歸樹)、Gradient Boosting(梯度提升)、Shrinkage

DT

先補充一下決策樹的類別，包含兩種：

分類決策樹：用於預測分類標簽值，例如天氣的類型、用戶的性別等
回歸決策樹：用來預測連續實數值，例如天氣溫度、用戶年齡

這兩者的重要區別在於回歸決策樹的輸出結果可以相加，分類決策樹的輸出結果不可以相加，例如回歸決策樹分別輸出10歲、5歲、2歲，那他們相加得到17歲，可以作為結果使用；但是分類決策樹分別輸出男、男、女，這樣的結果是無法進行相加處理的。因此GBDT中的樹都是回歸樹，GBDT的核心在於累加所有樹的結果作為最終結果。

回歸樹，救贖用樹模型來做回歸問題，其每一片葉子都輸出一個預測值，而這個預測值一般是該片葉子所含訓練集元素輸出的均值，即$c_m=ave(y_i\mid x_i \in leaf_m)$

一般來說常見的回歸決策樹為CART，因此下麵先介紹CART如何應用於回歸問題。

在回歸問題中，CART主要使用均方誤差(mse)或者平均絕對誤差(mae)來作為選擇特征以及選擇劃分點時的依據。因此用於回歸問題時，目標就是要構建出一個函數$f(x)$能夠有效地擬合數據集$D$(樣本數為n)中的元素，使得所選取的度量指標最小，例如取mse，即：
$$
min \frac{1}{n} \sum_{i=0}^{{n}(f(x_i)-y_i)}2
$$
而對於構建好的CART回歸樹來說，假設其存在$M$片葉子，那麼其mse的公式可以寫成：
$$
min \frac{1}{n}\sum_{m=1}^{M}\sum_{x_i \in R_m}(c_m - y_i)^2
$$
其中$R_m$代表第$m$片葉子，而$c_m$代表第$m$片葉子的預測值。

要使得最小化mse，就需要對每一片葉子的mse都進行最小化。由統計學的知識可知道，只需要使**每片葉子的預測值為該片葉子中含有的訓練元素的均值即可，即$c_m=ave(y_i\mid x_i \in leaf_m)$。

因此CART的學習方法就是遍歷每一個變數且遍歷變數中的每一個切分點，尋找能夠使得mse最小的切分變數和切分點，即最小化如下公式：
$$
min_{j,s}[min_{c1}\sum_{x_i\in R_{1{j,s}}}(y_i-c_1)^2+min_{c_2}\sum_{x_i\in R_{2{j,s}}}(y_i-c_2)^2]
$$
另外一個值得瞭解的想法就是為什麼CART必須是二叉樹，其實是因為如果劃分結點增多，即劃分出來的區間也增多，遍歷的難度加大。而如果想要細分為多個區域，實際上只需要讓CART回歸樹的層次更深即可，這樣遍歷難度將小很多。

Gradient Boosting

梯度提升演算法的流程與AdaBoost有點類似，而區別在於AdaBoost的特點在於每一輪是對分類正確和錯誤的樣本分別進行修改權重，而梯度提升演算法的每一輪學習都是為了減少上一輪的誤差，具體可以看以下演算法描述：

Step1、給定訓練數據集T及損失函數L，這裡可以認為損失函數為mse

Step2、初始化：
$$
f_0(x)=argmin_c\sum_{i=1}^{{N}L(y_i,c)=argmin_c\sum_{i=1}}{N}(y_i - f_o(x_i))^2
$$
上式求解出來為：
$$
f_0(x)=\sum_{i=1}^{N} \frac{y_i}{N}=c
$$
Step3、目標基分類器（回歸樹）數目為$M$，對於$m=1,2,...M$：

(1)、對於$i=1,2,...N$，計算
$$
r_{mi}=-[\frac{\partial L(y_i,f(x_i)}{\partial f(x_i)}]{f(x)=f{m-1}(x)}
$$
(2)、對$r_{mi}$進行擬合學習得到一個回歸樹，其葉結點區域為$R_{mj},j=1,2,...J$

(3)、對$j=1,2,...J$，計算該對應葉結點$R_{mj}$的輸出預測值：
$$
c_{mj}=argmin_c\sum_{x_i \in R_{mj}}L(y_i,f_{m-1}(x_i)+c)
$$
(4)、更新$f_m(x)=f_{m-1}(x)+\sum {j=1}^{J}c{mj}I(x \in R_{mj})$

Step4、得到回歸樹：
$$
\hat{f}(x)=f_M(x)=\sum_{m=0}^{M} \sum_{j=1}^{J}c_{mj}I(x\in R_{mj})
$$
為什麼損失函數的負梯度能夠作為回歸問題殘差的近似值呢？：因為對於損失函數為mse來說，其求導的結果其實就是預測值與真實值之間的差值，那麼負梯度也就是我們預測的殘差$(y_i - f(x_i))$，因此只要下一個回歸樹對負梯度進行擬合再對多個回歸樹進行累加，就可以更好地逼近真實值。

Shrinkage

Shrinkage是一種用來對GBDT進行優化，防止其陷入過擬合的方法，其具體思想是：減少每一次迭代對於殘差的收斂程度或者逼近程度，也就是說該思想認為迭代時每一次少逼近一些，然後迭代次數多一些的效果，比每一次多逼近一些，然後迭代次數少一些的效果要更好。那麼具體的實現就是在每個回歸樹的累加前乘上學習率，即：
$$
f_m(x)=f_{m-1}(x)+\gamma\sum_{j=1}^{J}c_{mj}I(x\in R_{mj})
$$

建模實現

下麵對GBDT的模型進行解釋以及建模實現。

引入相關庫：

from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_friedman1
from sklearn.ensemble import GradientBoostingRegressor

GBDT還有一個做分類的模型是GradientBoostingClassifier。

下麵整理一下模型的各個參數：

參數名稱	參數意義
loss	{‘ls’, ‘lad’, ‘huber’, ‘quantile’}, default=’ls’：‘ls’ 指最小二乘回歸. ‘lad’是最小絕對偏差，是僅基於輸入變數的順序信息的高度魯棒的損失函數；‘huber’ 是兩者的結合
quantile	允許分位數回歸（用於alpha指定分位數）
learning_rate	學習率縮小了每棵樹的貢獻learning_rate。在learning_rate和n_estimators之間需要權衡。
n_estimators	要執行的提升次數，可以認為是基分類器的數目
subsample	用於擬合各個基礎學習者的樣本比例。如果小於1.0，則將導致隨機梯度增強
criterion	{'friedman_mse'，'mse'，'mae'}，預設='friedman_mse'：“ mse”是均方誤差，“ mae”是平均絕對誤差。預設值“ friedman_mse”通常是最好的，因為在某些情況下它可以提供更好的近似值。
min_samples_split	拆分內部節點所需的最少樣本數
min_samples_leaf	在葉節點處需要的最小樣本數
min_weight_fraction_leaf	在所有葉節點處（所有輸入樣本）的權重總和中的最小加權分數。如果未提供sample_weight，則樣本的權重相等。
max_depth	各個回歸模型的最大深度。最大深度限制了樹中節點的數量。調整此參數以獲得最佳性能；最佳值取決於輸入變數的相互作用
min_impurity_decrease	如果節點分裂會導致雜質（損失函數）的減少大於或等於該值，則該節點將被分裂
min_impurity_split	提前停止樹木生長的閾值。如果節點的雜質高於閾值，則該節點將分裂
max_features	{‘auto’, ‘sqrt’, ‘log2’}，int或float：尋找最佳分割時要考慮的功能數量

可能各個參數一開始難以理解，但是隨著使用會加深印象的。

X, y = make_friedman1(n_samples=1200, random_state=0, noise=1.0)
X_train, X_test = X[:200], X[200:]
y_train, y_test = y[:200], y[200:]
est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
    max_depth=1, random_state=0, loss='ls').fit(X_train, y_train)
mean_squared_error(y_test, est.predict(X_test))

5.009154859960321

from sklearn.datasets import make_regression
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.model_selection import train_test_split
X, y = make_regression(random_state=0)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, random_state=0)
reg = GradientBoostingRegressor(random_state=0)
reg.fit(X_train, y_train)
reg.score(X_test, y_test)

XGBoost

關於XGBoost的理論，其實它跟GBDT差不多，只不過在泰勒展開時考慮了二階導函數，併在庫實現中增加了很多的優化。而關於其參數的設置也相當複雜，因此這裡簡單介紹其用法即可。

安裝XGBoost

pip install xgboost

數據介面

xgboost庫所使用的數據類型為特殊的DMatrix類型，因此其讀入文件比較特殊：

# 1.LibSVM文本格式文件
dtrain = xgb.DMatrix('train.svm.txt')
dtest = xgb.DMatrix('test.svm.buffer')
# 2.CSV文件(不能含類別文本變數，如果存在文本變數請做特征處理如one-hot)
dtrain = xgb.DMatrix('train.csv?format=csv&label_column=0')
dtest = xgb.DMatrix('test.csv?format=csv&label_column=0')
# 3.NumPy數組
data = np.random.rand(5, 10)  # 5 entities, each contains 10 features
label = np.random.randint(2, size=5)  # binary target
dtrain = xgb.DMatrix(data, label=label)
# 4.scipy.sparse數組
csr = scipy.sparse.csr_matrix((dat, (row, col)))
dtrain = xgb.DMatrix(csr)
# pandas數據框dataframe
data = pandas.DataFrame(np.arange(12).reshape((4,3)), columns=['a', 'b', 'c'])
label = pandas.DataFrame(np.random.randint(2, size=4))
dtrain = xgb.DMatrix(data, label=label)

第一次讀入後可以先保存為對應的二進位文件方便下次讀取：

# 1.保存DMatrix到XGBoost二進位文件中
dtrain = xgb.DMatrix('train.svm.txt')
dtrain.save_binary('train.buffer')
# 2. 缺少的值可以用DMatrix構造函數中的預設值替換：
dtrain = xgb.DMatrix(data, label=label, missing=-999.0)
# 3.可以在需要時設置權重：
w = np.random.rand(5, 1)
dtrain = xgb.DMatrix(data, label=label, missing=-999.0, weight=w)

參數設置

import pandas as pd
df_wine = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/wine/wine.data',header=None)
df_wine.columns = ['Class label', 'Alcohol','Malic acid', 'Ash','Alcalinity of ash','Magnesium', 'Total phenols',
                   'Flavanoids', 'Nonflavanoid phenols','Proanthocyanins','Color intensity', 'Hue','OD280/OD315 of diluted wines','Proline'] 
df_wine = df_wine[df_wine['Class label'] != 1]  # drop 1 class      
y = df_wine['Class label'].values
X = df_wine[['Alcohol','OD280/OD315 of diluted wines']].values
from sklearn.model_selection import train_test_split  # 切分訓練集與測試集
from sklearn.preprocessing import LabelEncoder   # 標簽化分類變數
import xgboost as xgb
le = LabelEncoder()
y = le.fit_transform(y)
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.2,
                                                 random_state=1,stratify=y)
# 構造成目標類型的數據
dtrain = xgb.DMatrix(X_train, label = y_train)
dtest = xgb.DMatrix(X_test)

# booster參數
params = {
    "booster": 'gbtree',  # 基分類器
    "objective":  "multi:softmax",  # 使用softmax
    "num_class": 10,  # 類別數
    "gamma":0.1,  # 用於控制損失函數大於gamma時就剪枝
    "max_depth": 12,  # 構造樹的深度，越大越容易過擬合
    "lambda":  2,  # 用來控制正則化參數
    "subsample": 0.7,  # 隨機採樣70%作為訓練樣本
    "colsample_bytree": 0.7,  # 生成樹時進行列採樣，相當於隨機子空間
    "min_child_weight":3,
    'verbosity':0,  # 設置成1則沒有運行信息輸出，設置成0則有,原文中這裡的silent已經在新版本中不使用了
    "eta": 0.007,  # 相當於學習率
    "seed": 1000,  # 隨機數種子
    "nthread":4,   # 線程數
    "eval_metric": "auc"
}
plst = list(params.items())  # 這裡必須加上list才能夠使用後續的copy

這裡如果發現報錯為：

Parameters: { "silent" } are not used.

那是因為參數設置中新版本已經取消了silent參數，將其更改為verbosity即可。

如果在後續中發現：

'dict_items' object has no attribute 'copy'

那是因為我們沒有將items的返回變成list，像我上面那麼改即可。

訓練及預測

num_round = 10
bst = xgb.train(plst, dtrain ,num_round)
# 可以加上early_stoppint_rounds = 10來設置早停機制
# 如果要指定驗證集，就是
# evallist = [(deval,'eval'),(dtrain, 'train')]
# bst = xgb.train(plst, dtrain, num_round, evallist)

ypred = bst.predict(dtest)  # 進行預測，跟sklearn的模型一致
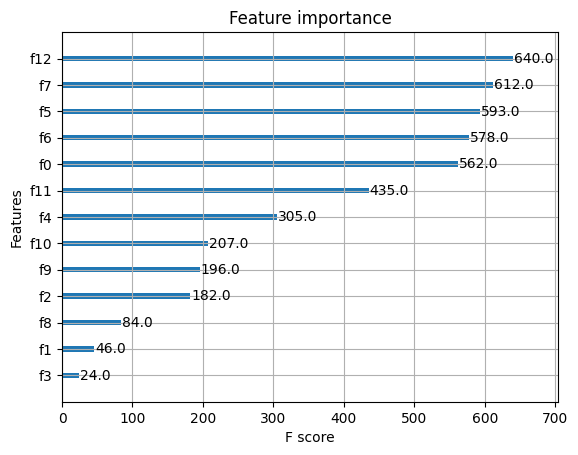
xgb.plot_importance(bst)  # 繪製特征重要性的圖

<AxesSubplot:title={'center':'Feature importance'}, xlabel='F score', ylabel='Features'>

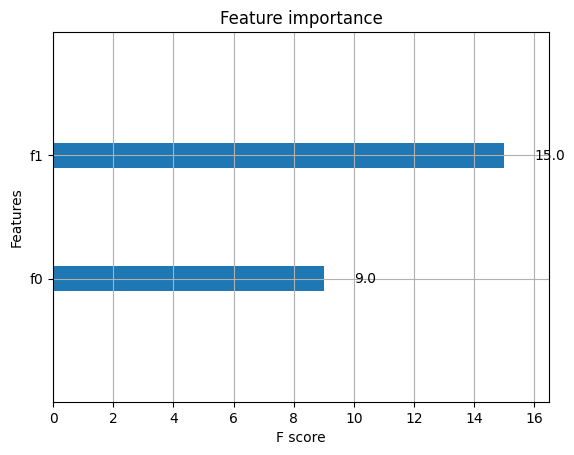
特征重要性

模型保存與載入

bst.save_model("model_new_1121.model")
bst.dump_model("dump.raw.txt")
bst_new = xgb.Booster({'nthread':4})  # 先初始化參數
bst_new.load_model("model_new_1121.model")

簡單算例

分類案例

from sklearn.datasets import load_iris
import xgboost as xgb
from xgboost import plot_importance
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score   # 準確率
# 載入樣本數據集
iris = load_iris()
X,y = iris.data,iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, 
                                                    random_state=1234565) # 數據集分割
# 演算法參數
params = {
    'booster': 'gbtree',
    'objective': 'multi:softmax',
    'num_class': 3,
    'gamma': 0.1,
    'max_depth': 6,
    'lambda': 2,
    'subsample': 0.7,
    'colsample_bytree': 0.75,
    'min_child_weight': 3,
    'verbosity': 0,
    'eta': 0.1,
    'seed': 1,
    'nthread': 4,
}
plst = list(params.items())
dtrain = xgb.DMatrix(X_train, y_train) # 生成數據集格式
num_rounds = 500
model = xgb.train(plst, dtrain, num_rounds) # xgboost模型訓練
# 對測試集進行預測
dtest = xgb.DMatrix(X_test)
y_pred = model.predict(dtest)

# 計算準確率
accuracy = accuracy_score(y_test,y_pred)
print("accuarcy: %.2f%%" % (accuracy*100.0))

# 顯示重要特征
plot_importance(model)
plt.show()

accuarcy: 96.67%

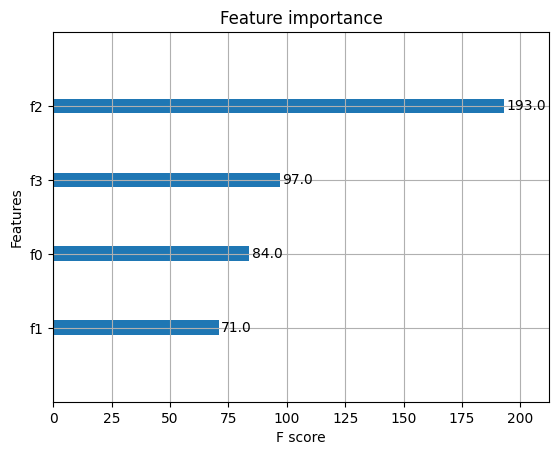
特征重要性2

回歸案例

import xgboost as xgb
from xgboost import plot_importance
from matplotlib import pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_boston
from sklearn.metrics import mean_squared_error

# 載入數據集
boston = load_boston()
X,y = boston.data,boston.target

# XGBoost訓練過程
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

params = {
    'booster': 'gbtree',
    'objective': 'reg:squarederror',  # 設置為回歸，採用平方誤差
    'gamma': 0.1,
    'max_depth': 5,
    'lambda': 3,
    'subsample': 0.7,
    'colsample_bytree': 0.7,
    'min_child_weight': 3,
    'verbosity': 1,
    'eta': 0.1,
    'seed': 1000,
    'nthread': 4,
}
dtrain = xgb.DMatrix(X_train, y_train)
num_rounds = 300
plst = list(params.items())
model = xgb.train(plst, dtrain, num_rounds)
# 對測試集進行預測
dtest = xgb.DMatrix(X_test)
ans = model.predict(dtest)

# 顯示重要特征
plot_importance(model)
plt.show()

特征重要性3

XGBoost的調參

該模型的調參一般步驟為：

確定學習速率和提升參數調優的初始值
max_depth 和 min_child_weight 參數調優
gamma參數調優
subsample 和 colsample_bytree 參數優
正則化參數alpha調優
降低學習速率和使用更多的決策樹

可以使用網格搜索來進行調優：

import xgboost as xgb
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import roc_auc_score

iris = load_iris()
X,y = iris.data,iris.target
col = iris.target_names 
train_x, valid_x, train_y, valid_y = train_test_split(X, y, test_size=0.3, random_state=1)   # 分訓練集和驗證集
parameters = {
              'max_depth': [5, 10, 15, 20, 25],
              'learning_rate': [0.01, 0.02, 0.05, 0.1, 0.15],
              'n_estimators': [500, 1000, 2000, 3000, 5000],
              'min_child_weight': [0, 2, 5, 10, 20],
              'max_delta_step': [0, 0.2, 0.6, 1, 2],
              'subsample': [0.6, 0.7, 0.8, 0.85, 0.95],
              'colsample_bytree': [0.5, 0.6, 0.7, 0.8, 0.9],
              'reg_alpha': [0, 0.25, 0.5, 0.75, 1],
              'reg_lambda': [0.2, 0.4, 0.6, 0.8, 1],
              'scale_pos_weight': [0.2, 0.4, 0.6, 0.8, 1]

}

xlf = xgb.XGBClassifier(max_depth=10,
            learning_rate=0.01,
            n_estimators=2000,
            silent=True,
            objective='multi:softmax',
            num_class=3 ,          
            nthread=-1,
            gamma=0,
            min_child_weight=1,
            max_delta_step=0,
            subsample=0.85,
            colsample_bytree=0.7,
            colsample_bylevel=1,
            reg_alpha=0,
            reg_lambda=1,
            scale_pos_weight=1,
            seed=0,
            missing=None)
# 需要先給模型一定的初始值
gs = GridSearchCV(xlf, param_grid=parameters, scoring='accuracy', cv=3)
gs.fit(train_x, train_y)

print("Best score: %0.3f" % gs.best_score_)
print("Best parameters set: %s" % gs.best_params_ )

Best score: 0.933
Best parameters set: {'max_depth': 5}

LightGBM演算法

LightGBM也是像XGBoost一樣，是一類集成演算法，他跟XGBoost總體來說是一樣的，演算法本質上與Xgboost沒有出入，只是在XGBoost的基礎上進行了優化。

其調優過程也是一個很複雜的學問。這裡就附上課程調優代碼吧：

import lightgbm as lgb
from sklearn import metrics
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
 
canceData=load_breast_cancer()
X=canceData.data
y=canceData.target
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=0,test_size=0.2)
 
### 數據轉換
print('數據轉換')
lgb_train = lgb.Dataset(X_train, y_train, free_raw_data=False)
lgb_eval = lgb.Dataset(X_test, y_test, reference=lgb_train,free_raw_data=False)
 
### 設置初始參數--不含交叉驗證參數
print('設置參數')
params = {
          'boosting_type': 'gbdt',
          'objective': 'binary',
          'metric': 'auc',
          'nthread':4,
          'learning_rate':0.1
          }
 
### 交叉驗證(調參)
print('交叉驗證')
max_auc = float('0')
best_params = {}
 
# 準確率
print("調參1：提高準確率")
for num_leaves in range(5,100,5):
    for max_depth in range(3,8,1):
        params['num_leaves'] = num_leaves
        params['max_depth'] = max_depth
 
        cv_results = lgb.cv(
                            params,
                            lgb_train,
                            seed=1,
                            nfold=5,
                            metrics=['auc'],
                            early_stopping_rounds=10,
                            verbose_eval=True
                            )
            
        mean_auc = pd.Series(cv_results['auc-mean']).max()
        boost_rounds = pd.Series(cv_results['auc-mean']).idxmax()
            
        if mean_auc >= max_auc:
            max_auc = mean_auc
            best_params['num_leaves'] = num_leaves
            best_params['max_depth'] = max_depth
if 'num_leaves' and 'max_depth' in best_params.keys():          
    params['num_leaves'] = best_params['num_leaves']
    params['max_depth'] = best_params['max_depth']
 
# 過擬合
print("調參2：降低過擬合")
for max_bin in range(5,256,10):
    for min_data_in_leaf in range(1,102,10):
            params['max_bin'] = max_bin
            params['min_data_in_leaf'] = min_data_in_leaf
            
            cv_results = lgb.cv(
                                params,
                                lgb_train,
                                seed=1,
                                nfold=5,
                                metrics=['auc'],
                                early_stopping_rounds=10,
                                verbose_eval=True
                                )
                    
            mean_auc = pd.Series(cv_results['auc-mean']).max()
            boost_rounds = pd.Series(cv_results['auc-mean']).idxmax()
 
            if mean_auc >= max_auc:
                max_auc = mean_auc
                best_params['max_bin']= max_bin
                best_params['min_data_in_leaf'] = min_data_in_leaf
if 'max_bin' and 'min_data_in_leaf' in best_params.keys():
    params['min_data_in_leaf'] = best_params['min_data_in_leaf']
    params['max_bin'] = best_params['max_bin']
 
print("調參3：降低過擬合")
for feature_fraction in [0.6,0.7,0.8,0.9,1.0]:
    for bagging_fraction in [0.6,0.7,0.8,0.9,1.0]:
        for bagging_freq in range(0,50,5):
            params['feature_fraction'] = feature_fraction
            params['bagging_fraction'] = bagging_fraction
            params['bagging_freq'] = bagging_freq
            
            cv_results = lgb.cv(
                                params,
                                lgb_train,
                                seed=1,
                                nfold=5,
                                metrics=['auc'],
                                early_stopping_rounds=10,
                                verbose_eval=True
                                )
                    
            mean_auc = pd.Series(cv_results['auc-mean']).max()
            boost_rounds = pd.Series(cv_results['auc-mean']).idxmax()
 
            if mean_auc >= max_auc:
                max_auc=mean_auc
                best_params['feature_fraction'] = feature_fraction
                best_params['bagging_fraction'] = bagging_fraction
                best_params['bagging_freq'] = bagging_freq
 
if 'feature_fraction' and 'bagging_fraction' and 'bagging_freq' in best_params.keys():
    params['feature_fraction'] = best_params['feature_fraction']
    params['bagging_fraction'] = best_params['bagging_fraction']
    params['bagging_freq'] = best_params['bagging_freq']
 
 
print("調參4：降低過擬合")
for lambda_l1 in [1e-5,1e-3,1e-1,0.0,0.1,0.3,0.5,0.7,0.9,1.0]:
    for lambda_l2 in [1e-5,1e-3,1e-1,0.0,0.1,0.4,0.6,0.7,0.9,1.0]:
        params['lambda_l1'] = lambda_l1
        params['lambda_l2'] = lambda_l2
        cv_results = lgb.cv(
                            params,
                            lgb_train,
                            seed=1,
                            nfold=5,
                            metrics=['auc'],
                            early_stopping_rounds=10,
                            verbose_eval=True
                            )
                
        mean_auc = pd.Series(cv_results['auc-mean']).max()
        boost_rounds = pd.Series(cv_results['auc-mean']).idxmax()
 
        if mean_auc >= max_auc:
            max_auc=mean_auc
            best_params['lambda_l1'] = lambda_l1
            best_params['lambda_l2'] = lambda_l2
if 'lambda_l1' and 'lambda_l2' in best_params.keys():
    params['lambda_l1'] = best_params['lambda_l1']
    params['lambda_l2'] = best_params['lambda_l2']
 
print("調參5：降低過擬合2")
for min_split_gain in [0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0]:
    params['min_split_gain'] = min_split_gain
    
    cv_results = lgb.cv(
                        params,
                        lgb_train,
                        seed=1,
                        nfold=5,
                        metrics=['auc'],
                        early_stopping_rounds=10,
                        verbose_eval=True
                        )
            
    mean_auc = pd.Series(cv_results['auc-mean']).max()
    boost_rounds = pd.Series(cv_results['auc-mean']).idxmax()
 
    if mean_auc >= max_auc:
        max_auc=mean_auc
        
        best_params['min_split_gain'] = min_split_gain
if 'min_split_gain' in best_params.keys():
    params['min_split_gain'] = best_params['min_split_gain']
 
print(best_params)

{'bagging_fraction': 0.7,
'bagging_freq': 30,
'feature_fraction': 0.8,
'lambda_l1': 0.1,
'lambda_l2': 0.0,
'max_bin': 255,
'max_depth': 4,
'min_data_in_leaf': 81,
'min_split_gain': 0.1,
'num_leaves': 10}

Blending與Stacking

Stacking，這個集成方法在比賽中被稱為“懶人”演算法，因為它不需要花費過多時間的調參就可以得到一個效果不錯的演算法。

Stacking集成演算法可以理解為一個兩層的集成，第一層含有多個基礎分類器，把預測的結果(元特征)提供給第二層，而第二層的分類器通常是邏輯回歸，他把一層分類器的結果當做特征做擬合輸出預測結果。

而Blending就是簡化版的Stacking，因此我們先對前者進行介紹。

Blending集成學習演算法

演算法流程

Blending的演算法流程為：

將數據集劃分為訓練集與測試集，訓練集再劃分為訓練集與驗證集
創建第一層的多個模型（可同質也可異質），然後對訓練集進行學習
第一層的模型訓練完成後對驗證集和測試集做出預測，假設K個模型，那麼就得到$A_1,...,A_K$和$B_1,...,B_K$，其中每個代表一個基分類器對驗證集或測試集的所有結果輸出。
創建第二層的分類器，其將$A_1,...,A_K$作為訓練數據集，那麼樣本數目就是驗證集的樣本數目，特征數目就是K，將真實的驗證集標簽作為標簽，從而來訓練該分類器
對測試集的預測則是將$B_1,...,B_K$作為特征，用第二層的分類器進行預測。

具體實現

具體的實現如下：

import numpy as np
import pandas as pd 
import matplotlib.pyplot as plt
plt.style.use("ggplot")
%matplotlib inline
import seaborn as sns
# 創建數據
from sklearn import datasets 
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
data, target = make_blobs(n_samples=10000, centers=2, random_state=1, cluster_std=1.0 )
## 創建訓練集和測試集
X_train1,X_test,y_train1,y_test = train_test_split(data, target, test_size=0.2, random_state=1)
## 創建訓練集和驗證集
X_train,X_val,y_train,y_val = train_test_split(X_train1, y_train1, test_size=0.3, random_state=1)
print("The shape of training X:",X_train.shape)
print("The shape of training y:",y_train.shape)
print("The shape of test X:",X_test.shape)
print("The shape of test y:",y_test.shape)
print("The shape of validation X:",X_val.shape)
print("The shape of validation y:",y_val.shape)

The shape of training X: (5600, 2)
The shape of training y: (5600,)
The shape of test X: (2000, 2)
The shape of test y: (2000,)
The shape of validation X: (2400, 2)
The shape of validation y: (2400,)

#  設置第一層分類器
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier

clfs = [SVC(probability = True),RandomForestClassifier(n_estimators=5, n_jobs=-1, criterion='gini'),KNeighborsClassifier()]

# 設置第二層分類器
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
# 輸出第一層的驗證集結果與測試集結果
val_features = np.zeros((X_val.shape[0],len(clfs)))  # 初始化驗證集結果
test_features = np.zeros((X_test.shape[0],len(clfs)))  # 初始化測試集結果

for i,clf in enumerate(clfs):
    clf.fit(X_train,y_train)
    # porba函數得到的是對於每個類別的預測分數，取出第一列代表每個樣本為第一類的概率
    val_feature = clf.predict_proba(X_val)[:, 1]
    test_feature = clf.predict_proba(X_test)[:,1]
    val_features[:,i] = val_feature
    test_features[:,i] = test_feature
# 將第一層的驗證集的結果輸入第二層訓練第二層分類器
lr.fit(val_features,y_val)
# 輸出預測的結果
from sklearn.model_selection import cross_val_score
cross_val_score(lr,test_features,y_test,cv=5)

array([1., 1., 1., 1., 1.])

可以看到交叉驗證的結果很好。

對於小作業我總有些疑問，那就是這個iris數據的特征為4，然後預測類別數為3，那麼首先是特征為4超過3維度，應該怎麼決策邊界，難道捨棄一些維度嗎？其次是類別數為3，那麼在計算的時候取的是[;1]也就是類別為1的概率，那麼只取這個作為下一層的特征是否足夠，因為類別為0和類別為2的概率完全捨棄的話不行吧。

Stacking

演算法流程

下麵這張圖可以很好的理解流程：

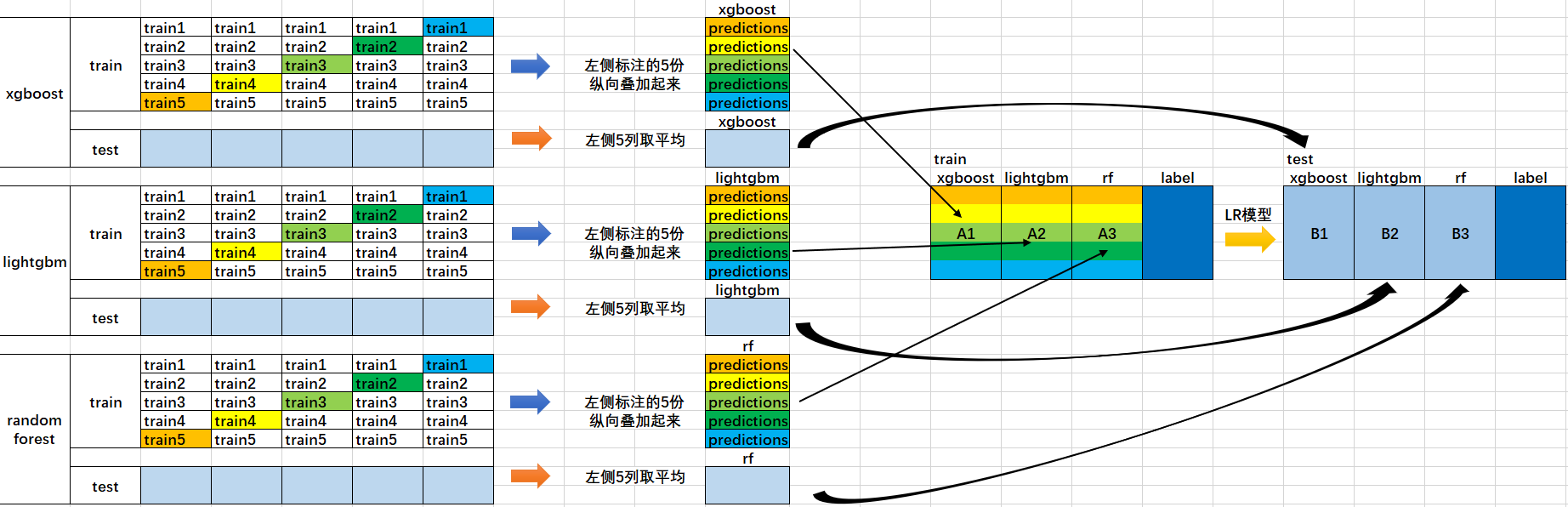
首先將所有數據劃分測試集和訓練集，假設訓練集總共有10000行，測試集總共2500行，對第一層的分類器進行5折交叉驗證，那麼驗證集就劃分為2000行，訓練集為8000行。
每次驗證就相當於使用8000條訓練數據去訓練模型然後用2000條驗證數據去驗證，並且每一次都將訓練出來的模型對測試集的2500條數據進行預測，那麼經過5次交叉驗證，對於每個基分類器可以得到中間的$5\times 2000$的五份驗證集數據，以及$5\times 2500$的五份測試集的預測結果
接下來將驗證集拼成10000行長的矩陣，記為$A_1$（對於第1個基分類器），而對於$5\times 2500$行的測試集的預測結果進行加權平均，得到2500行1列的矩陣，記為$B_1$
那麼假設這裡是3個基分類器，因此有$A_1,A_2,A_3,B_1,B_2,B_3$六個矩陣，接下來將$A_1,A_2,A_3$矩陣拼成10000行3列的矩陣作為訓練數據集，而驗證集的真實標簽作為訓練數據的標簽；將$B_1,B_2,B_3$拼成2500行3列的矩陣作為測試數據集合。
那麼對下層的學習器進行訓練

具體代碼

from sklearn import datasets
iris = datasets.load_iris()
X, y = iris.data[:, 1:3], iris.target  # 只取出兩個特征
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB 
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifier

RANDOM_SEED = 42

clf1 = KNeighborsClassifier(n_neighbors = 1)
clf2 = RandomForestClassifier(random_state = RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()

sclf = StackingCVClassifier(classifiers = [clf1, clf2, clf3],  # 第一層的分類器
                           meta_classifier = lr,  # 第二層的分類器
                           random_state = RANDOM_SEED)
print("3折交叉驗證：\n")
for clf, label in zip([clf1, clf2, clf3, sclf], ['KNN','RandomForest','Naive Bayes',
                                                'Stack']):
    scores = cross_val_score(clf, X, y, cv = 3, scoring = 'accuracy')
    print("Accuracy: %0.2f (+/- %0.2f) [%s]" % (scores.mean(), scores.std(), label))

3折交叉驗證：

Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.95 (+/- 0.01) [RandomForest]
Accuracy: 0.91 (+/- 0.02) [Naive Bayes]
Accuracy: 0.93 (+/- 0.02) [Stack]

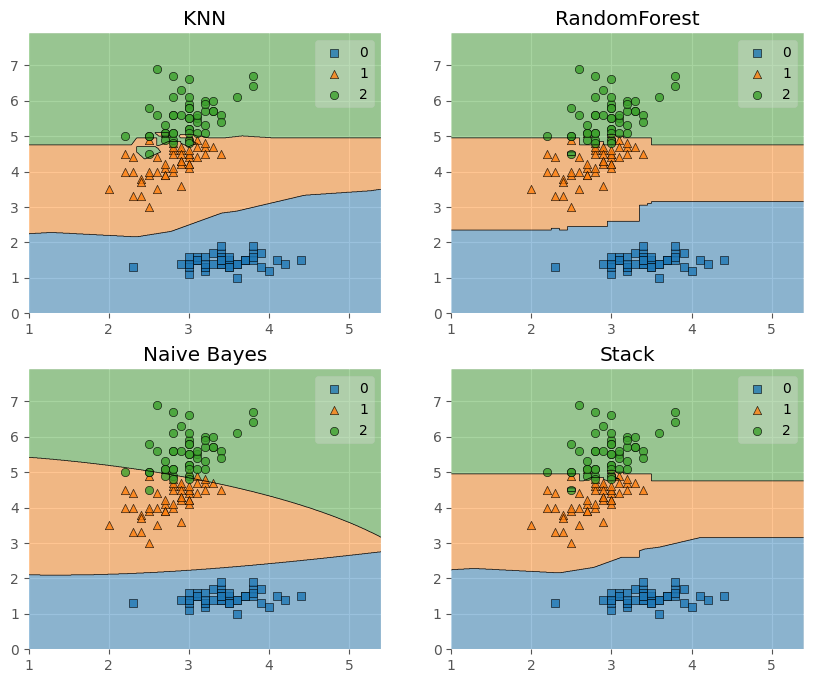
接下來嘗試將決策邊界畫出：

from mlxtend.plotting import plot_decision_regions
import matplotlib.gridspec as gridspec
import itertools


gs = gridspec.GridSpec(2,2)
# 可以理解為將子圖劃分為了2*2的區域
fig = plt.figure(figsize = (10,8))

for clf, lab, grd in zip([clf1, clf2, clf3, sclf], ['KNN',
                                                    'RandomForest',
                                                    'Naive Bayes',
                                                    'Stack'],
                        itertools.product([0,1],repeat=2)):
    clf.fit(X, y)
    ax = plt.subplot(gs[grd[0],grd[1]])
    # grd依次為(0,0),(0,1),(1,0),(1,1)，那麼傳入到gs中就可以得到指定的區域
    fig = plot_decision_regions(X = X, y = y, clf = clf)
    plt.title(lab)
    
plt.show()

這裡補充兩個第一次見到的函數：

itertools.product([0,1],repeat = 2)：該模塊下的product函數一般是傳進入兩個集合，例如傳進入[0,1],[1,2]然後返回[(0,1),(0,2),(1,1),(1,2)]，那麼這裡只傳進去一個參數然後repeat=2相當於傳進去[0,1],[0,1]，產生[(0,0),(0,1),(1,0),(1,1)]，如果repeat=3就是
```
(0, 0, 0)
(0, 0, 1)
(0, 1, 0)
(0, 1, 1)
(1, 0, 0)
(1, 0, 1)
(1, 1, 0)
(1, 1, 1)
```
gs = gridspec.GridSpec(2,2)：這個函數相當於我將子圖劃分為2*2總共4個區域，那麼在下麵subplot中就可以例如調用gs[0,1]來獲取(0,1)這個區域，下麵的例子或者更好理解：
```
plt.figure()

gs=gridspec.GridSpec(3,3)#分為3行3列
ax1=plt.subplot(gs[0,:])
ax1=plt.subplot(gs[1,:2])
ax1=plt.subplot(gs[1:,2])
ax1=plt.subplot(gs[-1,0])
ax1=plt.subplot(gs[-1,-2])
```

繼續回到Stacking中。

前面我們是使用第一層的分類器其輸出作為第二層的輸入，那麼如果希望使用第一層所有基分類器所產生的的類別概率值作為第二層分類器的數目，需要在StackingClassifier 中增加一個參數設置：use_probas = True。還有一個參數設置average_probas = True,那麼這些基分類器所產出的概率值將按照列被平均，否則會拼接

我們來進行嘗試：

clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=1)
clf3 = GaussianNB()
lr = LogisticRegression()

sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
                            use_probas=True,  #  使用概率
                            meta_classifier=lr,
                            random_state=42)

print('3折交叉驗證：')

for clf, label in zip([clf1, clf2, clf3, sclf], 
                      ['KNN', 
                       'Random Forest', 
                       'Naive Bayes',
                       'StackingClassifier']):

    scores = cross_val_score(clf, X, y, cv=3, scoring='accuracy')
    print("Accuracy: %0.2f (+/- %0.2f) [%s]" 
          % (scores.mean(), scores.std(), label))

3折交叉驗證：
Accuracy: 0.91 (+/- 0.01) [KNN]
Accuracy: 0.95 (+/- 0.01) [Random Forest]
Accuracy: 0.91 (+/- 0.02) [Naive Bayes]
Accuracy: 0.95 (+/- 0.02) [StackingClassifier]

另外，還可以跟網格搜索相結合：

from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB 
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from mlxtend.classifier import StackingCVClassifier


clf1 = KNeighborsClassifier(n_neighbors=1)
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = GaussianNB()
lr = LogisticRegression()

sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3], 
                            meta_classifier=lr,
                            random_state=42)

params = {'kneighborsclassifier__n_neighbors': [1, 5],
          'randomforestclassifier__n_estimators': [10, 50],
          'meta_classifier__C': [0.1, 10.0]}# 
grid = GridSearchCV(estimator=sclf,  # 分類為stacking 
                    param_grid=params, # 設置的參數
                    cv=5,
                    refit=True)  
#最後一個參數代表在搜索參數結束後，用最佳參數結果再次fit一遍全部數據集

grid.fit(X, y)

cv_keys = ('mean_test_score', 'std_test_score', 'params')

for r,_ in enumerate(grid.cv_results_['mean_test_score']):
    print("%0.3f +/- %0.2f %r"
          % (grid.cv_results_[cv_keys[0]][r],
             grid.cv_results_[cv_keys[1]][r] / 2.0,
             grid.cv_results_[cv_keys[2]][r]))
print('Best parameters: %s' % grid.best_params_)
print('Accuracy: %.2f' % grid.best_score_)

0.947 +/- 0.03 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.933 +/- 0.02 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.940 +/- 0.02 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.940 +/- 0.02 {'kneighborsclassifier__n_neighbors': 1, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 50}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 10}
0.953 +/- 0.02 {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 10.0, 'randomforestclassifier__n_estimators': 50}
Best parameters: {'kneighborsclassifier__n_neighbors': 5, 'meta_classifier__C': 0.1, 'randomforestclassifier__n_estimators': 10}
Accuracy: 0.95

而如果希望在演算法中多次使用某個模型，就可以在參數網格中添加一個附加的數字尾碼：

params = {'kneighborsclassifier-1__n_neighbors': [1, 5],
          'kneighborsclassifier-2__n_neighbors': [1, 5],
          'randomforestclassifier__n_estimators': [10, 50],
          'meta_classifier__C': [0.1, 10.0]}

我們還可以結合隨機子空間的思想，為Stacking第一層的不同子模型設置不同的特征：

from sklearn.datasets import load_iris
from mlxtend.classifier import StackingCVClassifier
from mlxtend.feature_selection import ColumnSelector
from sklearn.pipeline import make_pipeline
from sklearn.linear_model import LogisticRegression

iris = load_iris()
X = iris.data
y = iris.target

pipe1 = make_pipeline(ColumnSelector(cols=(0, 2)),  # 選擇第0,2列
                      LogisticRegression())  # 可以理解為先挑選特征再以基分類器為邏輯回歸
pipe2 = make_pipeline(ColumnSelector(cols=(1, 2, 3)),  # 選擇第1,2,3列
                      LogisticRegression())  # 兩個基分類器都是邏輯回歸
sclf = StackingCVClassifier(classifiers=[pipe1, pipe2], 
                            # 兩個基分類器區別在於使用特征不同
                            meta_classifier=LogisticRegression(),
                            random_state=42)

sclf.fit(X, y)

下麵我們可以畫ROC曲線：

from sklearn import model_selection
from sklearn.linear_model import LogisticRegression
from sklearn.neighbors import KNeighborsClassifier
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier
from mlxtend.classifier import StackingCVClassifier
from sklearn.metrics import roc_curve, auc
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.preprocessing import label_binarize
from sklearn.multiclass import OneVsRestClassifier

iris = datasets.load_iris()
X, y = iris.data[:, [0, 1]], iris.target  # 只用了前兩個特征

y = label_binarize(y, classes = [0,1,2])
# 因為y裡面有三個類別，分類標註為0,1,2，這裡是將y變換為一個n*3的矩陣
# 每一行為3代表類別數目為3，然後如果y是第0類就是100，第一類就是010，第二類就是001
# 關鍵在於後面的classes如何制定，如果是[0,2,1]那麼是第二類就是010，第一類是001
n_classes = y.shape[1]

RANDOM_SEED = 42

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33, 
                                                    random_state=RANDOM_SEED)

clf1 =  LogisticRegression()
clf2 = RandomForestClassifier(random_state=RANDOM_SEED)
clf3 = SVC(random_state=RANDOM_SEED)
lr = LogisticRegression()

sclf = StackingCVClassifier(classifiers=[clf1, clf2, clf3],
                            meta_classifier=lr)

classifier = OneVsRestClassifier(sclf)  
# 這個對象在擬合時會對每一類學習一個分類器，用來做二分類，分別該類和其他所有類
y_score = classifier.fit(X_train, y_train).decision_function(X_test)
# decision_function是預測X_test在決策邊界的哪一邊，然後距離有多大，可以認為是評估指標
# Compute ROC curve and ROC area for each class
fpr = dict()
tpr = dict()
roc_auc = dict()
for i in range(n_classes):
    fpr[i], tpr[i], _ = roc_curve(y_test[:, i], y_score[:, i])
    roc_auc[i] = auc(fpr[i], tpr[i])

# Compute micro-average ROC curve and ROC area
fpr["micro"], tpr["micro"], _ = roc_curve(y_test.ravel(), y_score.ravel())
roc_auc["micro"] = auc(fpr["micro"], tpr["micro"])

plt.figure()
lw = 2
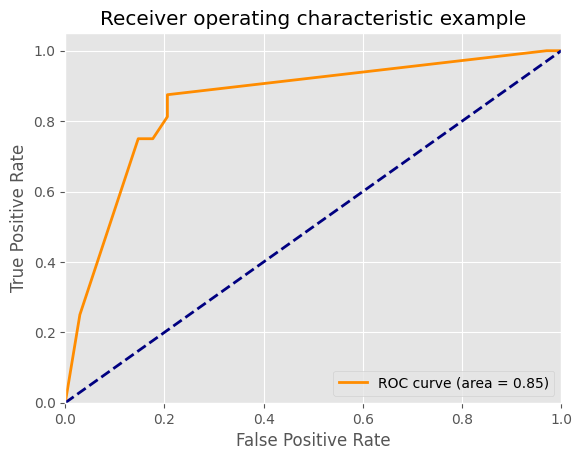
plt.plot(fpr[2], tpr[2], color='darkorange',
         lw=lw, label='ROC curve (area = %0.2f)' % roc_auc[2])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()

下載 ()

集成學習案例1——幸福感預測

背景介紹

此案例是一個數據挖掘類型的比賽——幸福感預測的baseline。比賽的數據使用的是官方的《中國綜合社會調查（CGSS）》文件中的調查結果中的數據，其共包含有139個維度的特征，包括個體變數（性別、年齡、地域、職業、健康、婚姻與政治面貌等等）、家庭變數（父母、配偶、子女、家庭資本等等）、社會態度（公平、信用、公共服務）等特征。賽題要求使用以上 139 維的特征，使用 8000 餘組數據進行對於個人幸福感的預測（預測值為1，2，3，4，5，其中1代表幸福感最低，5代表幸福感最高）

具體代碼

導入需要的包

import os
import time 
import pandas as pd
import numpy as np
import seaborn as sns
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC, LinearSVC
from sklearn.ensemble import RandomForestClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.naive_bayes import GaussianNB
from sklearn.linear_model import Perceptron
from sklearn.linear_model import SGDClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn import metrics
from datetime import datetime
import matplotlib.pyplot as plt
from sklearn.metrics import roc_auc_score, roc_curve, mean_squared_error,mean_absolute_error, f1_score
import lightgbm as lgb
import xgboost as xgb
from sklearn.ensemble import RandomForestRegressor as rfr
from sklearn.ensemble import ExtraTreesRegressor as etr
from sklearn.linear_model import BayesianRidge as br
from sklearn.ensemble import GradientBoostingRegressor as gbr
from sklearn.linear_model import Ridge
from sklearn.linear_model import Lasso
from sklearn.linear_model import LinearRegression as lr
from sklearn.linear_model import ElasticNet as en
from sklearn.kernel_ridge import KernelRidge as kr
from sklearn.model_selection import  KFold, StratifiedKFold,GroupKFold, RepeatedKFold
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn import preprocessing
import logging
import warnings

warnings.filterwarnings('ignore') #消除warning

導入數據集

train = pd.read_csv("train.csv", parse_dates=['survey_time'],encoding='latin-1')
# 第二個參數代表把那一列轉換為時間類型
test = pd.read_csv("test.csv", parse_dates=['survey_time'],encoding='latin-1') 
#latin-1向下相容ASCII

train = train[train["happiness"] != -8].reset_index(drop=True)
# =8代表沒有回答是否幸福因此不要這些，reset_index是重置索引，因為行數變化了

train_data_copy = train.copy()  # 完全刪除掉-8的行
target_col = "happiness"
target = train_data_copy[target_col]
del train_data_copy[target_col]

data = pd.concat([train_data_copy, test], axis = 0, ignore_index = True)
# 把他們按照行疊在一起

數據預處理

數據中出現的主要負數值是-1,-2，-3，-8，因此分別定義函數可以處理。

#make feature +5
#csv中有複數值：-1、-2、-3、-8，將他們視為有問題的特征，但是不刪去
def getres1(row):
    return len([x for x in row.values if type(x)==int and x<0])

def getres2(row):
    return len([x for x in row.values if type(x)==int and x==-8])

def getres3(row):
    return len([x for x in row.values if type(x)==int and x==-1])

def getres4(row):
    return len([x for x in row.values if type(x)==int and x==-2])

def getres5(row):
    return len([x for x in row.values if type(x)==int and x==-3])

#檢查數據
# 這裡的意思就是將函數應用到表格中，而axis=1是應用到每一行，因此得到新的特征行數跟原來
# 是一樣的，統計了該行為負數的個數
data['neg1'] = data[data.columns].apply(lambda row:getres1(row),axis=1)
data.loc[data['neg1']>20,'neg1'] = 20  #平滑處理
data['neg2'] = data[data.columns].apply(lambda row:getres2(row),axis=1)
data['neg3'] = data[data.columns].apply(lambda row:getres3(row),axis=1)
data['neg4'] = data[data.columns].apply(lambda row:getres4(row),axis=1)
data['neg5'] = data[data.columns].apply(lambda row:getres5(row),axis=1)

而對於缺失值的填補，需要針對特征加上自己的理解，例如如果家庭成員缺失值，那麼就填補為1，例如家庭收入確實，那麼可以填補為整個特征的平均值等等，這部分可以自己發揮想象力，採用fillna進行填補。

先查看哪些列存在缺失值需要填補：

data.isnull().sum()[data.isnull().sum() > 0]

edu_other          10950
edu_status          1569
edu_yr              2754
join_party          9831
property_other     10867
hukou_loc              4
social_neighbor     1096
social_friend       1096
work_status         6932
work_yr             6932
work_type           6931
work_manage         6931
family_income          1
invest_other       10911
minor_child         1447
marital_1st         1128
s_birth             2365
marital_now         2445
s_edu               2365
s_political         2365
s_hukou             2365
s_income            2365
s_work_exper        2365
s_work_status       7437
s_work_type         7437
dtype: int64

那麼對以上這些特征進行處理：

data['work_status'] = data['work_status'].fillna(0)
data['work_yr'] = data['work_yr'].fillna(0)
data['work_manage'] = data['work_manage'].fillna(0)
data['work_type'] = data['work_type'].fillna(0)

data['edu_yr'] = data['edu_yr'].fillna(0)
data['edu_status'] = data['edu_status'].fillna(0)

data['s_work_type'] = data['s_work_type'].fillna(0)
data['s_work_status'] = data['s_work_status'].fillna(0)
data['s_political'] = data['s_political'].fillna(0)
data['s_hukou'] = data['s_hukou'].fillna(0)
data['s_income'] = data['s_income'].fillna(0)
data['s_birth'] = data['s_birth'].fillna(0)
data['s_edu'] = data['s_edu'].fillna(0)
data['s_work_exper'] = data['s_work_exper'].fillna(0)

data['minor_child'] = data['minor_child'].fillna(0)
data['marital_now'] = data['marital_now'].fillna(0)
data['marital_1st'] = data['marital_1st'].fillna(0)
data['social_neighbor']=data['social_neighbor'].fillna(0)
data['social_friend']=data['social_friend'].fillna(0)
data['hukou_loc']=data['hukou_loc'].fillna(1) #最少為1，表示戶口
data['family_income']=data['family_income'].fillna(66365) #刪除問題值後的平均值

特殊格式的信息也需要處理，例如跟時間有關的信息，可以化成對應方便處理的格式，以及對年齡進行分段處理：

data['survey_time'] = pd.to_datetime(data['survey_time'], format='%Y-%m-%d',
                                     errors='coerce')
#防止時間格式不同的報錯errors='coerce‘,格式不對就幅值NaN
data['survey_time'] = data['survey_time'].dt.year #僅僅是year，方便計算年齡
data['age'] = data['survey_time']-data['birth']

bins = [0,17,26,34,50,63,100]
data['age_bin'] = pd.cut(data['age'], bins, labels=[0,1,2,3,4,5])

還有就是對一些異常值的處理，例如在某些問題中不應該出現負數但是出現了負數，那麼就可以根據我們的直觀理解來進行處理：

# 對宗教進行處理
data.loc[data['religion'] < 0, 'religion'] = 1  # 1代表不信仰宗教
data.loc[data['religion_freq'] < 0, "religion_freq"] = 0  # 代表不參加
# 教育
data.loc[data['edu'] < 0, 'edu'] = 1  # 負數說明沒有接受過任何教育
data.loc[data['edu_status'] < 0 , 'edu_status'] = 0
data.loc[data['edu_yr']<0,'edu_yr'] = 0

# 收入
data.loc[data['income']<0,'income'] = 0 #認為無收入
#對‘政治面貌’處理
data.loc[data['political']<0,'political'] = 1 #認為是群眾
#對體重處理
data.loc[(data['weight_jin']<=80)&(data['height_cm']>=160),'weight_jin']= data['weight_jin']*2
data.loc[data['weight_jin']<=60,'weight_jin']= data['weight_jin']*2  #沒有60斤的成年人吧
#對身高處理
data.loc[data['height_cm']<130,'height_cm'] = 150 #成年人的實際情況
#對‘健康’處理
data.loc[data['health']<0,'health'] = 4 #認為是比較健康
data.loc[data['health_problem']<0,'health_problem'] = 4  # 4代表很少
#對‘沮喪’處理
data.loc[data['depression']<0,'depression'] = 4 #很少
#對‘媒體’處理
data.loc[data['media_1']<0,'media_1'] = 1 #都是從不
data.loc[data['media_2']<0,'media_2'] = 1
data.loc[data['media_3']<0,'media_3'] = 1
data.loc[data['media_4']<0,'media_4'] = 1
data.loc[data['media_5']<0,'media_5'] = 1
data.loc[data['media_6']<0,'media_6'] = 1

#對‘空閑活動’處理
data.loc[data['leisure_1']<0,'leisure_1'] = data['leisure_1'].mode()  # 眾數
data.loc[data['leisure_2']<0,'leisure_2'] = data['leisure_2'].mode()
data.loc[data['leisure_3']<0,'leisure_3'] = data['leisure_3'].mode()
data.loc[data['leisure_4']<0,'leisure_4']