GreatSQL社區原創內容未經授權不得隨意使用,轉載請聯繫小編並註明來源。 GreatSQL是MySQL的國產分支版本,使用上與MySQL一致。 前文回顧 實現一個簡單的Database1(譯文) 實現一個簡單的Database2(譯文) 實現一個簡單的Database3(譯文) 實現一個簡單的D ...
- GreatSQL社區原創內容未經授權不得隨意使用,轉載請聯繫小編並註明來源。
- GreatSQL是MySQL的國產分支版本,使用上與MySQL一致。
前文回顧
譯註:cstsck在github維護了一個簡單的、類似sqlite的資料庫實現,通過這個簡單的項目,可以很好的理解資料庫是如何運行的。本文是第七篇,主要是對B-tree的介紹
Part 7 B-Tree簡介
B-tree是SQLite用來表示表和索引的數據結構,所以B-tree是非常中心的想法。這個主題主要是介紹B-tree數據結構,所以不會有任何的代碼。
為什麼說對於資料庫來說,樹是非常好的數據結構呢?
- 查找特定的value很快(對數時間花銷,loga N)
- 插入一行或者對查詢到的數據刪除很快(再平衡使用常量時間)
- 遍歷一個範圍內的value很快(不像hash map)
B-tree不同於二叉樹(“B”可能代表發明人的名字,但也可以代表“Balanced”)。這裡是一個B-tree例子:
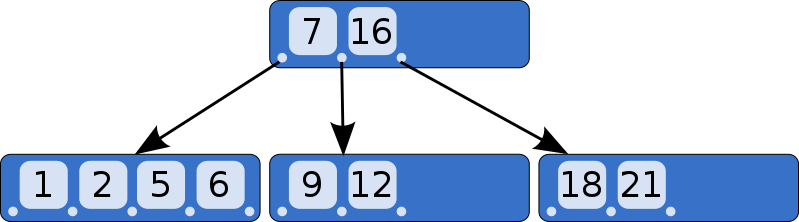
B-Tree 例子(https://en.wikipedia.org/wiki/File:B-tree.svg)
不像二叉樹每個節點只能有兩個子節點,B-tree的每個節點可以有兩個以上的子節點。每個節點最多可以有 m 個子節點,其中 m 叫做樹的“order”(或者叫“階”)。為了保持樹的儘量平衡,我們還要求節點必須至少有 m / 2 個子節點(四捨五入)。
但還有一些例外:
- 葉子節點沒有子節點
- 根節點的子節點數可以少於 m,但至少要有兩個
- 如果根節點也是葉子節點(樹只有一個節點),那它有0個子節點
上面的描述的是一個B-tree,SQLite用它來存儲索引。為了存儲表數據,SQLites使用一種B-tree的變體,稱為B+tree。
| B-tree | B+ tree | |
|---|---|---|
| 發音 | “Bee Tree” | “Bee Plus Tree” |
| 用來存儲 | 索引 | 表 |
| 內部節點是否存儲key | 是 | 是 |
| 內部節點是否存儲value | 是 | 否 |
| 每個節點的子節點數 | 少 | 多 |
| 內部節點 vs 葉子節點 | 相同結構 | 不同結構 |
在我們開始實現索引之前,我將只討論B+tree,但這裡將其稱為 B-tree 或者 btree。
有子節點(children)的節點被稱為“內部”節點(internal node),內部節點和葉子節點在結構上不同:
| m階tree | 內部節點 | 葉子節點 |
|---|---|---|
| 存儲 | key和指向子節點的指針 | key和value |
| key的數目 | 最多m-1個 | 越多越好 |
| 指針的數目 | keys + 1 | 無 |
| value的數目 | 無 | 與key的數目相同 |
| Key的用途 | 用來路由 | 與value成對存儲 |
| 存儲value? | 否 | 是 |
這裡通過一個例子來看一下,當插入一個元素時,B-tree是怎樣發生結構變化的。為了讓事情看起來更容易理解,這棵B-tree的階(order)設置為3(m=3),也就是說:
- 每個內部節點最多有三個子節點(m)
- 每個內部節點最多有兩個key
- 每個內部節點至少兩個子節點(m-1)
- 每個內部節點至少一個key
一棵空樹只有一個節點:根節點。根節點最開始也作為葉子節點,有0個鍵值對(key/value):
空的btree
如果我們插入兩個鍵值對(超過兩個鍵值對,節點需要分裂,參考上面規則),他們會按順序排序存放在葉子節點中。
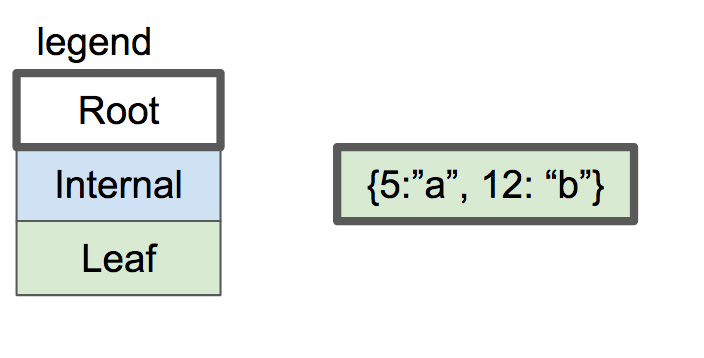
一個節點的btree
我們假設了節點的容量是兩個鍵值對兒。當我們插入另外一個的時候,就不得不分裂葉子節點了,分裂後的兩個節點每個存放之前一半的鍵值對。分裂後的兩個節點都變成了內部節點,同時也變成了一個新的節點的子節點,這個新的節點變成了根節點。
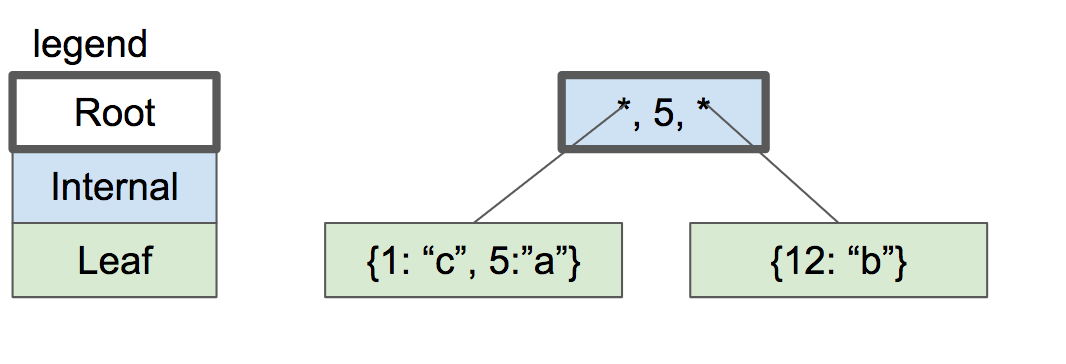
兩層的btree
圖中的內部節點(也是根節點)有一個key和兩個指針指向子節點(就是那兩條線)。如果我們想查找一個key,key小於或等於5,我們查看左子樹。如果查找的key大於5,就查看右子樹。
現在,準備插入一個新的key "2"。首先,我們查找它將位於哪個葉節點(如果它在樹中存在的話),這樣就到達了左側葉子節點。這個節點是滿的,所以把這個葉子節點進行分裂(split),併在父節點創建新的條目。
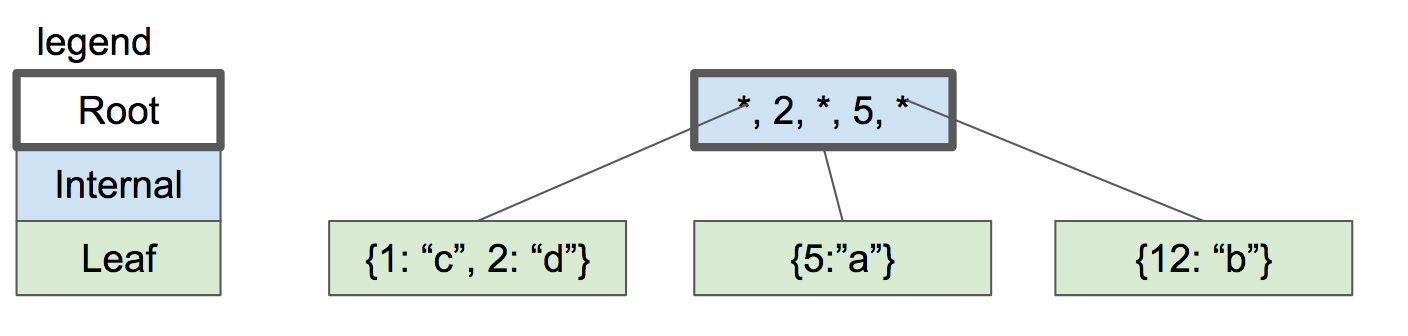
四節點的btree
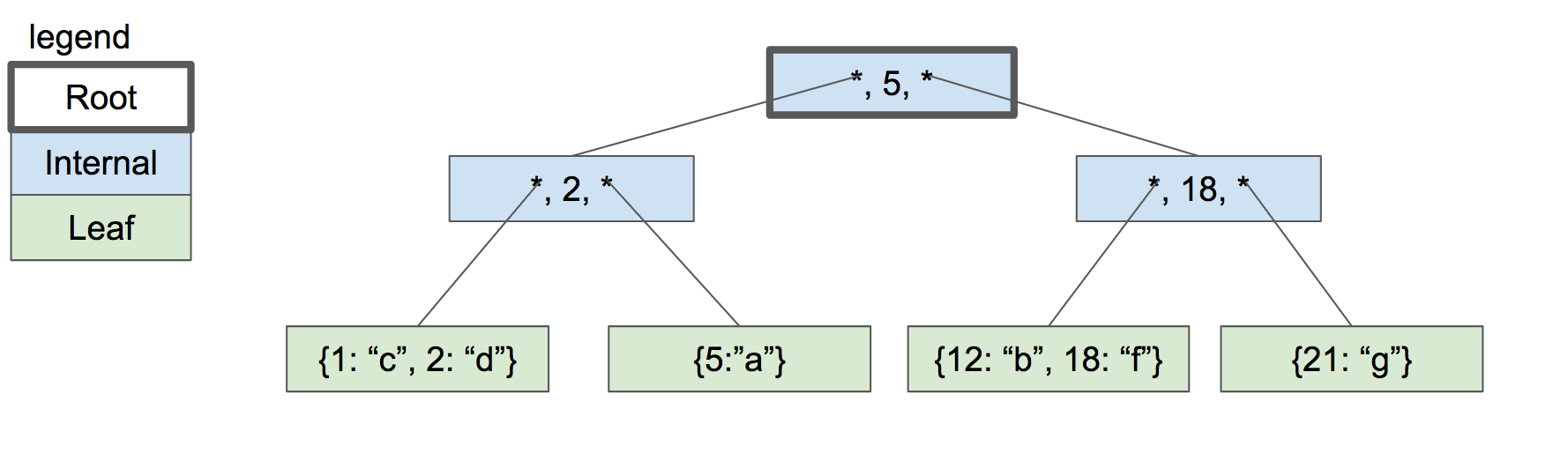
現在繼續增加key,18 和 21 。現在又到了不得不分裂的情況,但是在父節點中已經沒有空間來增加新的鍵值對兒了。
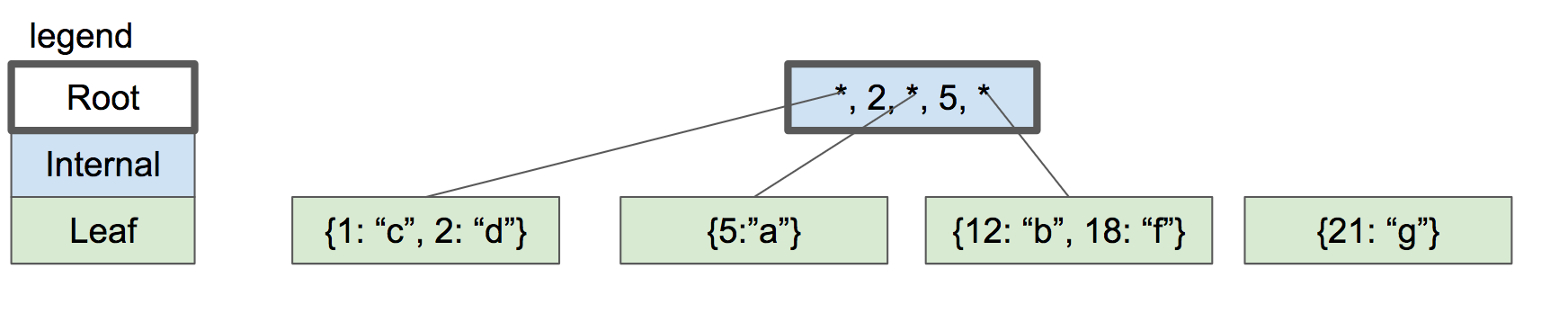
內部節點沒有空間
解決方法就是分裂根節點為兩個內部節點,然後創建一個新的根節點作為兩個內部節點的父節點。

三層的btree
樹只是在我們分裂根節點的時候才會增加深度。每個葉子節點都有相同的深度和接近相同的數量的鍵值對兒,所以樹能夠保持平衡和快速的進行查找。
我暫時先不討論從樹中刪除鍵的操作,推遲到實現插入操作以後。
當我們實現這個數據結構時,每個節點都對應一個page。根節點將在page0中存在。節點中的子節點指針將簡單的使用包含子節點的page number。
下一次,我們開始實現btree。
Enjoy GreatSQL



