R語言之旅。原書P88頁案例3-3解答。根據描述統計量有什麼見解、本國學生和國外學生學費差別、工作經驗要求與否與起薪差別、英語測試要求與否與起薪差別、起薪與學費關係。 ...
-
編程教材 《R語言實戰·第2版》Robert I. Kabacoff
-
課程教材《商務與經濟統計·原書第13版》 (安德森)
P86、案例3-3 亞太地區商學院

載入數據
已知數據集為csv文件,所以要按間隔符形式導入。並刪除帶預設值的列。
- 字元串替換函數 gsub(匹配內容,替換內容,操作對象)
- 類型轉換函數 as.numeric
# ^ 載入數據並刪除帶預設值的列。
Asian <- read.table("./data/Asian.csv",
header = TRUE, sep = ","
)
# row.names = "Business.School",
res1 <- data.frame(Asian)
library(dplyr)
Asian <- res1 %>% select_if(~ !any(is.na(.)))
# ^ 數值字元串類型數據轉數值類型數據
Asian$Local.Tuition.... <- gsub(",", "", Asian$Local.Tuition....)
Asian$Foreign.Tuitiion.... <- gsub(",", "", Asian$Foreign.Tuitiion....)
Asian$Starting.Salary.... <- gsub(",", "", Asian$Starting.Salary....)
Asian$Local.Tuition.... <- as.numeric(Asian$Local.Tuition....)
Asian$Foreign.Tuitiion.... <- as.numeric(Asian$Foreign.Tuitiion....)
Asian$Starting.Salary.... <- as.numeric(Asian$Starting.Salary....)
# ^ 描述性統計
print(summary(Asian))
View(Asian)
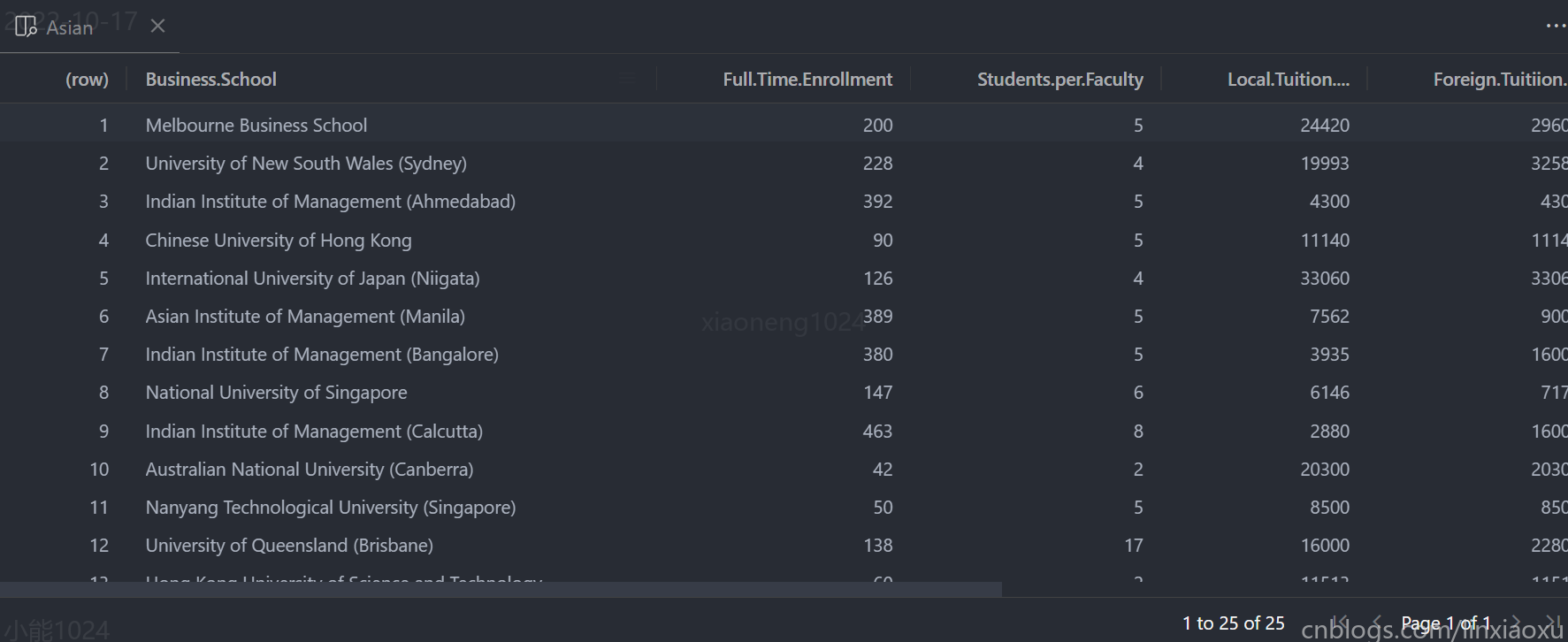
根據描述統計量有什麼見解
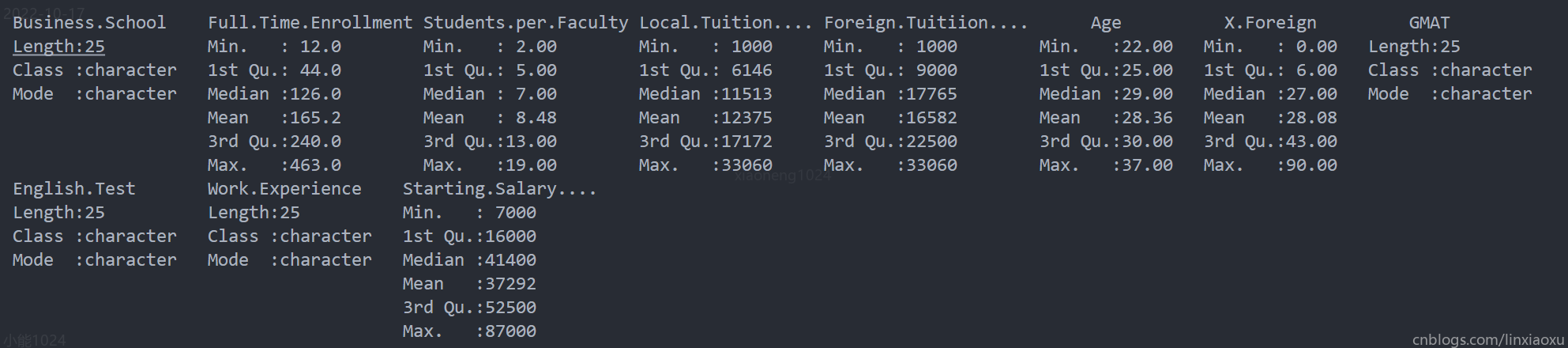
- 總共有25所商學院,每所商學院平均錄取165人。最多錄取數量商學院為印度管理學院,錄取463人。最少錄取數量商學院為麥誇里管理研究生院,錄取12人。不同學校之間錄取名額差異較大。
- 所有商學院每個學院人數平均8人,最多的學院人數為19人,最少的學院人數為2人。可能部分商學院開設的學院數量比較多,有的比較少。
- 本國學生平均學費為12375美元,外國學生平均學費16582美元。本國、外國學生最低學費和最高學費相同,分別是1000美元和33060美元。外國學生平均學費要比本國學生平均學費高一點。
- 不同商學院國外學生平均比例為28%,最多國外學生占比為90%,最少國外學生占比為0%。可能部分商學院知名度比較高或者是國外學生錄取門檻較低。
- 不同商學院平均起薪為37292美元,最少起薪7000美元,最高起薪為87000美元。
本國學生和國外學生學費差別
# ^ 本國學生和國外學生學費差別
library(tidyverse)
data1 <- data.frame(Type = "Loacal", Tuition = Asian$Local.Tuition...., School = Asian$Business.School)
data2 <- data.frame(Type = "Foreign", Tuition = Asian$Foreign.Tuitiion...., School = Asian$Business.School)
data <- rbind(data1, data2)
x11()
ggplot(data, aes(x = School, y = Tuition, color = Type, shape = Type)) +
geom_point(size = 3) +
geom_line(mapping = aes(y = Tuition, group = Type, color = Type), stat = "identity", size = 1.3) +
labs(x = "School", y = "Tuition") +
scale_y_continuous(breaks = c(5000, 10000, 15000, 20000, 25000, 30000, 35000, 40000), limits = c(0, 40000)) +
geom_hline(aes(yintercept = 0)) + # 加入一條平行於x軸的線,透明度(alpha)調成了65%
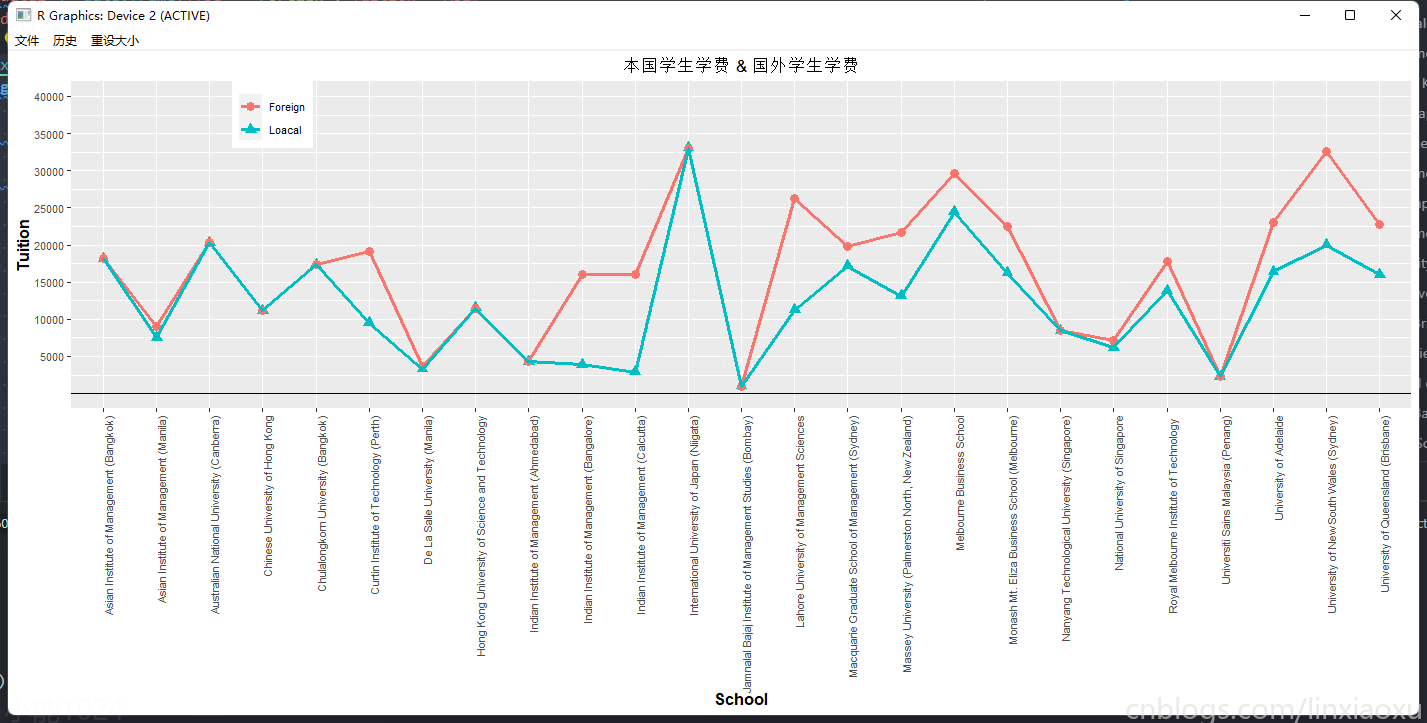
ggtitle("本國學生學費 & 國外學生學費") +
theme(
axis.text.x = element_text(angle = 90, hjust = 1), # 把x軸標簽調整為90度
legend.title = element_blank(), # 設置圖例標題為空
legend.position = c(0.15, 0.9), # 設置圖例的位置在左上角
legend.text = element_text(size = 8), # 設置圖例的文字大小為10號
plot.caption = element_text(hjust = 0.5, size = 15), # 設置圖標題位置
axis.text = element_text(size = 8), # 設置圖例的文字大小
axis.title = element_text(size = 12, face = "bold"), # 設置軸標題文字大小和文字加粗
plot.title = element_text(hjust = 0.5) # 標題文字居中
)
Local.Tuition.... Foreign.Tuitiion....
Min. : 1000 Min. : 1000
1st Qu.: 6146 1st Qu.: 9000
Median :11513 Median :17765
Mean :12375 Mean :16582
3rd Qu.:17172 3rd Qu.:22500
Max. :33060 Max. :33060
結合折線圖和五數概括法可知
-
本國學生平均學費為12375美元,外國學生平均學費16582美元。本國、外國學生最低學費和最高學費相同,分別是1000美元和33060美元。
-
國外學生學費比本國學生學費要高。本國學生學費第一、二、三四分位數都比國外學生學費高。
工作經驗要求與否與起薪差別
# ^ 工作經驗與起薪的差別
b <- aggregate(
x = Asian$Starting.Salary...., # @ 聚合變數
by = list(Asian$Work.Experience), # @ 分組依據
FUN = summary, # @ 聚合函數
)
print(b)
Group.1 x.Min. x.1st Qu. x.Median x.Mean x.3rd Qu. x.Max.
1 No 7100.00 7425.00 7500.00 24583.33 25125.00 87000.00
2 Yes 7000.00 23900.00 46600.00 41305.26 53750.00 71400.00
通過五數概括法,可知不要求工作經驗的平均起薪24583.33美元,要求工作經驗的平均起薪41305美元,比前者要來得高。
英語測試要求與否與起薪差別
# ^ 工作經驗與起薪的差別
c <- aggregate(
x = Asian$Starting.Salary...., # @ 聚合變數
by = list(Asian$English.Test), # @ 分組依據
FUN = summary, # @ 聚合函數
)
print(c)
Group.1 x.Min. x.1st Qu. x.Median x.Mean x.3rd Qu. x.Max.
1 No 7000.00 7500.00 31000.00 33623.53 55000.00 71400.00
2 Yes 16000.00 37300.00 44950.00 45087.50 49800.00 87000.00
通過五數概括法,可知
-
不要求英語測試的最低起薪為7000美元,要求英語測試的最低起薪為16000美元。
-
不要求英語測試的平均起薪為33623美元,要求工作經驗的平均起薪45087美元,比前者要來得高。
-
不要求英語測試的起薪第一、二四分位數比要求英語測試的第一、二四分位數低,但不要求英語測試的起薪第三四分位數(55000)卻比要求英語測試的第三四分位數(49800)高。
起薪與學費關係
# ^ 起薪與學費關係的散點圖
png(file = "Asian_scatterplot_1.png")
plot(
x = Asian$Starting.Salary...., y = Asian$Local.Tuition....,
xlab = "起薪",
ylab = "本國學生學費",
xlim = c(6000, 88000),
ylim = c(0, 31000),
main = "起薪與本國學生學費關係的散點圖"
)
# ^ ?~? 符號相當於 y~x
m1 <- lm(Local.Tuition.... ~ Starting.Salary...., data = Asian) # @ 建立回歸模型
abline(m1, lwd = 3, col = "darkorange")
dev.off()
png(file = "Asian_scatterplot_2.png")
plot(
x = Asian$Starting.Salary...., y = Asian$Foreign.Tuitiion....,
xlab = "起薪",
ylab = "外國學生學費",
xlim = c(6000, 88000),
ylim = c(0, 31000),
main = "起薪與外國學生學費關係的散點圖"
)
m2 <- lm(Foreign.Tuitiion.... ~ Starting.Salary...., data = Asian) # @ 建立回歸模型
abline(m2, lwd = 3, col = "darkorange")
dev.off()
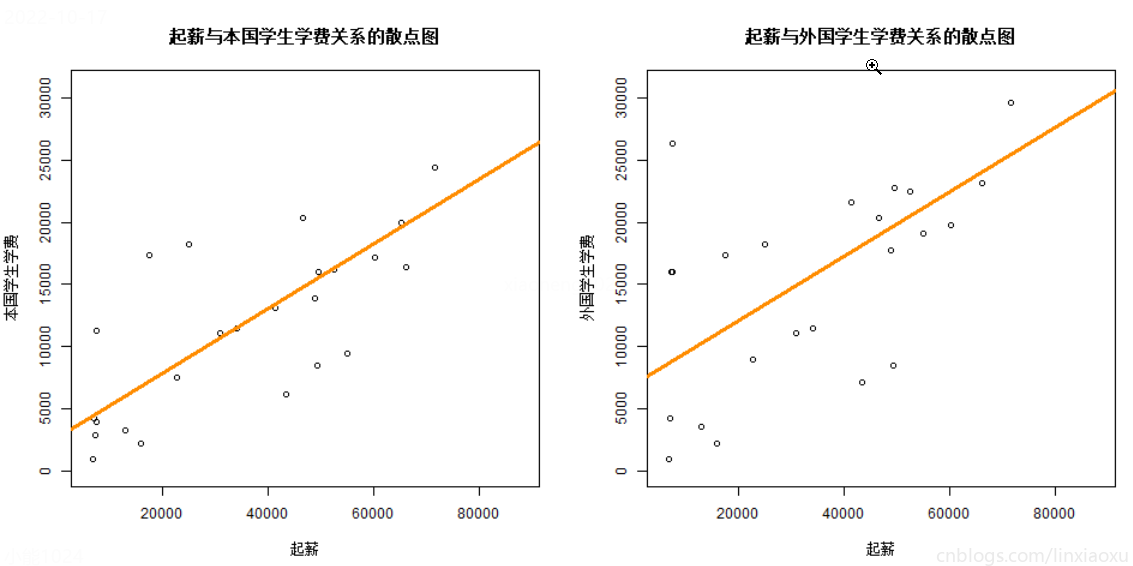
從兩幅圖中可知,學生學費和起薪呈正相關,本國學生學費和起薪的相關係數為0.79,外國學生學費和起薪的相關係數為0.67。
其他圖形-起薪頻率分組
# ^起薪頻率分組
typeTable3 <- within(Asian, {
group1 <- NA
group1[Starting.Salary.... >= 7000 & Starting.Salary.... < 23000] <- "[7000~23000)"
group1[Starting.Salary.... >= 23000 & Starting.Salary.... < 39000] <- "[23000~39000)"
group1[Starting.Salary.... >= 39000 & Starting.Salary.... < 55000] <- "[39000~55000)"
group1[Starting.Salary.... >= 55000 & Starting.Salary.... < 71000] <- "[55000~71000)"
group1[Starting.Salary.... >= 71000 & Starting.Salary.... <= 87000] <- "[71000~87000]"
})
typeTable4 <- table(typeTable3$group1)
typeTable4 <- prop.table(typeTable4) * 100
# @ 預設按字元串排序,重新排列表格列
typeTable4 <- typeTable4[c(4, 1, 2, 3, 5)]
print(as.data.frame(typeTable4))
png(file = "Asian_barplot.png")
par(mar = c(10, 4, 4, 0))
barplot(typeTable4,
main = "起薪頻率分組條形圖",
xlab = "", ylab = "頻率", las = 2, col = rainbow(25)
)
dev.off()
Var1 Freq
1 [7000~23000) 36
2 [23000~39000) 12
3 [39000~55000) 28
4 [55000~71000) 16
5 [71000~87000] 8
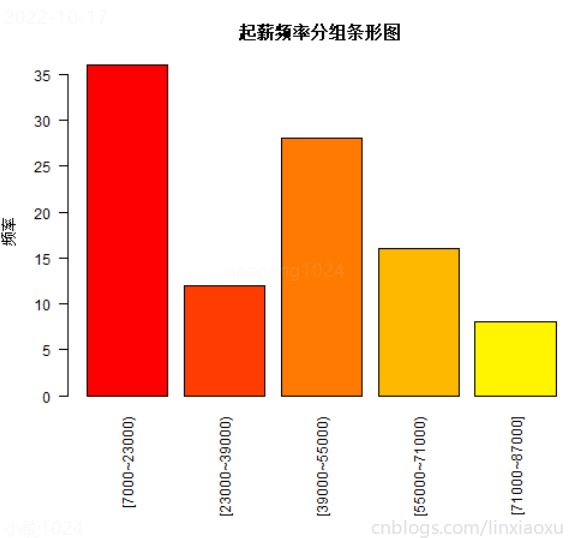
從圖中可知起薪分組頻率分佈形態適度右偏。[7000~23000)區間薪水居多,其次是是[39000~55000]區間。



