機器學習實戰-Logistic回歸_ZenDei技術網路在線

1.基於 Logistic 回歸和 Sigmoid 函數的分類邏輯回歸適合於01情況的分類就是描述一個問題是或者不是，所以就引入sigmoid函數，因為這個函數可以將所有值變成0-1之間的一個值，這樣就方便算概率首先我們可以先看看Sigmoid函數(又叫Logistic函數)將任意的輸入映射到了 ...

1.基於 Logistic 回歸和 Sigmoid 函數的分類

邏輯回歸適合於01情況的分類就是描述一個問題是或者不是，所以就引入sigmoid函數，因為這個函數可以將所有值變成0-1之間的一個值，這樣就方便算概率首先我們可以先看看Sigmoid函數(又叫Logistic函數)將任意的輸入映射到了[0,1]區間我們線上性回歸中可以得到一個預測值，再將該值映射到sigmoid函數中這樣就完成了由值到概率的轉換，也就是分類任務，公式如下：

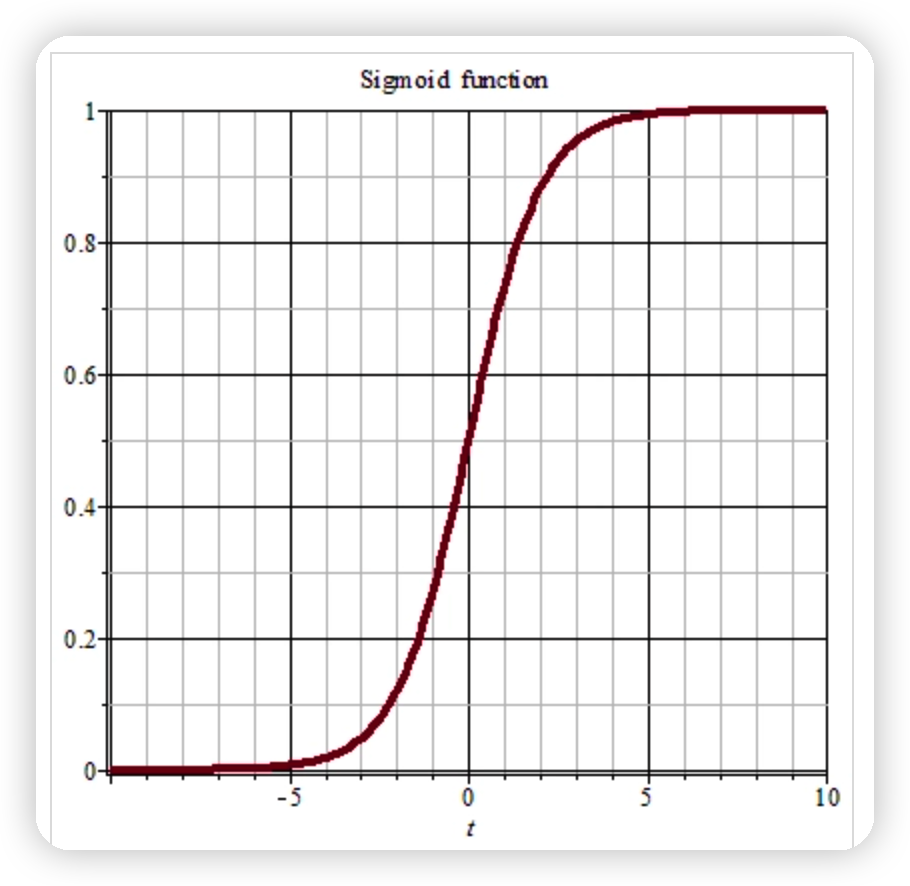
整合成一個公式，就變成瞭如下公式：

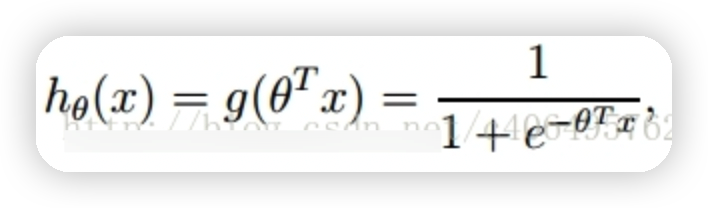
z是一個矩陣，θ是參數列向量(要求解的)，x是樣本列向量(給定的數據集)，θ^T表示θ的轉置

Sigmoid函數的輸入記為z，由下麵公式得出:
z=w0x0+w1x1+w2x2+...+wnxn
如果採用向量的寫法，上述公式可以寫成z = wTx，它表示將這兩個數值向量對應元素相乘然後
全部加起來即得到z值。其中的向量x是分類器的輸入數據，向量w也就是我們要找到的最佳參數 (繫數)，從而使得分類器儘可能地精確。

邏輯回歸的簡單來說，就是根據數據得到的回歸直線方程z=a*x+b方程之後，將z作為sigmoid的輸入使得z的值轉化為在0-1之間的值，然後計算概率，最後根據sigmod函數的特點也就是當輸入為零的時候，函數值為0.5，以0.5為分界線來劃分數據的類型。

1.1梯度上升法

梯度上升演算法用來求函數的最大值，而梯度下降演算法用來求函數的最小值。
求一個函數的最大值，在數學中，是不是通過對函數求導，然後算出導數等於0，或者導數不存在的位置作為極值，然後如果極值只有一個開區間內是不是極值就是最大值。但是在實際應用中卻不是這麼簡單的去求最大值，而是通過迭代的方式一步一步向最值點靠近，最後得到最值。這也就是梯度上升法的思想

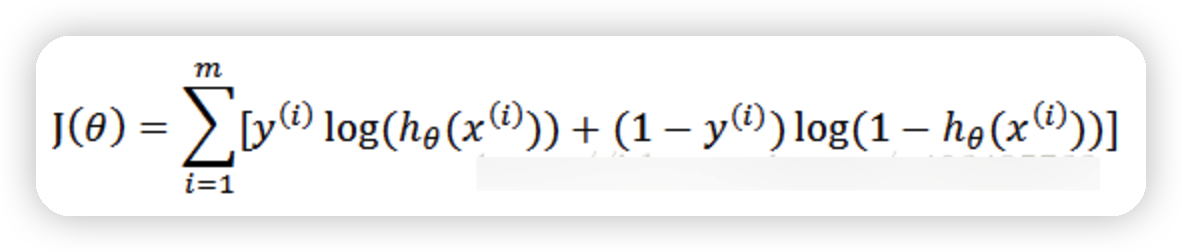
其中，m為樣本的總數，y(i)表示第i個樣本的類別，x(i)表示第i個樣本，需要註意的是θ是多維向量，x(i)也是多維向量。

梯度上升迭代公式為：

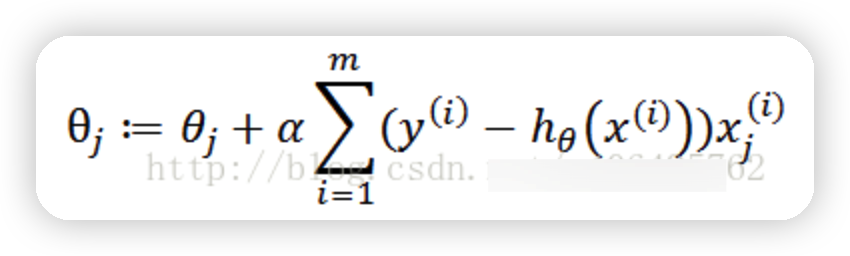
代碼實現：

import matplotlib.pyplot as plt
import numpy as np
import warnings
warnings.filterwarnings('ignore')

def loadDataSet():
    dataMat = []   #創建數據列表
    labelMat = []   #創建標簽列表
    fr = open('testSet.txt')    #打開文件
    for line in fr.readlines():     #逐行讀取
        lineArr = line.strip().split()  #去回車，放入列表
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #添加數據
        labelMat.append(int(lineArr[2]))   #添加標簽
    fr.close()   #關閉文件
    return dataMat, labelMat    #返回


def sigmoid(inX):
    return  1.0/(1+np.exp(-inX))

#dataMatIn，它是一個2維NumPy數組，每列分別代表每個不同的特征,每行則代表每個訓練樣本
def gradAscent(dataMatIn,classLabels):
    dataMatrix=np.mat(dataMatIn)#轉換成numpy的mat
    labelMat=np.mat(classLabels).transpose()#為了便於矩陣運算，需要將該行向量轉換為列向量，做法是將原向量轉置，再將它賦值給labelMat
    m,n=np.shape(dataMatrix) #返回dataMatrix的大小。m為行數,n為列數。
    alpha=0.001 #向目標移動的步長
    maxCycles=500 #maxCycles是迭代次數
    weights=np.ones((n,1))#權重初始化都為1
    for k in range(maxCycles):
        h=sigmoid(dataMatrix*weights)#梯度上升矢量化公式
        error=(labelMat-h)#相當於公式中的y(i)-h(x(i))
        weights=weights+alpha*dataMatrix.transpose()*error#公式裡面的累加在這裡使用矩陣相乘來實現(矩陣相乘的過程中先乘再加)
    return weights.getA()  #返回權重數組


def plotBestFit(weights):
    dataMat, labelMat = loadDataSet() #載入數據集
    dataArr = np.array(dataMat) #轉換成numpy的array數組
    n = np.shape(dataMat)[0]  #數據個數
    xcord1 = []; ycord1 = []   #正樣本
    xcord2 = []; ycord2 = []   #負樣本
    for i in range(n):    #根據數據集標簽進行分類
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2]) #1為正樣本
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])#0為負樣本
    fig = plt.figure()
    ax = fig.add_subplot(111) #添加subplot
    ax.scatter(xcord1, ycord1, s = 20, c = 'red', marker = 's',alpha=.5)#繪製正樣本
    ax.scatter(xcord2, ycord2, s = 20, c = 'green',alpha=.5)  #繪製負樣本
    x = np.arange(-3.0, 3.0, 0.1)
    y = (-weights[0] - weights[1] * x) / weights[2]
    ax.plot(x, y)
    plt.title('BestFit')  #繪製title
    plt.xlabel('X1'); plt.ylabel('X2') #繪製label
    plt.show()

if __name__ == '__main__':
    dataMat, labelMat = loadDataSet()
    weights = gradAscent(dataMat, labelMat)
    plotBestFit(weights)
    #plotDataSet()

正常運行之前報瞭如下錯誤AttributeError: partially initialized module ‘matplotlib.cbook’ has no attribute ‘deprecated’ (most likely due to a circular import)

然後就是你安裝的matplotlib版本太高了，可以將以前的版本給卸載了，然後安裝一個版本較低的matplotlib，然後就可以解決

測試結果

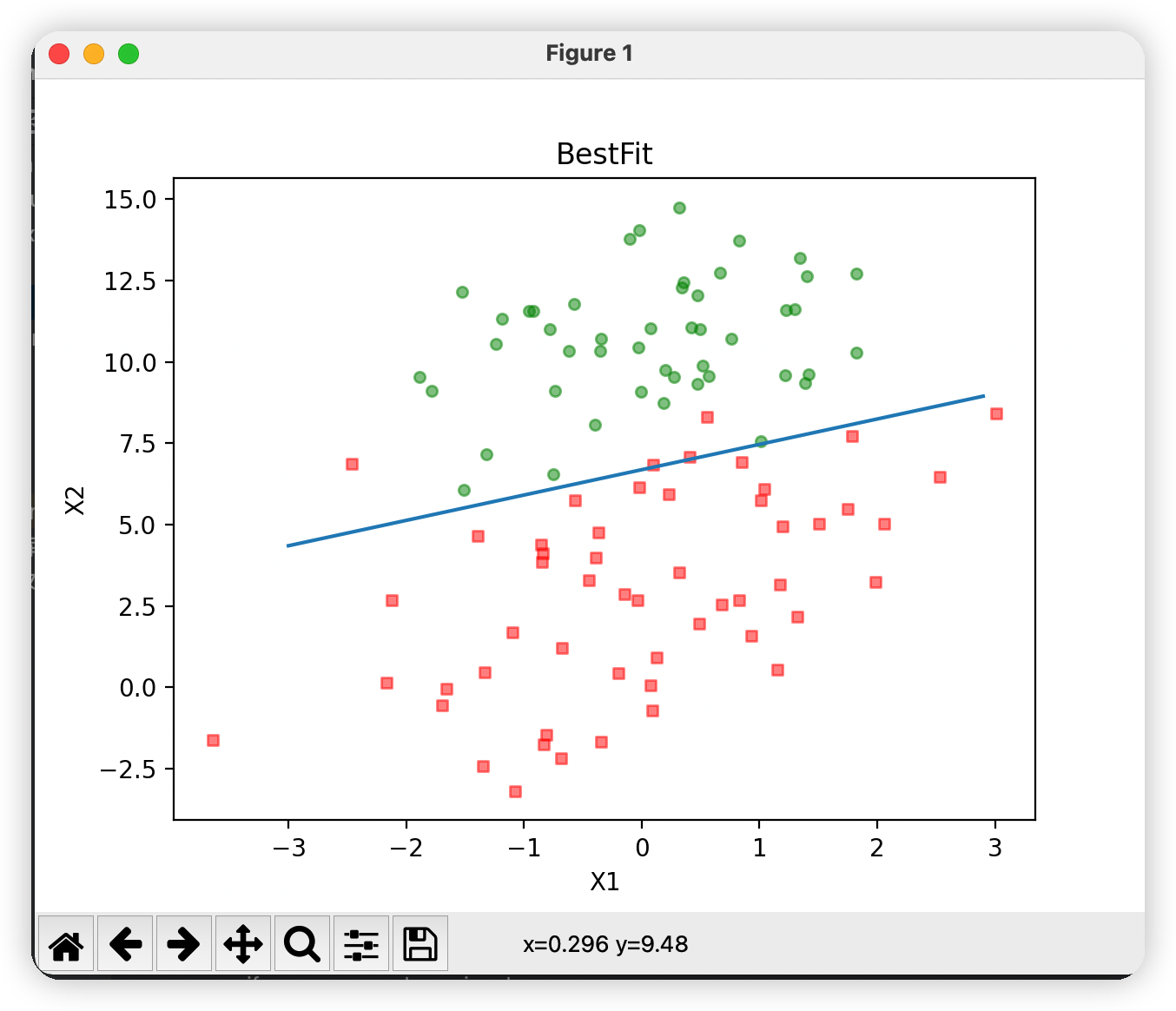
總結：代碼運行的大致思路如下：

拿到數據之後通過loadDataSet函數將數據的坐標和類別分別存放在兩個數組中
然後通過拿到的坐標數組和分類數組，首先先將數組轉換為矩陣，方便後面矩陣的運算，然後根據sigmoid函數將所有數據轉化為0-1之間的數據，也即公式中的h(xi)的值，然後用每個樣本的類標簽減去梯度上升的矢量值，最後帶入公式算出當前的權重值
繪圖
- 然後繪圖的時候定義兩種數據類型的x坐標的數組和對應的y坐標的數組，然後通過數據集，將每種類別對應的x坐標和y坐標分開存入對應的數組中
- 然後繪製一張空的面板，添加坐標系，然後將每個同一類別的點畫在面板上，並且同一類別的點的顏色相同
- 最後畫擬合的直線，橫坐標的範圍已知，然後取sigmoid 函數為0。0是兩個分類(類別1和類別0)的分界處。因此，我們設定 0 = w0x0 + w1x1 + w2x2，然後解出X2和X1的關係式(即分隔線的方程，註意X0=1)。
- 最後根據函數方程和x的值將直線畫在面板上即可

1.2改進的梯度上升演算法

改進的第一點也就是改變每次向目標點靠近的步長的值，最初的時候也能稍微大點，然後隨著迭代次數的增加，也就是離目標點越來越近，此時每次向前的步長也越來越小；第二點就是樣本的選取也是隨機的；第三點就是原來計算出來的h是一個100乘以1的矩陣，而現在算出來的是一個0-1之間的數值；第四點就是原來計算回歸繫數的時候使用一個3*100的矩陣乘以一個100*1的一個矩陣，現在是三個數值的乘積

#改進的梯度上升演算法
#迭代次數150是根據上面的代碼測試出來的
def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = np.shape(dataMatrix)  #返回dataMatrix的大小。m為行數,n為列數。
    weights = np.ones(n)   #參數初始化
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01  #降低alpha的大小，每次減小1/(j+i)。
            randIndex = int(random.uniform(0,len(dataIndex)))  #隨機選取樣本
            h = sigmoid(sum(dataMatrix[randIndex]*weights)) #選擇隨機選取的一個樣本，計算h
            error = classLabels[randIndex] - h   #計算誤差
            weights = weights + alpha * error * dataMatrix[randIndex]  #更新回歸繫數
            del(dataIndex[randIndex])  #刪除已經使用的樣本
    return weights

1.3回歸繫數與迭代次數的關係

#2.為改進之前查看回歸繫數與迭代次數的關係
def gradAscent1(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)   #轉換成numpy的mat
    labelMat = np.mat(classLabels).transpose()  #轉換成numpy的mat,併進行轉置
    m, n = np.shape(dataMatrix)    #返回dataMatrix的大小。m為行數,n為列數。
    alpha = 0.01  #移動步長,也就是學習速率,控制更新的幅度。
    maxCycles = 500    #最大迭代次數
    weights = np.ones((n,1))
    weights_array = np.array([])
    for k in range(maxCycles):
        h = sigmoid(dataMatrix * weights)  #梯度上升矢量化公式
        error = labelMat - h
        weights = weights + alpha * dataMatrix.transpose() * error
        weights_array = np.append(weights_array,weights)
    weights_array = weights_array.reshape(maxCycles,n)
    return weights.getA(),weights_array #將矩陣轉換為數組，並返回

#改進之後的
def stocGradAscent(dataMatrix, classLabels, numIter=150):
    m,n = np.shape(dataMatrix)                                                #返回dataMatrix的大小。m為行數,n為列數。
    weights = np.ones(n)                                                       #參數初始化
    weights_array = np.array([])                                            #存儲每次更新的回歸繫數
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01                                            #降低alpha的大小，每次減小1/(j+i)。
            randIndex = int(random.uniform(0,len(dataIndex)))                #隨機選取樣本
            h = sigmoid(sum(dataMatrix[randIndex]*weights))                    #選擇隨機選取的一個樣本，計算h
            error = classLabels[randIndex] - h                                 #計算誤差
            weights = weights + alpha * error * dataMatrix[randIndex]       #更新回歸繫數
            weights_array = np.append(weights_array,weights,axis=0)         #添加回歸繫數到數組中
            del(dataIndex[randIndex])                                         #刪除已經使用的樣本
    weights_array = weights_array.reshape(numIter*m,n)                         #改變維度
    return weights,weights_array

測試結果

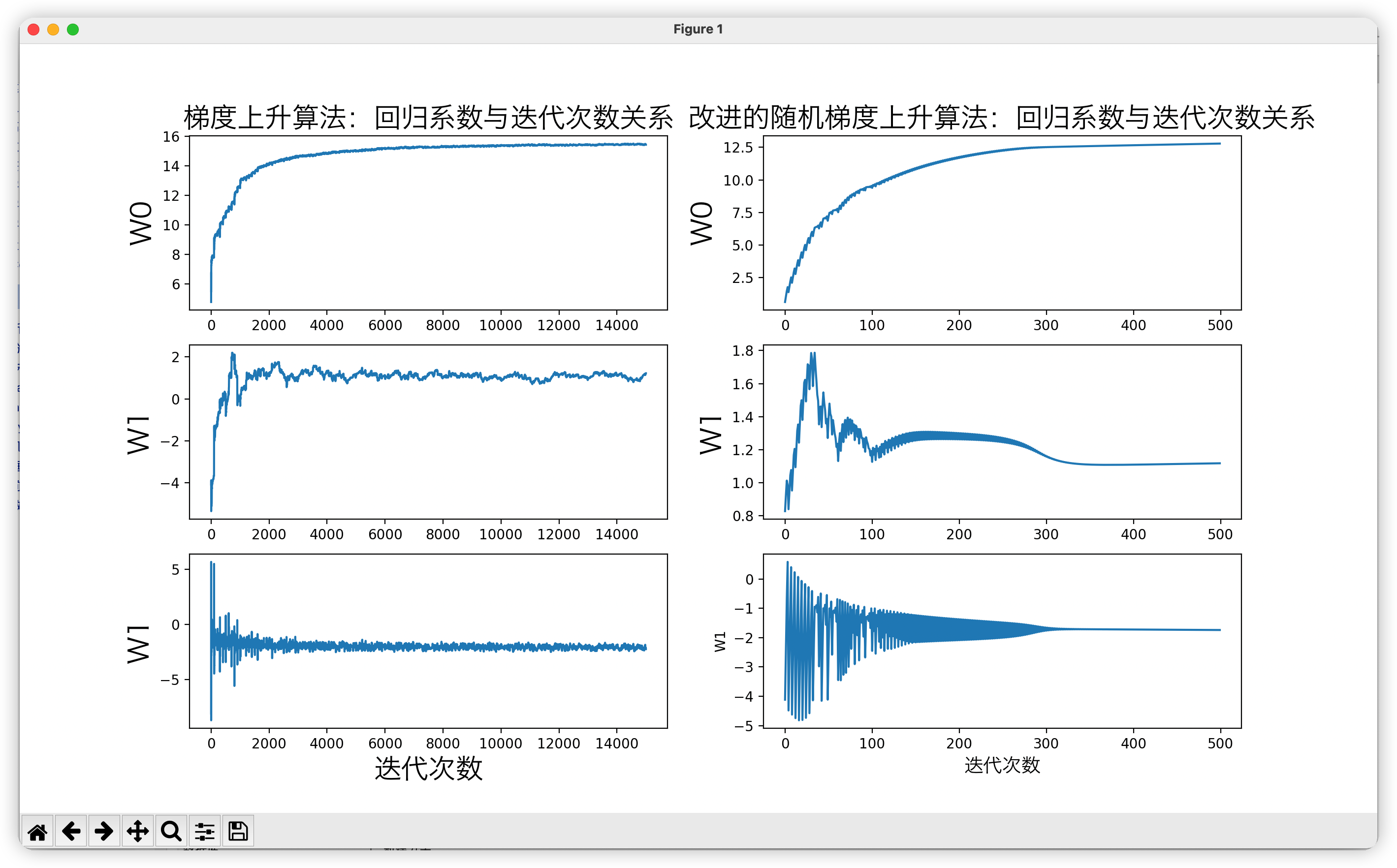
讓我們分析一下。我們一共有100個樣本點，改進的隨機梯度上升演算法迭代次數為150。而上圖顯示15000次迭代次數的原因是，使用一次樣本就更新一下回歸繫數。因此，迭代150次，相當於更新回歸繫數150*100=15000次。簡而言之，迭代150次，更新1.5萬次回歸參數。從上圖左側的改進隨機梯度上升演算法回歸效果中可以看出，其實在更新2000次回歸繫數的時候，已經收斂了。相當於遍歷整個數據集20次的時候，回歸繫數已收斂。訓練已完成。

上圖右側的梯度上升演算法回歸效果，梯度上升演算法每次更新回歸繫數都要遍歷整個數據集。從圖中可以看出，當迭代次數為300多次的時候，回歸繫數才收斂。湊個整，就當它在遍歷整個數據集300次的時候已經收斂好了。

2.從疝氣病癥狀預測病馬的死亡率

代碼實現

def classifyVector(inX, weights):
    prob = sigmoid(sum(inX*weights))
    if prob > 0.5: return 1.0
    else: return 0.0

def colicSklearn():
    frTrain = open('horseColicTraining.txt')  #打開訓練集
    frTest = open('horseColicTest.txt') #打開測試集
    trainingSet = []; trainingLabels = []
    testSet = []; testLabels = []
    for line in frTrain.readlines():#取出訓練集中的每一行的所有數據
        currLine = line.strip().split('\t')#每一行里數據的劃分以空格劃分
        lineArr = []
        for i in range(len(currLine)-1):#遍歷每一行的每個元素
            lineArr.append(float(currLine[i]))#lineArr里存放的就是每一行中所有的數據
        trainingSet.append(lineArr)#將每一行的數據存放在訓練集中
        trainingLabels.append(float(currLine[-1]))#拿到每一行的最後一列也即數據類別
    for line in frTest.readlines():#取出測試集中每一行的所有數據
        currLine = line.strip().split('\t')
        lineArr =[]
        for i in range(len(currLine)-1):
            lineArr.append(float(currLine[i]))
        testSet.append(lineArr)
        testLabels.append(float(currLine[-1]))
    classifier = LogisticRegression(solver='liblinear',max_iter=10).fit(trainingSet, trainingLabels)
    test_accurcy = classifier.score(testSet, testLabels) * 100
    print('正確率:%f%%' % test_accurcy)

測試結果