目錄

1 如何更新權值向量？
2 最小均方法（LMS）與感知機：低效的民主
3 最小二乘法：完美的民主
4 支持向量機：現實的民主
5 總結
6 參考資料

1 如何更新權值向量？

　　在關於線性模型你可能還不知道的二三事（一、樣本）中我已提到如何由線性模型產生樣本，在此前提下，使用不同機器學習演算法來解決回歸問題的本質都是求解該線性模型的權值向量W。同時，我們常使用線性的方式來解決分類問題：求解分隔不同類別個體的超平面的法向量W。不論回歸還是分類，都是求解向量W，而求解的核心思想也英雄所見略同：向量W傾向於指向某些“重要”的個體。然而哪些個體是重要的呢？不同的機器學習演算法有不同的定義。

2 最小均方法（LMS）與感知機：低效的民主

　　最小均方法（LMS）使用的隨機梯度下降法與感知機的訓練法則類似，兩者都是迭代更新的方式。假設本次迭代中的權值為W，那麼更新後的權值W'為（eta為更新率）：

　　隨機梯度下降法：

　　感知機：

　　通過觀察可知，權值更新是一個迭代的過程，不論是回歸（最小均方法）還是分類（感知機），權值更新時視當前輪次中誤差大的個體為“重要”的個體。這種權值更新辦法比較直觀，但是同時也比較低效：人人都有發言的權利，每次只考慮部分人，容易顧此失彼。

3 最小二乘法：完美的民主

　　二乘即是平方，最小二乘法旨在於求解權值向量W使得誤差平方和最小：

　　通過對權值向量的每個分量進行求導可得：

　　至此，我們可以發現最小二乘法可解的條件為特征矩陣X是可逆的。假設特征矩陣X的樣本容量n=m，那麼上式進一步化簡得：

　　使用求解出來的權值向量W'對未知個體x'進行預測，本質就是計算：

　　在《關於線性模型你可能還不知道的二三事（一、樣本）》中我們已經揭開了特征矩陣X的逆矩陣的意義，因此以上的計算過程可以概括為：首先使用X的逆矩陣乘以未知個體x'，得到可以準確描述未知個體x'與特征矩陣X中已知個體相似度的列向量，然後以此為基礎，使用加權求和的方法來計算未知個體x'的目標值。

　　到此，最小二乘法所詮釋的完美民主已顯見：在每個人都不能由其他人代表的前提下，看未知的個體與誰更相似，那麼目標值也與之更相似。

　　沒錯，之前我們假設了特征矩陣X的樣本容量n=m，但是大多數情況下n是大於m的。這種情況下權值向量計算公式無法進一步化簡。同樣在《關於線性模型你可能還不知道的二三事（一、樣本）》中我們提到，可以轉化原問題為：

　　這時，我們可以設新的特征矩陣X'和新的目標值向量Y'為：

　　到此，新的特征矩陣X'是m×m的方陣，可以求其逆矩陣了（當然，這還是在原特征矩陣的秩等於m的前提下）。因此有：

　　不難看到，上式同樣也是詮釋了完美的民主，只是特征矩陣X變成了X'，目標值向量Y變成了Y'而已。

4 支持向量機：現實的民主

　　完美的民主可遇而不可求，如果特征矩陣X的秩小於m呢？此時最小二乘法便不奏效了。我們期望無論特征矩陣X的秩是否小於m，仍然可以高效地求解權值向量W。

　　我們可以利用支持向量機解決該問題。不妨直接看到權值向量的最終結果（具體推導可參考《支持向量機通俗導論（理解SVM的三層境界）》）：

　　使用上式計算出來的權值向量W對未知個體x'進行預測的原理是顯見的：首先將未知個體與特征矩陣X中的個體相乘得到對應的相似度，然後以此相似度乘以alpha的分量，最後在此基礎上以加權求和的方法來計算未知個體x'的目標值。然而，alpha到底是什麼呢？

　　對支持向量機有一定瞭解的同學肯定會有一個基本的認識：支持向量為間隔邊界上的點，相對應的alpha的分量為0。也就是說，最終的權值只會考慮作為支持向量的樣本！然而，進一步，很少有人會去思考：間隔邊界上的點都是支持向量嗎？支持向量所對應的alpha的分量值大小服從什麼規律嗎？支持向量為什麼叫支持向量呢？

　　我們通過一個簡單的例子來進一步解答以上的問題，首先生成特征矩陣X和目標向量y：

 1 import numpy as np
 2 from sklearn.svm import SVC
 3 from matplotlib import pyplot as plt 
 4 
 5 X1_positive_border = np.random.uniform(-10, 10, size=10)
 6 X2_positive_border = X1_positive_border + 1
 7 X_positive_border = np.hstack((X1_positive_border.reshape(-1,1), X2_positive_border.reshape(-1,1)))
 8 
 9 X1_positive = np.random.uniform(-10, 10, size=10)
10 X2_positive = X1_positive + np.random.uniform(2, 10, size=10)
11 X_positive = np.hstack((X1_positive.reshape(-1,1), X2_positive.reshape(-1,1)))
12 
13 X1_negative_border = np.random.uniform(-10, 10, size=10)
14 X2_negative_border = X1_negative_border - 1
15 X_negative_border = np.hstack((X1_negative_border.reshape(-1,1), X2_negative_border.reshape(-1,1)))
16 
17 X1_negative = np.random.uniform(-10, 10, size=10)
18 X2_negative = X1_negative + np.random.uniform(-10, -2, size=10)
19 X_negative = np.hstack((X1_negative.reshape(-1,1), X2_negative.reshape(-1,1)))
20 
21 X = np.vstack((X_positive_border, X_positive, X_negative_border, X_negative))
22 y = np.hstack((np.ones(20), -np.ones(20)))

　　使用線性核的SVC進行訓練：

1 model = SVC(C=0.1, kernel='linear')
2 model.fit(X, y)

　　對訓練的結果繪圖：

 1 #繪製邊界正例
 2 plt.plot(X_positive_border[:,0], X_positive_border[:,1], 'g.', markersize=12, label='Positive X At Border')
 3 #繪製正例
 4 plt.plot(X_positive[:,0], X_positive[:,1], 'g^', markersize=12, label='Positive X')
 5 #繪製邊界反例
 6 plt.plot(X_negative_border[:,0], X_negative_border[:,1], 'r.', markersize=12, label='Negative X At Border')
 7 #繪製反例
 8 plt.plot(X_negative[:,0], X_negative[:,1], 'rv', markersize=12, label='Negative X')
 9 #繪製正邊界
10 plt.plot(np.arange(-10, 11), np.arange(-10, 11) + 1, 'c--')
11 #繪製超平面
12 plt.plot(np.arange(-10, 11), np.arange(-10, 11), 'k-')
13 #繪製負邊界
14 plt.plot(np.arange(-10, 11), np.arange(-10, 11) - 1, 'm--')
15 #繪製座標軸
16 plt.plot(np.arange(-10, 11), np.zeros(21), 'k-')
17 plt.plot(np.zeros(41), np.arange(-20, 21), 'k-')
18 #給每個支持向量進行標註
19 for i in range(len(model.support_vectors_)):
20     x = model.support_vectors_[i]
21     a = model.dual_coef_[0][i] * y[model.support_[i]]
22     plt.annotate('a[%d]=%.2f' % (i, a), xy=(x[0], x[1]), xytext=(x[0]-1, x[1]+1), arrowprops=dict(arrowstyle="->",connectionstyle="arc3"))23 
24 plt.legend(loc='best', shadow=True)
25 plt.show()

　　顯示結果如下：

 　　我們可以看到，當參數C=0.1時，邊界上幾乎所有的點都是支持向量。再設C=1.0時，顯示結果如下：

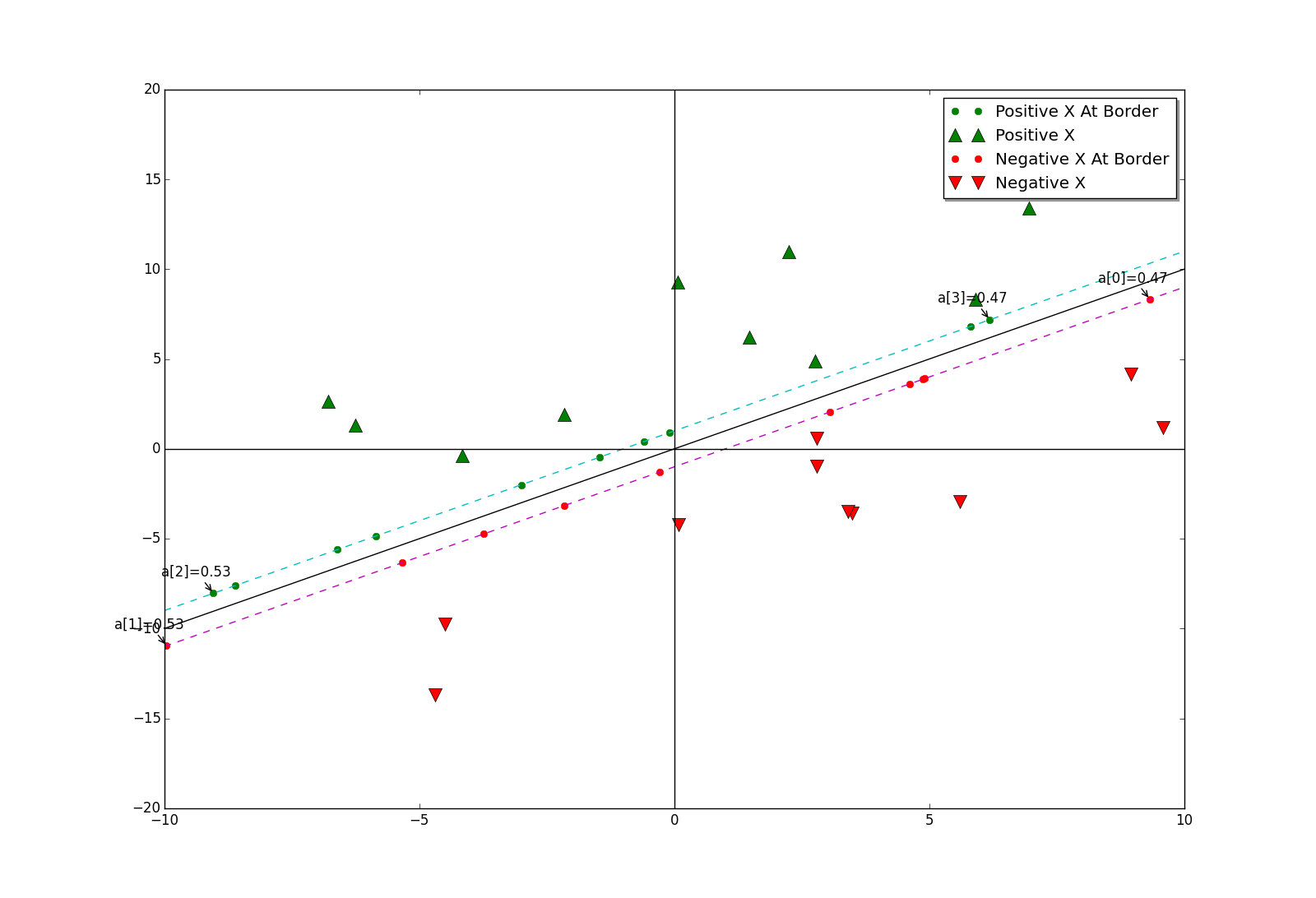
　　此時，只有少數邊界上幾個點是支持向量了。參數C的變化為什麼會影響支持向量的個數呢？官方文檔中對參數C的說明是懲罰繫數，不同於對權值向量的懲罰，這裡的懲罰是針對於alpha的。C越大，懲罰就越大，那麼alpha的非零項就越少。當邊界上只有少數點為支持向量時，通常來說，邊界上靠近兩端的點更適合作為支持向量，例如上圖中的a[0]至a[3]。如何解釋呢？

　　先看負邊界上靠近兩端的點，當它們與目標向量y的分量（值為-1，反向）相乘後，相當於正邊界上的點。正邊界上，對靠近兩端的點進行向量求和，這樣便可方便得到超平面的法向量，即權值向量。通俗一點說，靠近兩端的點都是一些特色的點（不能被其他點代表），其他點可以由這些有特色的點的線性表示。或者更通俗一點來說，靠近兩端的點可以看成是各行各業的先進人士，由於職業不同，他們都不能被彼此代表，但是他們可以代表自己的行業的其他人，他們的組合甚至可以代表一些跨行業的人！

　　此時，我們可以引出結論：支持向量機代表的是一種現實的民主，我國的人民代表大會制也是如此。

　　最後，我們還需要回答一個顯見問題，支持向量的名稱由來：一組能夠”撐起“分隔邊界的向量。

5 總結

　　這次，我們探討了3種常見的線性模型權值向量求解思路。從LMS和隨機梯度下降到最小二乘，再到支持向量機，人們求解自然科學問題的思路與求解社會科學問題的思路走到了一起。最近的一件小事帶給我啟發：居住的小區需要對某一些問題進行決策，一開始由熱心居民每家每戶聽取意見，結果遲遲拿不定主意，越聽越糊塗。到最後，只好選出業主委員會，由業主委員會代表各個特色群體，問題才得以解決。

　　之前對線性模型的權值求解過程和結果都“記得”非常熟悉，但是其真正意義（特別是最小二乘）沒有去深究。而這次能夠受到啟發，並且聯繫到現實生活中，也算是對線性模型有了更進一步的認識吧。

6 參考資料

1. 關於線性模型你可能還不知道的二三事（一、樣本）
2. 支持向量機通俗導論（理解SVM的三層境界）
3. sklearn svc model