一個遞歸函數的分析

自己寫了一個奇奇怪怪的遞歸函數

#include<iostream>
using namespace std;

int i=0,j=0;

void dfs(int u);

void tfs(int u)
{
	if(u>3)
	{
		return;
	}
	j++;	
	cout<<"j="<<j<<" "<<"u="<<u<<endl;//1
	dfs(u+1);//2
	cout<<u<<" "<<"x"<<endl;//3
	tfs(u+2);//4
}

void dfs(int u)
{
	if(u>3)
	{
		return;
	}
	i++;	
	cout<<"i="<<i<<" "<<"u="<<u<<endl;//5
	dfs(u+1);//6
	cout<<u<<" "<<"s"<<endl;//7
	tfs(u+2);//8
}

int main()
{
	dfs(0); 
	return 0;
}

運行結果:

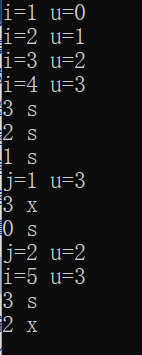
運行過程分析：

開頭dfs(0)，先執行5，輸出i=0 u=0，然後執行6，再執行調用的新的函數5，直到調用到第四個函數時候滿足u>3退出

然後調用的前三個新的函數執行下一步7，越晚調用的函數越早執行下一步

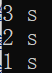
執行8，同樣越晚調用的函數越早執行下一步，只有u=1的時候，tfs(3)滿足!>3不會被return，執行1

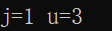
執行2，u=4>3，return，下一步上一步中的函數執行3，併在下一步遞歸4中返回

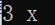
這時候最開始的dfs(0)函數執行7，8，1，2，5，6，7，3

遞歸函數步驟複雜，不容易描述出來具體步驟，大腦在壓棧的時候很難受，不過我們在做題的時候只需要設計好函數，並相信它可以完成任務就可以了。