程式分析與優化 - 11 多分支分析

本章是系列文章的第十一章，主要介紹GPU的編譯原理，分析了多核運行過程中的記憶體分岔和控制流分岔的分析和處理。本文中的所有內容來自學習DCC888的學習筆記或者自己理解的整理，如需轉載請註明出處。周榮華@燧原科技 11.1 什麼是GPU 11.1.1 GPU的發展歷史軟體控制的VGA幀緩衝區頻繁 ...

本章是系列文章的第十一章，主要介紹GPU的編譯原理，分析了多核運行過程中的記憶體分岔和控制流分岔的分析和處理。

本文中的所有內容來自學習DCC888的學習筆記或者自己理解的整理，如需轉載請註明出處。周榮華@燧原科技

11.1 什麼是GPU

11.1.1 GPU的發展歷史

軟體控制的VGA幀緩衝區

頻繁使用的圖形柵格化程式

嘗試用硬體來加速這些處理

流水線化的圖形處理過程，例如變形，映射，切片，顯示等等

工程師開始發現一些過程本身雖然不一樣，但實現該功能的硬體是相似的，例如圖著色

從單獨的圖著色API到泛化的API

GPU指令集的誕生→泛化的整數通用處理函數 → 帶分支支持的處理函數

一個獨立的柵格化處理晶元 + 通用處理晶元

然後柵格化處理晶元又集成到了GPU裡面，變成通用處理晶元的一部分

……

11.1.2 電腦組織

傳統的SIMD（Single Instruction Multiple Data）和SPMD（Single Program Multiple Data）到GPU的MSIMD（Multiple Single-Instruction Multiple-Data）

11.1.3 編程環境

主流編程環境主要有兩種，開源的OpenCL和閉源的C for CUDA，後者是NVIDIA發佈的，前者是其他公司組成的聯盟發佈的。這裡主要說CUDA。

異構編程語言：一個能指定不同異構處理器上執行的編程語言。

傳統的C編程語言做矩陣操作的例子：

1 void saxpy_serial(int n, float alpha, float *x, float *y) {
2   for (int i = 0; i < n; i++)
3     y[i] = alpha * x[i] + y[i];
4 }
5 // Invoke the serial function:
6 saxpy_serial(n, 2.0, x, y);

轉換成CUDA的例子：

1 __global__ void saxpy_parallel(int n, float alpha, float *x, float *y) {
2   int i = blockIdx.x * blockDim.x + threadIdx.x;
3   if (i < n)
4     y[i] = alpha * x[i] + y[i];
5 }
6 // Invoke the parallel kernel:
7 int nblocks = (n + 255) / 256;
8 saxpy_parallel<<<nblocks, 256>>>(n, 2.0, x, y);

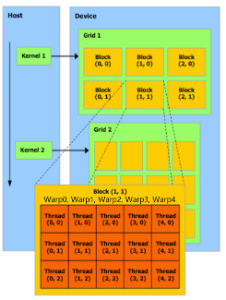
NV的GPU的組織結構：Grids → Blocks → Warps → Threads

Cuda programs = CPU programs + kernels

Kernels調用語法：

kernel<<<dGrd, dBck>>>(A,B,w,C);
指定grids和block

CPU programs → host programs

kernels → PTX (Parallel Thread Execution) → SASS (Streaming ASSembly)

11.2 分岔（Divergence）

英文裡面Divergence有分岔，分支，歧義等多種意思，這裡表示程式執行到某個點之後，可能有多個分支的情況。

11.2.1 SIMD的優缺點

優點：更低的功耗，指令解碼占用空間更少。

對於沒有分支的線性程式，SIMD的性能非常好。但程式幾乎不可避免會存在多個分支。

常見的分支主要有兩類：

因為記憶體訪問地址不一致導致的記憶體分岔
因為控制流分支導致的分岔

11.2.2 控制流分岔的例子

對下麵的cuda 代碼：

1 __global__ void ex(float *v) {
2   if (v[tid] < 0.0) {
3     v[tid] /= 2;
4   } else {
5     v[tid] = 0.0;
6   }
7 }

對應的控制流圖是這樣的：

因為上面程式只有一處分岔（還記得上一章ILP中說的超級塊麽？上面的DAG轉換成樹之後只有2個葉子節點），如果有兩個ALU，我們就可以在無視分岔的情況下把程式執行流水線畫出來：

11.2.3 什麼樣的輸入性能最好？

對下麵的cuda的例子，怎麼樣調整輸入來達到最好的性能？

1 __global__ void dec2zero(int *v, int N) {
2   int xIndex = blockIdx.x * blockDim.x + threadIdx.x;
3   if (xIndex < N) {
4     while (v[xIndex] > 0) {
5       v[xIndex]--;
6     }
7   }
8 }

下麵有五種初始化的方法：

 1 void vecIncInit(int *data, int size) {
 2   for (int i = 0; i < size; ++i) {
 3     data[i] = size - i - 1;
 4   }
 5 }
 6 void vecConsInit(int *data, int size) {
 7   int cons = size / 2;
 8   for (int i = 0; i < size; ++i) {
 9     data[i] = cons;
10   }
11 }
12 void vecAltInit(int *data, int size) {
13   for (int i = 0; i < size; ++i) {
14     if (i % 2) {
15       data[i] = size;
16     }
17   }
18 }
19 void vecRandomInit(int *data, int size) {
20   for (int i = 0; i < size; ++i) {
21     data[i] = random() % size;
22   }
23 }
24 void vecHalfInit(int *data, int size) {
25   for (int i = 0; i < size / 2; ++i) {
26     data[i] = 0;
27   }
28   for (int i = size / 2; i < size; ++i) {
29     data[i] = size;
30   }
31 }

測試下來的結果，在總的執行近似的情況下，沒有分岔和有一個分岔的性能是2倍的差異，正好印證了之前一個分岔需要2個ALU才能確保並行處理的觀點。另外一個分岔的性能和另外觸發了一個隨機數生成器調用的性能接近：

	vecIncInit	vecConsInit	vecAltInit	vecRandomInit	vecHalfInit
總時間	20480000	20480000	20476800	20294984	20480000
實際時間	16250	16153	32193	30210	16157

11.3 分岔的動態檢測

11.3.1 分岔profiling

統計分岔執行時間和執行次數的方法

在並行世界，求程式的profile的過程遠比單核世界複雜，因為需要一個演算法找到那時正在運行的線程將這個profile的結果保存下來。

下麵是常見的找記錄者的演算法：

 1 int writer = 0;
 2 bool gotWriter = false;
 3 while (!gotWriter) {
 4     bool iAmWriter = false;
 5     if (laneid == writer) {
 6       iAmWriter = true;
 7     }
 8   if ( ∃ t ∈ w | iAmWriter == true) {
 9   gotWriter = true;
10   }
11   else {
12     writer++;
13   }
14 }

11.3.2 經典的雙調排序Bitonic Sort

輸入是亂序3/2/4/1，經過5次排序和4次交換之後，變成順序的1/2/3/4

雙調排序的cuda代碼如下：

 1 __global__ static void bitonicSort(int *values) {
 2   extern __shared__ int shared[];
 3   const unsigned int tid = threadIdx.x;
 4   shared[tid] = values[tid];
 5   __syncthreads();
 6   for (unsigned int k = 2; k <= NUM; k *= 2) {
 7     for (unsigned int j = k / 2; j > 0; j /= 2) {
 8       unsigned int ixj = tid ^ j;
 9       if (ixj > tid) {
10         if ((tid & k) == 0) {
11           if (shared[tid] > shared[ixj]) {
12             swap(shared[tid], shared[ixj]);
13           }
14         } else {
15           if (shared[tid] < shared[ixj]) {
16             swap(shared[tid], shared[ixj]);
17           }
18         }
19       }
20       __syncthreads();
21     }
22   }
23   values[tid] = shared[tid];
24 }

我們先不看外面的for迴圈，針對核心的8到20行生成控制流圖：

如果對執行過程做一下trace，大概結果是這樣（上面代碼裡面有4個if，所以轉換成DAG之後就有4個分岔，對應執行時的4個線程）：

第一輪優化，3個分岔變成2個：

 1 unsigned int a, b;
 2 if ((tid & k) == 0) {
 3   b = tid;
 4   a = ixj;
 5 } else {
 6   b = ixj;
 7   a = tid;
 8 }
 9 if (sh[b] > sh[a]) {
10   swap(sh[b], sh[a]);
11 }

優化之後的控制流圖變成這樣（性能提升6.7%）：

第二輪優化，2個分岔變成1個：

1 int p = (tid & k) == 0;
2 unsigned b = p ? tid : ixj;
3 unsigned a = p ? ixj : tid;
4 if (sh[b] > sh[a]) {
5   swap(sh[b], sh[a]);
6 }

實際上?表達式也是完成分岔的功能，但由於大多數指令集都有專門的問號表達式的指令，所以巧妙使用問號表達式將第一重分岔消掉，改進之後的CFG是這樣的（性能提升9.2%）：

11.3.3 總結

性能優化過程主要是消滅分岔，那前面提到的profile數據對這個性能優化有幫助麽？

理論上不論profile數據是什麼樣的，能消滅的分岔肯定優先消滅掉。profile數據對分岔消除的提示是儘可能優先消除執行時間比較長，執行次數比較多的分岔。

拋開分岔問題本身，profile的數據會提示優化執行時間和執行次數比較多的BB。

11.4 分岔的靜態檢測

11.4.1 分岔變數和統一變數

分岔變數（Divergent Variables）：如果一個變數對不同線程會出現不同的值，則稱該變數為分岔變數。

統一變數（Uniform Variables）：如果一個變數在不同線程呈現完全相同的值，則稱該變數為統一變數。

成為分岔變數的幾種場景：

tid是分岔變數
原子操作產生的變數是分岔變數
如果v對分岔變數有數據依賴，則v也是分岔變數
如果v對分岔變數有控制依賴，則v也是分岔變數

分岔變數在數據流圖和控制流圖上具有傳播性。

11.4.2 找到依賴

在一個非SSA的程式裡面，找到某個變數是分岔變數還是非分岔變數是有歧義的，因為一個變數被多次賦值，可能有些賦值生成統一變數，有些賦值生成分岔變數。

但在SSA格式程式中，變數的分岔屬性值就要容易確定的多。

例如下麵的例子中r2在未SSA化之前，可能是分岔變數，也可能是統一變數。右邊SSA化之後，r2_a和r2是分岔變數，r2_b是統一變數。

11.4.3 數據依賴圖DDG

在ILP裡面，我們曾經說過IDG，指令依賴圖，這裡說的數據依賴圖和IDG其實也是類似的，關註的都是數據依賴，不過IDG關註的是指令執行過程的依賴，DDG關註的是數據本身的依賴。

對下麵的CFG，會生成什麼樣的DDG？

對應的DDG如下：

這個數據依賴對ILP可能已經足夠了，但對分岔分析還不夠，有些分岔變數漏掉了！

例如j的值依賴B1裡面的分支，這個分支的條件是個分岔變數，這也會導致j變成分岔變數。所以除了數據依賴外，還需要考慮控制依賴。

11.4.4 控制依賴圖

影響區：一個分支斷言的影響區是該斷言影響的基本塊的集合。

後支配：相對於支配屬性而言，後支配屬性是一個節點B2走到程式結束的每條路徑都要經過B1，則稱為B1後支配B2。

直接後支配：如果節點B1後支配節點B2，並且不存在一個節點B3，B1後支配B3，並且B3後支配B2，則稱為B1是B2的直接後支配。

一個分支斷言的影響區是該分支所在BB到分支的直接後支配BB。

為了方便表示控制依賴導致的後支配，我們將φ函數升級擴展成為帶斷言的φ函數。例如下圖中的x本來只對x0和x1有數據依賴，現在它也對p2有數據依賴：

升級φ函數之後的數據依賴圖：

11.5 分岔優化

11.5.1 同步柵欄刪除

CUDA的ptx指令集預設分支命令都是會產生分岔的，除非特定加上.uni尾碼：

所以在明確肯定不會產生分岔變數的分支命令，可以加上.uni尾碼：

上面的截圖來自PTX ISA :: CUDA Toolkit Documentation (nvidia.com)

11.5.2 寄存器分配

相對於傳統單核的寄存器分配，溢出處理都是直接放到記憶體中，GPU場景下的寄存器溢出可以選擇溢出老本地記憶體和全局記憶體，部分在多個核中共用的變數，還可以考慮放到共用記憶體中。

11.5.3 數據重定位

準排序演算法

將數據切片，每個線程處理一個切片，併在每個切片排序完之後，再拷貝回來：

 1 __global__ static void maxSort1(int *values, int N) {
 2   // 1) COPY-INTO: Copy data from the values vector
 3   // into  shared memory:
 4   __shared__ int shared[THREAD_WORK_SIZE * NUM_THREADS];
 5   for (unsigned k = 0; k < THREAD_WORK_SIZE; k++) {
 6     unsigned loc = k * blockDim.x + threadIdx.x;
 7     if (loc < N) {
 8       shared[loc] = values[loc + blockIdx.x * blockDim.x];
 9     }
10   }
11   __syncthreads();
12   // 2) SORT: each thread sorts its chunk of data
13   // with a  small sorting net.
14   int index1 = threadIdx.x * THREAD_WORK_SIZE;
15   int index2 = threadIdx.x * THREAD_WORK_SIZE + 1;
16   int index3 = threadIdx.x * THREAD_WORK_SIZE + 2;
17   int index4 = threadIdx.x * THREAD_WORK_SIZE + 3;
18   if (index4 < N) {
19     swapIfNecessary(shared, index1, index3);
20     swapIfNecessary(shared, index2, index4);
21     swapIfNecessary(shared, index1, index2);
22     swapIfNecessary(shared, index3, index4);
23     swapIfNecessary(shared, index2, index3);
24   }
25   __syncthreads();
26   // 3) SCATTER: the threads distribute their data
27   // along  the array.
28   __shared__ int scattered[THREAD_WORK_SIZE * 300];
29   unsigned int nextLoc = threadIdx.x;
30   for (unsigned i = 0; i < THREAD_WORK_SIZE; i++) {
31     scattered[nextLoc] = shared[threadIdx.x * THREAD_WORK_SIZE + i];
32     nextLoc += blockDim.x;
33   }
34   __syncthreads();
35   // 4) COPY-BACK: Copy the data back from the shared
36   // memory into the values vector:
37   for (unsigned k = 0; k < THREAD_WORK_SIZE; k++) {
38     unsigned loc = k * blockDim.x + threadIdx.x;
39     if (loc < N) {
40       values[loc + blockIdx.x * blockDim.x] = scattered[loc];
41     }
42   }
43 }

11.6 分岔研究歷史

GPU的歷史都比較新，所以關於GPU的分岔分析資料也比較新：

Ryoo, S. Rodrigues, C. Baghsorkhi, S. Stone, S. Kirk, D. and Hwu, Wen-Mei. "Optimization principles and application performance evaluation of a multithreaded GPU using CUDA", PPoPP, p 73-82 (2008) CUDA介紹
Coutinho, B. Diogo, S. Pereira, F and Meira, W. "Divergence Analysis and Optimizations", PACT, p 320-329 (2011) 分岔分析與優化
Sampaio, D. Martins, R. Collange, S. and Pereira, F. "Divergence Analysis", TOPLAS, 2013. 分岔分析