作為初二的學生,數學題總是令我苦惱的問題。尤其是我們這裡的預備班考試(即我們這裡最好的兩所高中提前一年招生,選拔尖子生的考試)將近,我所面對的數學題越發令人頭疼。 這不,麻煩來了: 如圖,在正方形ABCD中,E在射線BC上,連接AE、CE,則DE/AE的最小值為lxx_____. 拿到這題,信心慢慢 ...
作為初二的學生,數學題總是令我苦惱的問題。尤其是我們這裡的預備班考試(即我們這裡最好的兩所高中提前一年招生,選拔尖子生的考試)將近,我所面對的數學題越發令人頭疼。
這不,麻煩來了:
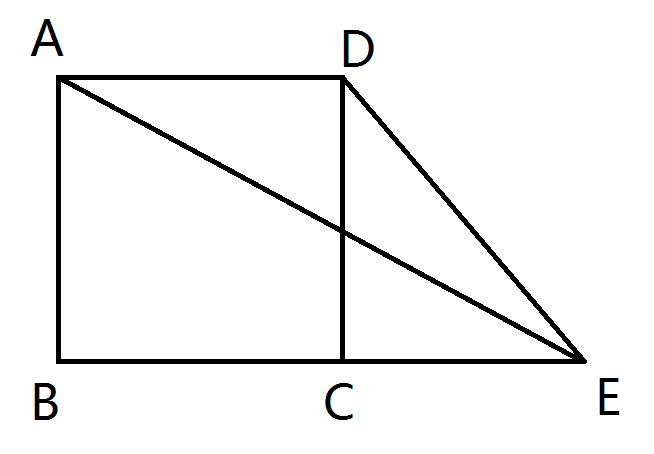
如圖,在正方形ABCD中,E在射線BC上,連接AE、CE,則DE/AE的最小值為________.
拿到這題,信心慢慢的我從容淡定地設AB:CE為1:x,即AB=k,CE=xk,於是原式(設為y)=[k^2+(xk)^2]^0.5/[k^2+(k+xk)^2]^0.5(這裡的“^”代表乘方)。這不就只要求[k^2+(xk)^2]/[k^2+(k+xk)^2]的最小值嘛!這是一個求代數式最小值的問題。
可是……越看越不對勁。這個代數式是個分式,而我們常接觸的同類型題涉及的都只是整式。憑著我對六本初中數學書的印象,我不禁提出疑問:這真的是初中的內容嗎?書上似乎隻字未提吧?
但是,本著埋頭苦幹的老黃牛精神,我就在那裡毫無結果地和這道題目耗了幾個小時。最終,我放棄了。
但也許是夢裡來的靈感,第二天早上,我突然想到:何不通過一個Python程式來逐個列舉,從中選擇近似值呢?
於是,第一個程式出來了:
k=1 answer=100 myx=0 for x in range(10): y=(k**2+(x*k)**2)**0.5/(k**2+(k+x*k)**2)**0.5 if y<answer: answer=y myx=x print(answer,myx)
輸出結果:
0.6324555320336759 1
唉,怎麼越看越不對勁?
最後,我終於發現問題的所在:像這樣遍歷x,它的值都是整數,而事實上最小的y所對應的x不一定是整數。
那好,我們改:
k=1 answer=100 myx=0 for x in range(10000): x=x/1000 y=(k**2+(x*k)**2)**0.5/(k**2+(k+x*k)**2)**0.5 if y<answer: answer=y myx=x print(answer,myx)
輸出:
0.6180339889095493 0.618
這個總沒有問題了吧?還是有問題。你怎麼能確定x的區間?
這個問題看似很致命,但並非完全不可解。我們可以大致推斷,y的變化趨勢應該是先下降後上升或先上升後下降(這個推理對我來說是本能的,以至於我自己都無法詳細解釋過程,但確實可以推理得到這個結論),而既然是求最小值,那自然是前者。因此,由於x從o.618到1是在增加,所以x一定在0.618或其以下,而這些數顯然我們已經遍歷到了(至少在某個精度上)。接下來,我們所需要的只是提高精度,以此來得到更接近真實值的結果,並憑藉它猜測正確答案。
最終,在較高的精度下(程式與前面大致相同,只是加大了遍歷的數值與x縮小的倍數,在此不列出),我們得到結果:
0.6180339887498948 0.618034
我們都知道,黃金分割比的小數點後前65位等於0.6180339887498948482045868343656381177203091798057628621354486227,這個數的前面幾位和我們遍歷的結果完全吻合。我們有理由相信,答案是黃金分割比(5^0.5-1)/2。於是,我們完美地用Python解決了這個問題。
當然,後來我們老師為我們講解了這題不需要程式的解決方法:設法將式子中未知部分化為x+a/x的形式,這個式子永遠不會小於2a^0.5。這樣,我們就可以求得最值了。
代碼的結束,對於程式也許僅僅只是開始;學習的暫時告一段落,從不影響生活的繼續。生命無止境,貴在一顆永遠向上的心。
——“偉大的哲學家”GodForever



