引言 隨機函數演算法應該是電腦史上最重要的十大演算法之一吧. 而C中使用的隨機函數 本文主要圍繞rand 函數找到G點. 就是偽隨機函數的周期值. 關於rand 源碼, 可以從Linux底層源碼 glibc中找. 看了一下大約4個文件. 演算法比較複雜. 感覺很穩定. 這裡不探討隨機演算法的實現. 只為了 ...
引言
隨機函數演算法應該是電腦史上最重要的十大演算法之一吧. 而C中使用的隨機函數
#include <stdlib.h> _Check_return_ _ACRTIMP int __cdecl rand(void);
本文主要圍繞rand 函數找到G點. 就是偽隨機函數的周期值.
關於rand 源碼, 可以從Linux底層源碼 glibc中找. 看了一下大約4個文件. 演算法比較複雜. 感覺很穩定.
這裡不探討隨機演算法的實現. 只為了找到 隨機函數周期.
前言
現在window上測試. 測試代碼 main.c
#include <stdio.h> #include <stdlib.h> #define _INT_R (128) #define _INT_FZ (10000000) // 得到rand() 返回值, 並寫入到文件中 int getrand(long long *pcut) { static int _cut = 0; long long t = *pcut + 1; int r = rand(); // 每次到萬再提醒一下 if(t % _INT_FZ == 0) fprintf(stdout, "%d 個數據跑完了[%d, %lld]\n", _INT_FZ, _cut, t); if(t < 0) { // 數據超標了 ++_cut; fprintf(stderr, "Now %d T > %lld\n", _cut, t - 1); *pcut = 0; // 重新開始一輪 } *pcut = t; return r; } /* * 驗證 rand 函數的周期 */ int main(int argc, char* argv[]) { int rbase[_INT_R]; int i = -1, r; long long cut = 0; // 先產生隨機函數 while(++i < _INT_R) rbase[i] = getrand(&cut); // 這裡開始隨機了 for(;;) { r = getrand(&cut); if (r != rbase[0]) continue; for(i=1; i<_INT_R; ++i) { r = getrand(&cut); if(r != rbase[i]) break; } // 找見了數據 if(i == _INT_R) { printf("Now T = %lld\n", cut); break; } } system("pause"); return 0; }
主要思路是 _INT_R 128個數重疊那我們就認為. 已經找到這個周期了.
測試結果截圖是
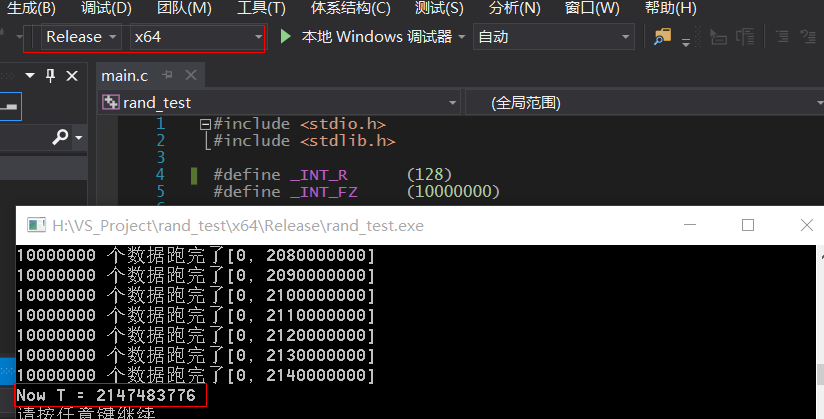
主要採用 Release X64 編譯. 為了檢驗上面結果是可以接受的, 將 _INT_R 改成1024 重新編譯一次.
運行結果如下:
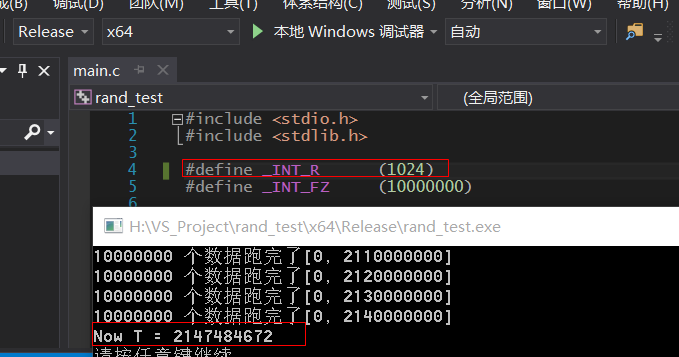
綜合上面我們找見了 window 上 rand 函數的 G點 是
2147483776 - 128 = 214748248
2147484672 - 1024 = 2147483648
因而得到 window 上 VS2015 編譯器的 rand G點 是 2147483648.
G點在游戲中用的很多. 例如抽獎, 掉裝備, 暴擊等等.
正文
1. 在linux 上試試水
在linux上試試 測試代碼基本一樣 rand2.c 如下
#include <stdio.h> #include <stdlib.h> #define _INT_R (1024) #define _INT_FZ (100000000) // 得到rand() 返回值, 並寫入到文件中 int getrand(long long *pcut) { static int _cut = 0; long long t = *pcut + 1; int r = rand(); // 每次到萬再提醒一下 if(t % _INT_FZ == 0) fprintf(stdout, "%d個數據又跑完了[%d, %lld]\n", _INT_FZ, _cut, t); if(t < 0) { // 數據超標了 ++_cut; fprintf(stderr, "Now %d T > %lld\n", _cut, t - 1); *pcut = 0; // 重新開始一輪 } *pcut = t; return r; } /* * 驗證 rand 函數的周期 */ int main(int argc, char* argv[]) { int rbase[_INT_R]; int i = -1, r; long long cut = 0; // 先產生隨機函數 while(++i < _INT_R) rbase[i] = getrand(&cut); // 這裡開始隨機了 for(;;) { r = getrand(&cut); if (r != rbase[0]) continue; for(i=1; i<_INT_R; ++i) { r = getrand(&cut); if(r != rbase[i]) break; } // 找見了數據 if(i == _INT_R) { printf("Now T = %lld\n", cut); break; } } return 0; }
編譯命令
gcc -03 -o randc2.out rand2.c
最後運行結果, 等了 好久還是沒出來.

Linux 上的rand 函數寫的很有水準, 分佈的很隨機. 總而言之這個隨機值比較大. 但一定存在的.
有興趣的可以按照上面思路優化跑一跑. 這邊Ubuntu 是虛擬機跑的慢.
2. 繼續擴展, 減小rand 返回 MAX值 試試水
修改上面 getrand 函數
// _INT_RMAX 表示隨機數範圍 [0, 100) #define _INT_RMAX (100) #define _INT_R (1024) #define _INT_FZ (10000000) // 得到rand() 返回值, 並寫入到文件中 int getrand(long long *pcut) { static int _cut = 0; long long t = *pcut + 1; int r = rand() % _INT_RMAX; // 每次到萬再提醒一下 if (t % _INT_FZ == 0) fprintf(stdout, "%d 個數據跑完了[%d, %lld]\n", _INT_FZ, _cut, t); if (t < 0) { // 數據超標了 ++_cut; fprintf(stderr, "Now %d T > %lld\n", _cut, t - 1); *pcut = 0; // 重新開始一輪 } *pcut = t; return r; }
添加 了 取餘看是否, 影響G點 測試結果
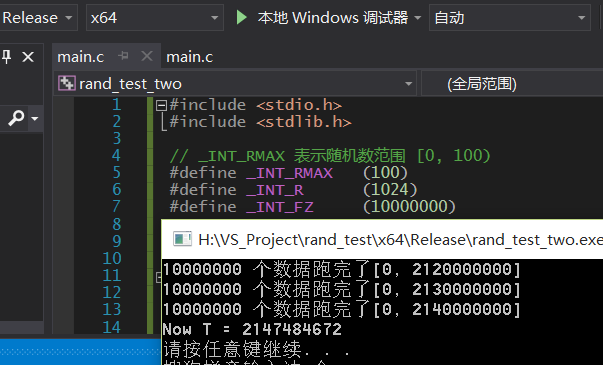
發現G點沒有變化.
可以有推論: rand() 周期不隨著 二次 mod取餘而改變.
因而可以放心 mod使用 偽隨機函數. G點還是那麼大.
3. 最後, 贈送一個常用的 [min, max] 之間的隨機函數
/* * 返回 [min, max] 區間的隨機函數 * min : 起始位置 * max : 結束位置 * : 返回[min, max]區間之內的位置 */ extern int random(int min, int max); /* * 返回 [min, max] 區間的隨機函數 * min : 起始位置 * max : 結束位置 * : 返回[min, max]區間之內的位置 */ int random(int min, int max) { assert(min < max); // 正常情況 return rand() % (max - min + 1) + min; }
測試demo 代碼 結構如下
#include <stdio.h> #include <stdlib.h> #include <time.h> #include <assert.h> /* * 返回 [min, max] 區間的隨機函數 * min : 起始位置 * max : 結束位置 * : 返回[min, max]區間之內的位置 */ extern int random(int min, int max); /* * C 基礎, 使用隨機函數 */ int main(int argc, char* argv[]) { int min = -5, max = 5; int i = 0; // 開始統一 初始化種子 srand((unsigned)time(NULL)); while(i < 100) { printf("%3d ", random(min, max)); if (++i % 10 == 0) putchar('\n'); } system("pause"); return 0; } /* * 返回 [min, max] 區間的隨機函數 * min : 起始位置 * max : 結束位置 * : 返回[min, max]區間之內的位置 */ int random(int min, int max) { assert(min < max); // 正常情況 return rand() % (max - min + 1) + min; }
測試結果是

基本比較穩定. 一切都在預料之中.
總結 本文 得出兩個 推論
a. rand()偽隨機函數, 存在G點. 並且可以找到
b. G點 不隨著 二次 mod 取餘改變.
後記
錯誤是難免的, 預祝明天愉快~~



