1 問題的提出 對於給定的數據集 \(D = \{(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)\}\),線性回歸 (linear regression) 試圖學得一個線性模型以儘可能準確地預測是指輸出標記. 2 原理 設給定的數據集 \(D = \{(x_i,y_i)\} ...
目錄
1 問題的提出
對於給定的數據集 \(D = \{(x_1,y_1),(x_2,y_2),\cdots,(x_m,y_m)\}\),線性回歸 (linear regression) 試圖學得一個線性模型以儘可能準確地預測是指輸出標記.
2 原理
設給定的數據集 \(D = \{(x_i,y_i)\}_{i=1}^m, \ x_i,y_i \in \mathcal{R}\). 對於離散屬性,如果屬性值間存在“序”(order)的關係,可通過連續化將其轉化為連續值,例如二值屬性“身高”的取值“高”“矮”可轉化為 \(\{1.0,0.0\}\),三值屬性“高度”的取值“高”“中”“低”可轉化為 \(\{1.0,0.5,0.0\}\);若屬性之間不存在有序關係,假定有 \(k\) 個屬性值,則通常轉化為 \(k\) 維向量,例如屬性“瓜類”的取值“西瓜”“南瓜”“黃瓜”可轉化為 \((0,0,1),(0,1,0),(1,0,0)\).
線性回歸試圖學得
\[f(x_i) = wx_i + b, \ s.t. f(x_i) \simeq y_i \tag{1} \]2.1 代價函數
我們需要確定 \(w\) 和 \(b\) 的值使得 \(f(x)\) 和 \(y\) 之間的差別儘可能小. 因此我們引入均方誤差,均方誤差是回歸問題中最常用的性能度量工具,我們可以試圖讓均方誤差最小化,即
\[\begin{aligned} (w^*,b^*) &= \arg\min\limits_{(w,b)} \sum_{i=1}^m(f(x_i)-y_i)^2\\ &=\arg\min\limits_{(w,b)} \sum_{i=1}^m(y_i-wx_i-b)^2 \end{aligned} \tag{2} \]\(\arg\min\limits_{\theta}f(x;\theta)\) 意思就是找出一個 \(\theta\) 使得 \(f(x;\theta)\) 的值最小,即他的返回值是 \(f(x;\theta)\) 的最小值所對應的 \(\theta\) 的值.
均方誤差有很好的幾何意義,它對應了常用的“歐式距離”(Euclidean distance),基於均方誤差最小化的進行模型求解的方法稱為“最小二乘法”(least square method). 線上性回歸中,最小二乘法就是試圖尋找一條直線,使得所有樣本點到直線的歐氏距離之和最小.
在均方誤差的基礎上進一步構造代價函數
\[J(w,b) = \frac{1}{2m}\sum_{i=1}^m(f(x_i)-y_i)^2 = \frac{1}{2m}\sum_{i=1}^m(wx_i + b - y_i)^2 \]這裡分母的 \(2\) 是為了後續求導的方便
求解 \(w\) 和 \(b\) 使 \(J(w,b)\) 最小化的過程,稱為線性回歸模型的最小二乘“參數估計”(parameter estimation). 我們可將 \(J(w,b)\) 分別對 \(w\) 和 \(b\) 求導,得到
\[\begin{aligned} &\frac{\partial J(w,b)}{\partial w} = \frac{1}{m}\sum_{i=1}^m(wx_i+b-y_i)x_i\\ &\frac{\partial J(w,b)}{\partial b} = \frac{1}{m}\sum_{i=1}^m(wx_i+b-y_i) \end{aligned} \]令上兩式等於0,解得
\[w = \frac{\sum_{i=1}^my_i(x_i-\bar{x})}{\sum_{i=1}^mx_i^2-\frac{1}{m}(\sum_{i=1}^mx_i)^2}\\ b = \frac{1}{m}\sum_{i=1}^m(y_i-wx_i) \]\(J(w,b)\) 是關於 \(w,b\) 的凸函數,根據凸函數的性質,其偏導為 \(0\) 時就是 \(w\) 和 \(b\) 的最優解.
其中 \(\bar{x} = \frac{1}{m}\sum_\limits{i=1}^mx_i\) 為 \(x\) 的均值.
2.2 模型的評價
2.2.1 皮爾遜相關係數
使用相關係數衡量線性相關性的強弱,皮爾遜相關係數的公式如下:
\[r_{xy} = \frac{COV(X,Y)}{\sqrt{Var(X)Var(Y)}} \]相關度越高,皮爾遜相關係數的值就趨於 1 或 -1 (趨於 1 表示它們呈正相關, 趨於 -1 表示它們呈負相關);如果相關係數等於0,表明它們之間不存線上性相關關係.
2.2.2 決定繫數
決定繫數 \(R^2\) 也稱擬合優度,反應了 \(y\) 的波動有多少百分比能被 \(x\) 的波動所描述. 決定繫數越接近 1 ,說明擬合程度越好.
總平方和
\[SST = \sum_{i=1}^n(y_i-\bar{y})^2 \]回歸平方和
\[SSR = \sum_{i=1}^n(\hat{y}_i-\bar{y})^2 \]殘差平方和
\[SSE = \sum_{i=1}^n(y_i-\hat{y}_i)^2 \]其中
\[SST = SSR + SSE\\ R^2 = \frac{SSR}{SST} = 1- \frac{SSE}{SST} \]3 Python 實現
3.1 不調sklearn庫
Step1. 調庫
import numpy as np
from numpy import genfromtxt
import matplotlib.pyplot as plt
Step2. 數據導入並繪製散點圖
data = genfromtxt("data.csv", delimiter = ",")
x = data[:, 0, np.newaxis]
y = data[:, 1, np.newaxis]
plt.scatter(x, y)
plt.show()
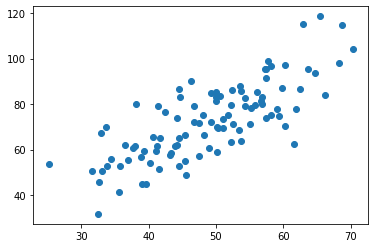
Step3. 求回歸繫數
根據先前的推導,已經知道
m = len(x)
x_bar = np.mean(x)
w = (np.sum((x - x_bar)*y))/(np.sum(x**2)-(1/m)*(np.sum(x))**2)
b = np.mean(y-w*x)
print(w,b)
1.3224310227553517 7.991020982270779
Step4. 擬合圖像
plt.plot(x, y, 'b.')
plt.plot(x, w*x+b, 'r')
plt.show()

Step5. 計算相關係數和決定繫數
COVxy = np.cov(x.T,y.T)
r = COVxy[0,1]/(x.std()*y.std())
print(r)
0.78154393928063
y_hat = w*x+b
SSR = np.sum((y_hat-np.mean(y))**2)
SST = np.sum((y-np.mean(y))**2)
R2 = SSR/SST
print(R2)
0.5986557915386548
3.2 調 sklearn 庫
建模:
from sklearn.linear_model import LinearRegression
model = LinearRegression()
model.fit(x, y)
LinearRegression()
擬合圖像的得出
plt.plot(x, y, 'b.')
plt.plot(x, model.predict(x), 'r')
plt.show()

回歸繫數
w = model.intercept_
b = model.coef_
print("截距為 {0}, 回歸繫數為 {1}".format(w[0], b[0][0]))
截距為 7.991020982270385, 回歸繫數為 1.32243102275536
決定繫數
model.score(x, y)
0.598655791538662
4 梯度下降法
4.1 原理
由於代價函數是凸函數,因此只有全局最小值,梯度下降法的原理是先定一個初始值,然後利用導數就像階梯一樣慢慢逼近全局最小值

已知代價函數 \(J(w,b)\),我們需要找一組 \(w,b\) 使得 \(J(w,b)\) 最小,給定一個演算法:
\[\begin{aligned} &給定 \ w,b \ 的初始值 \ w_0,b_0\\ \\ &repeat until convergence \ \{\\ &\quad\quad temp0 = w - \alpha \frac{\partial}{\partial w}J(w,b)\\ &\quad\quad temp1 = b - \alpha \frac{\partial}{\partial b}J(w,b)\\ &\quad\quad w = temp0\\ &\} \end{aligned} \]其中 \(\alpha\) 為學習率,學習率不能太大也不能太小,可以多次嘗試 \(0.1,0.03,0.01,0.003,0.001,0.0003,\cdots\).
根據已知條件,有
\[J(w,b) = \frac{1}{2m}\sum_{i=1}^m(wx_i + b - y_i)^2\\ \frac{\partial J(w,b)}{\partial w} = \frac{1}{m}\sum_{i=1}^m(wx_i+b-y_i)x_i\\ \frac{\partial J(w,b)}{\partial b} = \frac{1}{m}\sum_{i=1}^m(wx_i+b-y_i) \]於是
\[w = w - \alpha \frac{1}{m}\sum_{i=1}^m(wx_i+b-y_i)\\ b = b - \alpha \frac{1}{m}\sum_{i=1}^m(wx_i+b-y_i)x_i \]4.2 Python實現
# 學習率learning rate
lr = 0.0001
# 截距初值
b = 0
# 斜率初值
w = 0
# 最大迭代次數
epochs = 50
# 最小二乘法
def compute_error(b, w, x, y):
totalError = 0
for i in range(0, len(x)):
totalError += (y[i] - (w * x[i] + b)) ** 2
return totalError / float(len(x)) / 2.0
def gradient_descent_runner(x, y, b, w, lr, epochs):
# 計算總數據量
m = float(len(x))
# 迴圈epochs次
for i in range(epochs):
b_grad = 0
w_grad = 0
# 計算梯度的總和再求平均
for j in range(0, len(x)):
b_grad += -(1/m) * (y[j] - ((w * x[j]) + b))
w_grad += -(1/m) * x[j] * (y[j] - ((w * x[j]) + b))
# 更新 b 和 w
b = b - (lr * b_grad)
w = w - (lr * w_grad)
# 每迭代5次,輸出一次圖像
if i % 5 == 0:
print('epochs:', i)
plt.plot(x, y, 'b.')
plt.plot(x, w*x + b, 'r')
plt.show()
return b,w
print('Starting b = {0}, w = {1}, error = {2}'.format(b, w, compute_error(b, w, x, y)))
print('Running')
b, w = gradient_descent_runner(x, y, b, w, lr, epochs)
print('After {0} iterations b = {1}, w = {2}, error = {3}'.format(epochs, b, w, compute_error(b,w,x,y)))
# 畫圖
plt.plot(x, y, 'b.')
plt.plot(x, w * x + b, 'r')
plt.show()
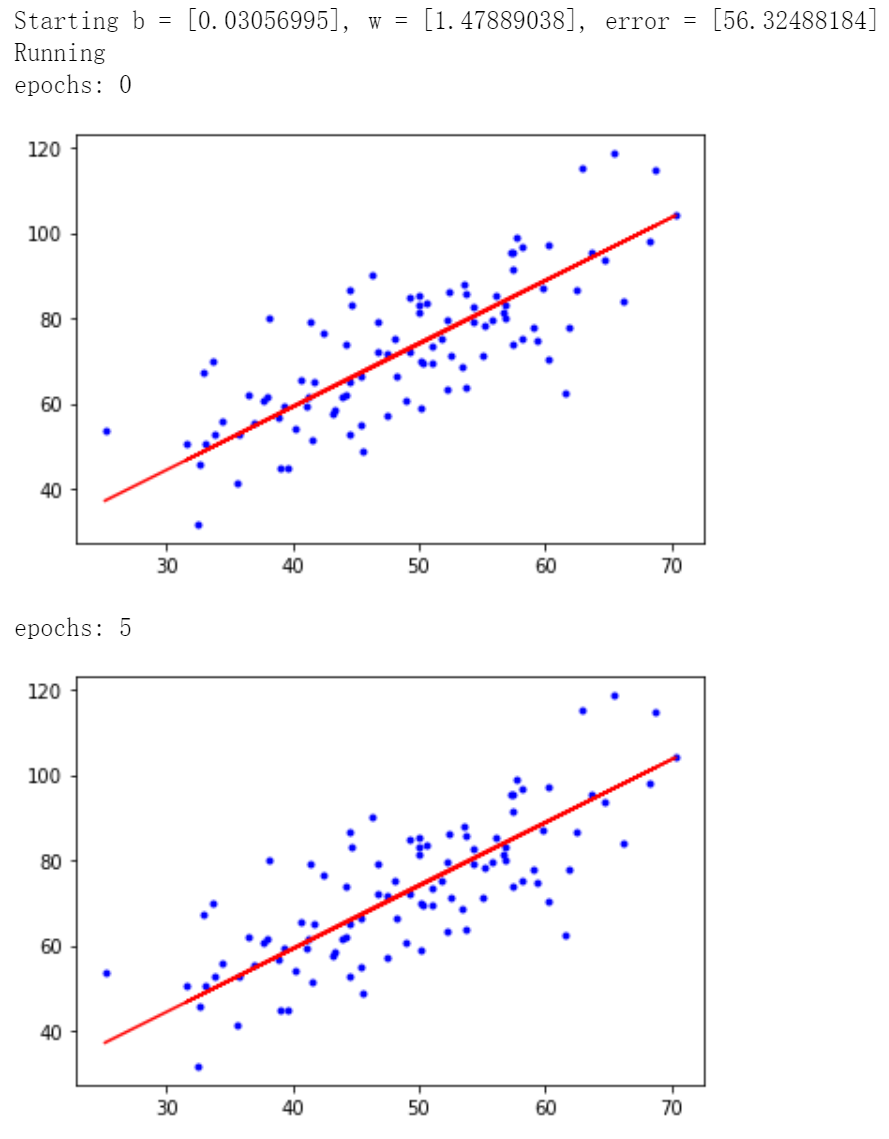

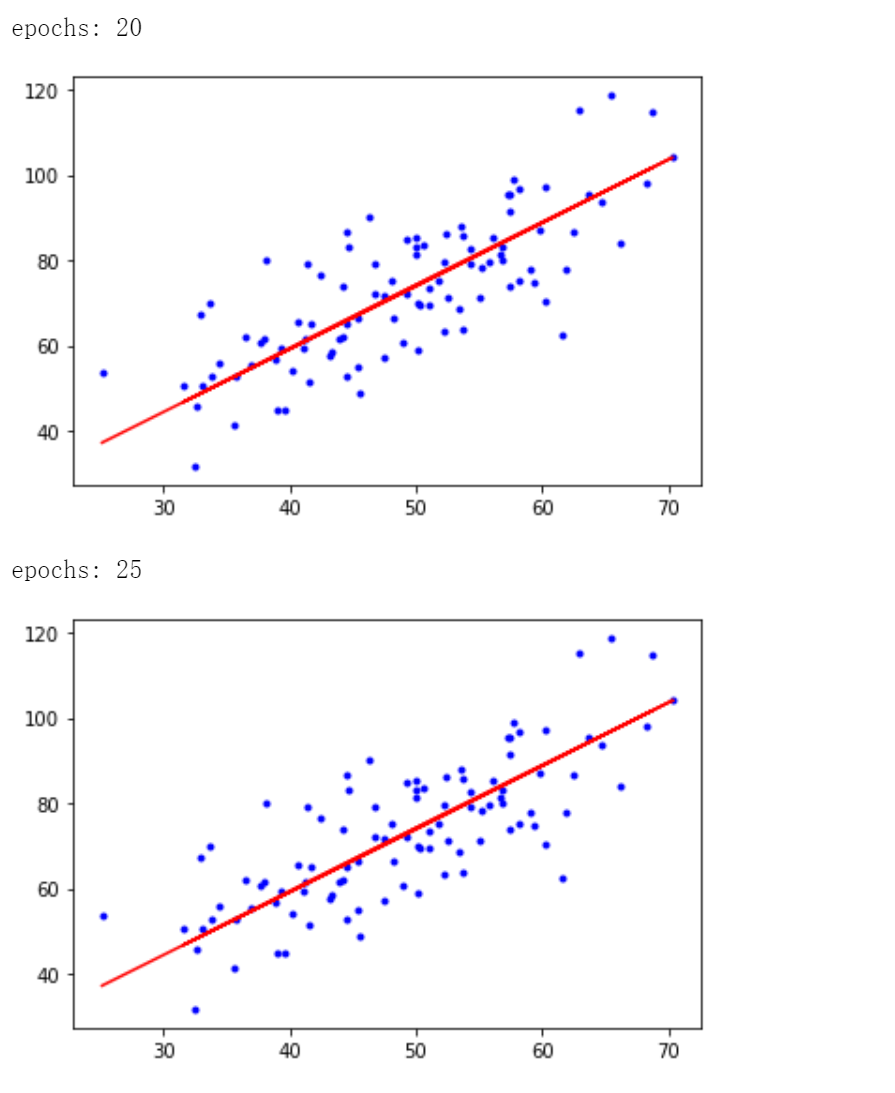
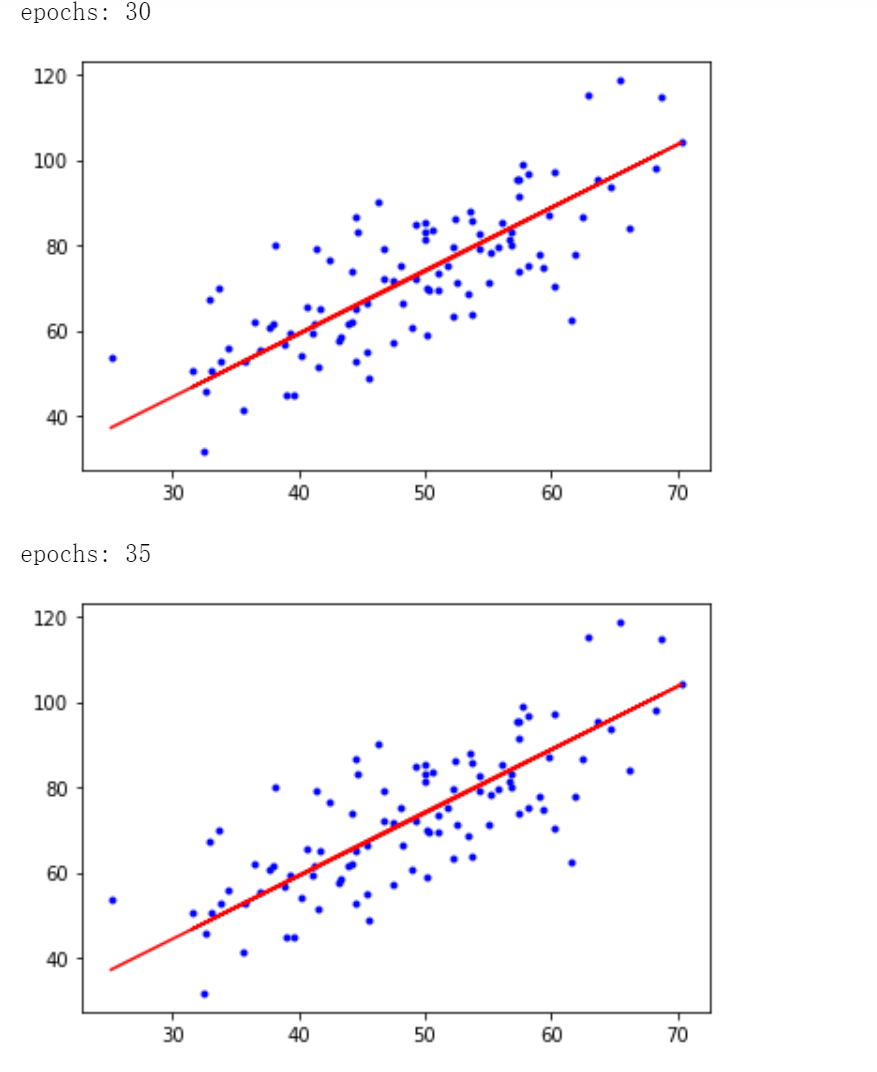
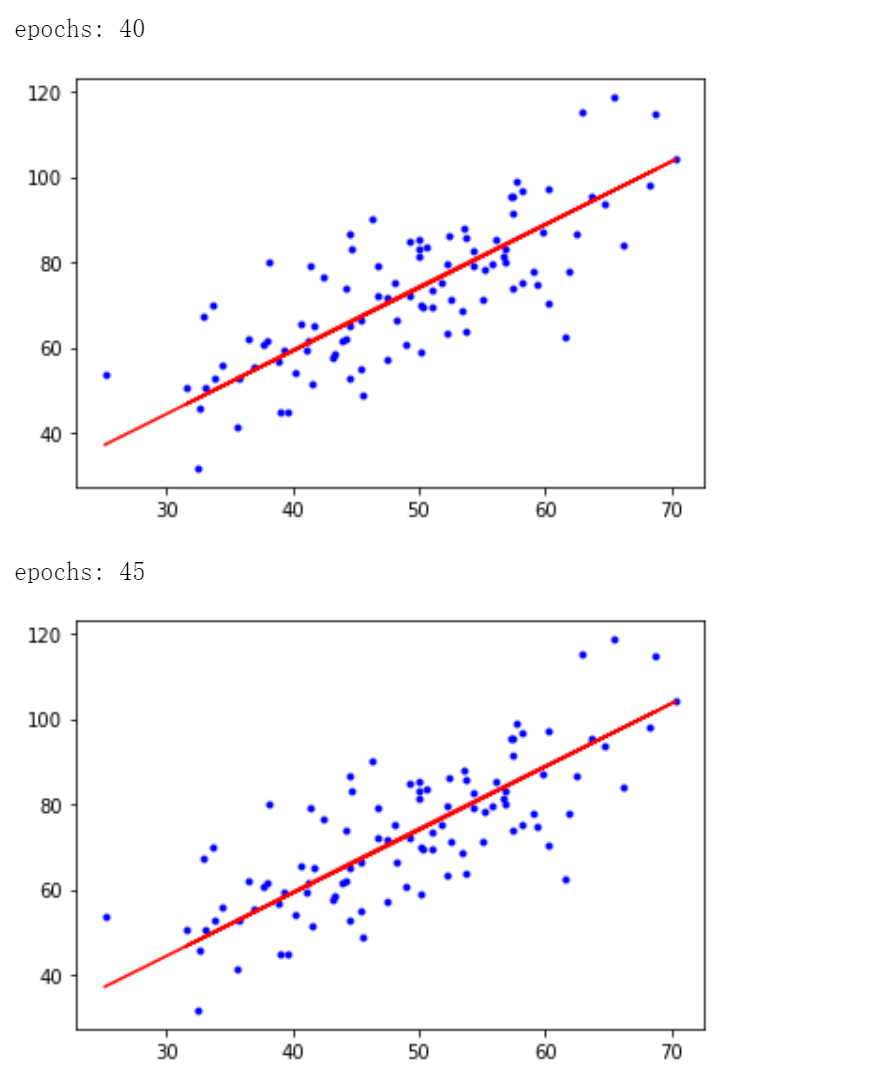
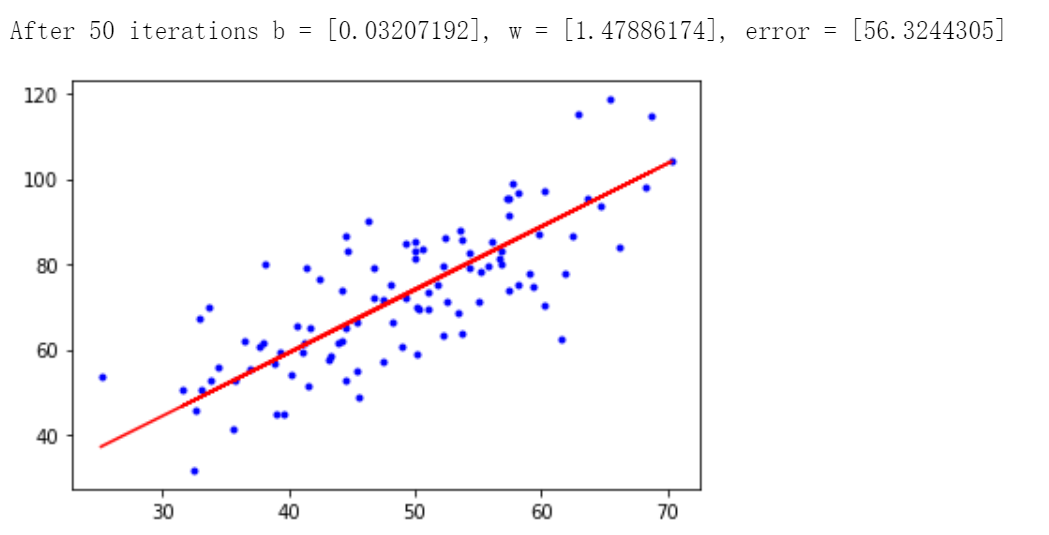
迭代50次後得到 \(b = 0.03207192, w = 1.47886174\),最小二乘誤差為 56.3244305.
參考
[1]. 周志華.《機器學習》.清華大學出版社
[2]. https://www.bilibili.com/video/BV1Rt411q7WJ?p=4&vd_source=08d2535b05740d396ec0fc720c52f36a


