面向對象設計與構造2022第三單元總結

来源:https://www.cnblogs.com/LaiAng80686/archive/2022/06/04/16334952.html
-Advertisement-
Play Games

哈工大軟體構造Lab2中Assert的使用總結，可供後來學子借鑒學習 ...


一、分析在本單元自測過程中如何利用JML規格來準備測試數據

我在本單元的自測中主要採取了兩種測試方法：普遍測試和專項測試。

所謂普遍測試就是數據生成器生成的數據包含作業指導書給出的所有指令，進行覆蓋檢查，但是每種指令的測試不一定是邊界、極端情形。

而專項測試就是基於JML規格，針對那些過程複雜、容易寫錯和出現性能問題的指令生成特殊數據來測試。接下來舉幾個例子來說明。

首先是qgvs指令，從圖論的角度來說其實就是維護一個群組裡面人員所有邊權和的兩倍。我們來看JML是如何描述的

//in Network.java
/*@ public normal_behavior
      @ requires (\exists int i; 0 <= i && i < groups.length; groups[i].getId() == id);
      @ ensures \result == getGroup(id).getValueSum();
      @ also
      @ public exceptional_behavior
      @ signals (GroupIdNotFoundException e) !(\exists int i; 0 <= i && i < groups.length;
      @          groups[i].getId() == id);
      @*/
public /*@ pure @*/ int queryGroupValueSum(int id) throws GroupIdNotFoundException;

//in Group.java
/*@ ensures \result == (\sum int i; 0 <= i && i < people.length; 
      @          (\sum int j; 0 <= j && j < people.length && 
      @           people[i].isLinked(people[j]); people[i].queryValue(people[j])));
      @*/
public /*@ pure @*/ int getValueSum();

所以直接從JML看，複雜度是\(O(指令數*組內人數^2)\)的

但其實從構造數據的角度我還需要關註的是

/*@ public normal_behavior
	  @ ...(省略)
      @ also
      @ public normal_behavior
      @ requires (\exists int i; 0 <= i && i < groups.length; groups[i].getId() == id2) &&
      @           (\exists int i; 0 <= i && i < people.length; people[i].getId() == id1) &&
      @            getGroup(id2).hasPerson(getPerson(id1)) == false && 
      @             getGroup(id2).people.length >= 1111;
      @ assignable \nothing;
      @ also
      @ public exceptional_behavior
      @ ...(省略)
      @*/
    public void addToGroup(int id1, int id2) throws GroupIdNotFoundException,
            PersonIdNotFoundException, EqualPersonIdException;

其實這個方法的JML就約束好了每個群組的人數不得超過1111個人。

因此可以構造人數達到上限的數據來檢驗時間複雜度是否合法，該部分的構造代碼如下

#include <bits/stdc++.h>
using namespace std;
mt19937 rng(time(0));
int main()
{
    freopen("testcase1.txt","w",stdout);
    for(int i=1;i<=1111;i++)
    {
        printf("ap %d AAJ %d\n",i,rng()%200);
    }
    printf("ag 114514\n");
    for(int i=1;i<=1111;i++)
    {
        printf("atg %d 114514\n",i);
    }
    for(int i=1;i<=2777;i++)
        printf("qgvs 114514\n");
    return 0;
}

然後，是qlc指令，我們來看一下它的JML。

    /*@ public normal_behavior
      @ requires contains(id);
      @ ensures \result ==
      @         (\min Person[] subgroup; subgroup.length % 2 == 0 &&
      @           (\forall int i; 0 <= i && i < subgroup.length / 2; subgroup[i * 2].isLinked(subgroup[i * 2 + 1])) &&
      @           (\forall int i; 0 <= i && i < people.length; isCircle(id, people[i].getId()) <==>
      @             (\exists int j; 0 <= j && j < subgroup.length; subgroup[j].equals(people[i]))) &&
      @           (\forall int i; 0 <= i && i < people.length; isCircle(id, people[i].getId()) <==>
      @             (\exists Person[] connection;
      @               (\forall int j; 0 <= j && j < connection.length - 1;
      @                 (\exists int k; 0 <= k && k < subgroup.length / 2; subgroup[k * 2].equals(connection[j]) &&
      @                   subgroup[k * 2 + 1].equals(connection[j + 1])));
      @                connection[0].equals(getPerson(id)) && connection[connection.length - 1].equals(people[i])));
      @           (\sum int i; 0 <= i && i < subgroup.length / 2; subgroup[i * 2].queryValue(subgroup[i * 2 + 1])));
      @ also
      @ public exceptional_behavior
      @ signals (PersonIdNotFoundException e) !contains(id);
      @*/
    public /*@ pure @*/ int queryLeastConnection(int id) throws PersonIdNotFoundException;

正如老師在總結課上所言，其實這種最優化的描述是不太直觀的，不過在閱讀qlc的JML之前我們已經在測驗環節中讀過一個求邊集的JML，所以有了經驗。這裡說白了就是要求id這個人所在連通塊的最小生成樹大小。

從構造數據角度，要檢驗最小生成樹求解的效率和正確性，就是儘可能得讓這個連通塊的邊數要多，而且權值要隨機多樣。構造代碼如下

for(int i=1;i<=1111;i++)
{
     printf("ap %d AAJ %d\n",i,rng()%200);
}
printf("ag 114514\n");
for(int i=1;i<=1111;i++)
{
	printf("atg %d 114514\n",i);
}
for(int i=1;i<=1110;i++)
	printf("ar %d %d %d\n",i,i+1,rng()%1000);
for(int i=1;i<=1109;i++)
	printf("ar %d %d %d\n",i,i+2,rng()%1000);
for(int i=1;i<=538;i++)
	printf("ar %d %d %d\n",rng()%1111+1,rng()%1111+1,rng()%1000);
for(int i=1;i<=20;i++)
	printf("qlc %d\n",rng()%1111+1);

第三，是sim指令，JML太長就略去了。說白了就是除了發送信息外要求出從發送者到接收者的最短路。考慮到朴素的Dijkstra的複雜度是\(O(n^2)\)，而堆優化的Dijkstra複雜度為\(O(m \log n)\)，所以從構造數據角度，人數要達到\(10^3\)量級，同時信息數量與\(sim\)指令數一致達到上限，再加上邊權隨機性，就可以檢測實現的正確性和效率了。

for i in range(0, 1111):
    print("ap %d Jack%d %d" % (i, i, 20), file=file_out)
for i in range(0, 2889):
    print(
        "ar %d %d %d"
        % (random.randint(0, 1111), random.randint(0, 1111), random.randint(0, 1000)),
        file=file_out,
    )
for i in range(0, 500):
    print(
        "am %d %d 0 %d %d"
        % (
            i,
            random.randint(-1000, 1000),
            random.randint(0, 1111),
            random.randint(0, 1111),
        ),
        file=file_out,
    )
for i in range(0, 500):
    print("sim %d" % (i), file=file_out)

第四，是dce指令。如果說前面的三種指令可能構造更多著眼於性能考慮，那麼dce指令的測試就旨在檢查正確性。

通過閱讀JML，其實這條指令需要做兩件事

  • 將已經保存的表情中，熱度小於\(limit\)的刪掉

    @ ensures (\forall int i; 0 <= i && i < \old(emojiIdList.length);
      @          (\old(emojiHeatList[i] >= limit) ==>
      @          (\exists int j; 0 <= j && j < emojiIdList.length; emojiIdList[j] == \old(emojiIdList[i]))));

  • 把所有信息裡面，只保留非表情信息，和所含表情沒有在第一步刪掉的表情信息

     @ ensures (\forall int i; 0 <= i && i < \old(messages.length);
      @          (\old(messages[i]) instanceof EmojiMessage &&
      @           containsEmojiId(\old(((EmojiMessage)messages[i]).getEmojiId()))  ==>
      @           (\exists int j; 0 <= j && j < messages.length; messages[j].equals(\old(messages[i])))));

所以從構造數據來說，一方面人數要少，但是信息量要大，這樣才能讓每種表情的熱度儘量高，另一方面可以讓\(limit\)遞減來進行dce.故構造代碼如下

for i in range(0, 10):
    print("ap %d Jack%d %d" % (i, i, 20), file=file_out)
for i in range(0, 10):
    for j in range(1, 10 - i):
        print("ar %d %d %d" % (i, i + j, random.randint(0, 1000)), file=file_out )
for i in range(0, 20):
    print(
        "sei %d" % (i),
        file=file_out,
    )
for i in range(0, 1000):
    print(
        "aem %d %d 0 %d %d"
        % (i, random.randint(0, 19), random.randint(0, 9), random.randint(0, 9)),
        file=file_out,
    )
for i in range(0, 1000):
    print("sm %d" % (i), file=file_out)
for i in range(0, 50):
    print("dce %d" % (i), file=file_out)
    for j in range(0, 20):
        print("qp %d" % (j), file=file_out)

第五，是群發紅包問題。這個地方我也差點寫錯了。關鍵處的JML就是這一句

@ ensures (\old(getMessage(id)) instanceof RedEnvelopeMessage) ==>
      @          (\exists int i; i == ((RedEnvelopeMessage)\old(getMessage(id))).getMoney()/\old(getMessage(id)).getGroup().getSize();
      @           \old(getMessage(id)).getPerson1().getMoney() ==
      @           \old(getMessage(id).getPerson1().getMoney()) - i*(\old(getMessage(id)).getGroup().getSize() - 1) &&
      @           (\forall Person p; \old(getMessage(id)).getGroup().hasPerson(p) && p != \old(getMessage(id)).getPerson1();
      @           p.getMoney() == \old(p.getMoney()) + i));
  1. 發送的總錢數按照群組總人數均分，但是這個除法和Java運算符一致——是整除。所以會出現\(getMoney()\not=i*getSize()\)的情況
  2. 發送者扣錢但不扣“自己的那一份”，同樣的，發錢也不發“自己的那一份”

但是在具體實現上，我是把這個\(i\)傳到群組裡，在群組裡實現了一個方法，就是給所有人發錢\(i\)元。這就導致這條信息的發送者多得了一份錢。

這個問題是我在截止日那天上午才發現的，之所以大量的普遍測試沒有觸發這個bug，原因就是紅包的錢數最多200，而普遍測試中往往給一個組塞了一千多號人，結果按照整除規則，其他人一分錢沒得，發送者也根本沒有發出去錢。

因此在專項測試中，人數一定要少，而且每發送一條消息，必須要檢查發送者的錢數，再隨機抽查兩個人的錢數，這樣就能較為充分地檢查行為的正確性了。構造代碼如下

for i in range(0, 10):
    print("ap %d Jack%d %d" % (i, i, 20), file=file_out)
print("ag 114514", file=file_out)
for i in range(0, 10):
    print("atg %d 114514" % (i), file=file_out)
send_people = []
for i in range(0,990):
    sender = random.randint(0, 9)
    send_people.append(sender)
    print(
        "arem %d %d 1 %d 114514" % (i, random.randint(0, 200), sender),
        file=file_out,
    )
for i in range(0, 990):
    print("sm %d" % (i), file=file_out)
    print("qm %d" % (send_people[i]), file=file_out)
    for j in range(0, 2):
        print("qm %d" % (random.randint(0, 9)), file=file_out)

二、梳理本單元的架構設計，分析自己的圖模型構建和維護策略

首先還是放一張第三次作業時的UML圖

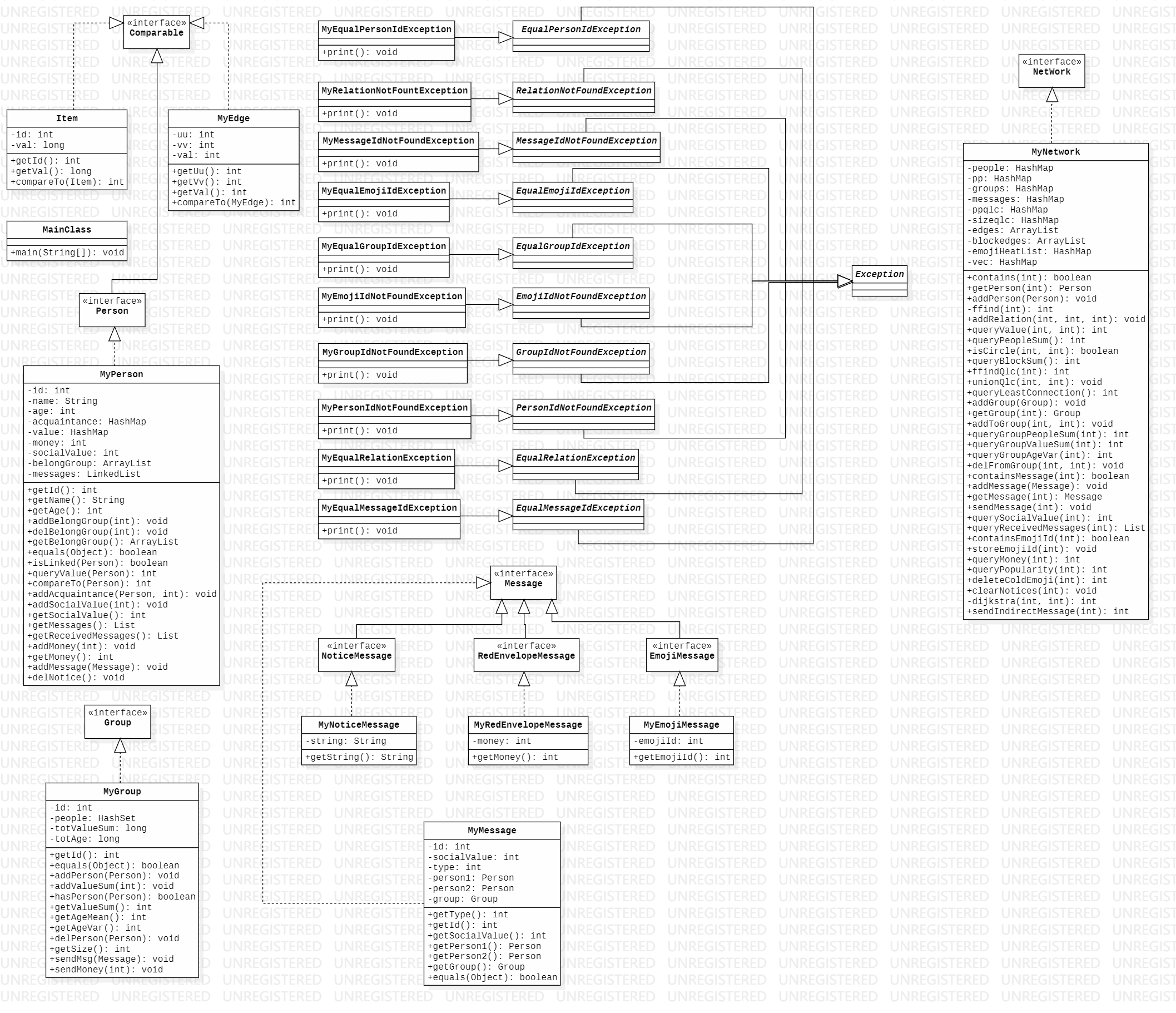
​ 由圖片可知，其實主體框架根據JML基本上已經確定了。自主實現的部分主要是圖模型和一些輔助的方法上。

​ 首先來說圖模型，在求qci和qlc指令時維護了並查集，體現在UML圖上就是MyNetwork裡面的pp、ppqlc和sizeqlc三個HashMap，和ffind、ffindQlc和unionQlc三個方法。其中pp和ffind主要是用並查集維護圖的連通性，便於qci指令中回答兩個人是否連通。而ppqlc、sizeqlc和剩下兩個方法，其實是在用Kruskal演算法求最小生成樹中維護並查集的。為了避免混淆，所以單獨又實現了一下。當然，用於qci的並查集簡單採用路徑壓縮，而在Kruskal演算法中的並查集是路徑壓縮+按秩合併的，以儘可能提高效率。

​ 為了方便Kruskal演算法，新建了一個MyEdge類，可以存儲一條邊的兩個節點和邊權，並實現了Comparable介面，使得其可以排序.

​ 那麼到了sim指令需要寫堆優化的Dijkstra演算法時，需要維護一個無向圖，鄰接表的出現就很有必要了。於是在MyNetwork中有了一個private HashMap<Integer, HashMap<Integer, Integer>> vec;來存起點、終點和這條邊的權值（本單元根據JML規格不會出現重邊，所以這麼維護倒也無妨）。那麼在實現Dijkstra中，使用優先隊列PriorityQueue來選取當前起點所到達的各個點中路徑長度最小的一個點，這裡也新建了一個Item類來方便PriorityQueue的操作。

​ 還有一處圖模型，就是qgvs需要知道一個群組裡所有連邊的權值和*2.不過這裡僅僅需要一個數值，並不需要實際維護裡面的圖結構。需要註意的就是在人員剛剛加入群組的時候，對群組權值和貢獻，人員退出的時候，減去貢獻。特殊的情形就是兩個人可能之前已經屬於一個（或多個）群組，但還沒有建立關係，這個時候addRelation需要考慮到對所有共同加入的群組進行貢獻。

三、按照作業分析代碼實現出現的性能問題和修複情況

​ 由於在設計階段充分考慮了各種指令的最壞時間複雜度，並且在自測階段測試較為充分，故最終提交的作業里沒有出現性能問題。

四、請針對下頁ppt內容對Network進行擴展，並給出相應的JML規格

​ 假設出現了幾種不同的Person

  • Advertiser：持續向外發送產品廣告
  • Producer：產品生產商，通過Advertiser來銷售產品
  • Customer：消費者，會關註廣告並選擇和自己偏好匹配的產品來購買 -- 所謂購買，就是直接通過Advertiser給相應Producer發一個購買消息
  • Person：吃瓜群眾，不發廣告，不買東西，不賣東西

如此Network可以支持市場營銷，並能查詢某種商品的銷售額和銷售路徑等 請討論如何對Network擴展，給出相關介面方法，並選擇3個核心業務功能的介面方法撰寫JML規格（借鑒所總結的JML規格模式）

首先，針對廣告和訂購兩種消息新建介面

廣告消息：繼承自Message介面，且要求type=2，（僅初始化Person1）JML如下

public interface AdMessage extends Message{
    /*@
      @ public instance model int productId;
      @ public instance model int price;
      @*/
    
    //@ public invariant socialValue == price;
    
    //@ ensures \result == productId; 
    public /*@ pure @*/ int getProductId();
    
    //@ ensures \result == price;
    public /*@ pure @*/ int getPrice();
}

訂購消息：繼承自Message介面，且要求type=3（初始化Person1和Person2），JML如下

public interface PurchaseMessage extends Message{
    /*@
      @ public instance model int productId;
      @ public instance model int quantity;
      @ public instance model int producerId;
      @*/
    
    //public invariant socialValue == quantity;
    
    //@ ensures \result == productId;
    public /*@ pure @*/ int getProductId();
    
    //@ ensures \result == quantity;
    public /*@ pure @*/ int getQuantity();
    
    //@ ensures \result == producerId;
    public /*@ pure @*/ int getProducerId();
}

然後考慮除Person以外的三類人員，新建介面

public interface Advertiser extends Person{
   	/*@ 
   	  @ public instance model Producer[] producers; //所經銷的生產廠家
   	  @ public instance model int[] products;//所經銷的產品號
   	  @*/
    
    // ensures \result == (\exists int i; 0 <= i && i < producers.length(); producers[i].getId() == id);
   	public /*@ pure @*/ boolean containsProducer(int id);
    
    // ensures \result == (\exists int i; 0 <= i && i< products.length(); products[i] == id);
    public /*@ pure @*/ boolean containsProduct(int id);
    
}
public interface Producer extends Person{
    /*@
      @ public instance model Advertiser[] advertisers;  //經銷商
      @ public instance model int[] products;//所生產的產品號
      @*/
    // ensures \result == (\exists int i; 0 <=i && i < advertisers.length(); advertisers[i].getId() == id);
    public /*@ pure @*/ boolean containsAdvertiser(int id);
    
    // ensures \result == (\exists int i; 0 <= u && i< products.length(); products[i] == id);
    public /*@ pure @*/ boolean containsProduct(int id);
}
putlic interface Customer extends Person{
}

然後在Network中新增四個方法

  • 發送廣告：考慮Advertiser也屬於普通用戶（繼承自Person），而並非微店，所以實際微信中更類似於“朋友圈營銷”的廣告方式，因此這裡限定TA只能向有好友(isLinked)的Customer和吃瓜群眾發送廣告。
  • 發送訂單
  • 查詢某種商品的銷售額
  • 查詢某種商品的銷售路徑：輸出為一個四元組的列表，每一個四元組為（生產者、經銷商、消費者、數量）
//四元組,這裡就不用JML了
public class Item{
    private Person producer;
    private Person advertiser;
    private Person customer;
    private int quantity;
    private int productId;
    public Item(Person producer, Person advertiser, Person customer, int quantity, int productId)
    {
        this.producer = producer;
        this.advertiser = advertiser;
        this.customer = customer;
        this.quantity = quantity;
        hits.productId = productId;
    }
    public int getId()
    {
        return productId;
    }
}

方法的JML

public interface Network
{
    //省略已有的public instance model
    
    /*@ public instance model non_null Item[] paths;
        public instance model non_null int[] productSoldout;
      @*/
    
   //省略已有的方法
    
    /*@ public normal_behavior
      @ requires containsMessage(id) && (getMessage(id) instanceof AdMessage）&&(getMessage(id).getType==2) && (getMessage(id).getPerson1() instanceof Advertiser)
      @ assignable getMessage(id).getPerson1().socialValue
      @ assignable people[*].socialValue, people[*].messages
      @ ensures \old(getMessage(id)).getPerson1().getSocialValue() ==
      @ \old(getMessage(id).getPerson1().getSocialValue()) + \old(getMessage(id)).getSocialValue()
      @ ensures (\forall int i; 0 <= i && i < \old(people).length() && \old(people[i]).isLinked(getMessage(id).getPerson1()) && !(\old(people[i]) instanceof Advertiser) && !(\old(people[i]) instanceof Producer); \old(people[i]).getSocialValue() == \old(people[i].getSocialValue()) + \old(getMessage(id)).getSocialValue();
      @ ensures (\forall int i; 0 <=i && i < \old(people).length() && \old(people[i]).isLinked(getMessage(id).getPerson1()) && !(\old(people[i]) instanceof Advertiser) && !(\old(people[i]) instanceof Producer); 
      (\forall int j; 0 <= j && j < \old(people[i].getMessages().size()); \old(people[i]).getMessages().get(i+1) = \old(people[i].getMessages().get(i))));
      @ ensures (\forall int i; 0 <=i && i < \old(people).length() && \old(people[i]).isLinked(getMessage(id).getPerson1()) && !(\old(people[i]) instanceof Advertiser) && !(\old(people[i]) instanceof Producer); \old(people[i]).getMessages().get(0).equals(\old(getMessage(id)));
      @ also
      @ public exceptional_behavior
      @ signals (MessageIdNotFoundException e) !containsMessage(id);
      @ signals (InvalidMessageTypeException e) containsMessage(id) && (!(getMessage(id) instanceof AdMessage) || ((getMessage(id) instanceof AdMessage) && getMessage(id).getType!=2));
      @ signals (InvalidPersonTypeException e) containsMessage(id) && (getMessage(id) instanceof AdMessage) && (getMessage(id).getType==2) && !(getMessage(id).getPerson1() instanceof Advertiser)
      @*/
    public void sendAdMessage(int id) throws MessageIdNotFoundException, InvalidMessageTypeException, InvalidPersonTypeException;
    
    /*@ public normal_behavior
      @ requires containsMessage(id) && (getMessage(id) instanceof AdMessage) && (getMessage(id).getType==3) && ((getMessage(id).getPerson1() instanceof Customer) && (getMessage(id).getPerson2() instanceof Advertiser) && (getPerson(getMessage(id).getProducerId()) instanceof Producer)) && (((Advertiser)getMessage(id).getPerson2()).containsProduct(getMessage(id).getProductId()));
      @ assignable getMessage(id).getPerson2().messages, paths, productSoldout;
      @ ensures (\forall int i; 0 <= i && i < \old(getMessage(id).getPerson2()).getMessages().size());
      \old(getMessage(id).getPerson2()).getMessages().get(i+1) = \old(getMessage(id).getPerson2().getMessages().get(i));
      @ ensures \old(getMessage(id).getPerson2()).getMessages().get(0).equals(getMessage(id));
      @ ensures \old(getMessage(id).getPerson2()).getMessages().size() == \old(getMessage(id).getPerson2().getMessages().size()) + 1;
      @ ensures productSoldout[((PurchaseMessage)getMessage(id)).getProductId()] == \old(productSoldout[((PurchaseMessage)getMessage(id)).getProductId()]) + ((PurchaseMessage)getMessage(id)).getQuantity();
      @ ensures (\exist int i; 0 <= i && i < paths.length(); paths[i].equals(new Item(getPerson(((PurchaseMessage)getMessage(id)).getProducerId(), getMessage().getPerson2(), getMessage().getPerson1(), ((PurchaseMessage)getMessage(id)).getQuantity(), ((PurchaseMessage)getMessage(id)).getProductId());
      @ also
      @ public exceptional_behavior
      @ signals (MessageIdNotFoundException e) !containsMessage(id);
      @ signals (InvalidMessageTypeException e) containsMessage(id) && (!(getMessage(id) instanceof PurchaseMessage) || ((getMessage(id) instanceof PurchaseMessage) && getMessage(id).getType!=2));
      @ signals (InvalidPersonTypeException e) containsMessage(id) && (getMessage(id) instanceof AdMessage) && (getMessage(id).getType==3) && (!(getMessage(id).getPerson1() instanceof Customer) || !(getMessage(id).getPerson2() instanceof Advertiser) || (!getPerson(getMessage(id).getProducerId()) instanceof Producer));
      @ signals (ProductIdNotFoundException e) containsMessage(id) && (getMessage(id) instanceof AdMessage) && (getMessage(id).getType==3) && ((getMessage(id).getPerson1() instanceof Customer) && (getMessage(id).getPerson2() instanceof Advertiser) && (getPerson(getMessage(id).getProducerId()) instanceof Producer)) && !(((Advertiser)getMessage(id).getPerson2()).containsProduct(getMessage(id).getProductId()));
      @*/
    public void sendPurchaseMessage(int id) throws MessageIdNotFoundException, InvalidMessageTypeException, InvalidPersonTypeException, ProductIdNotFoundException;

    /*@ public normal_behavior
	  @ ensures \result == productSoldout[id];
      @*/
    public /*@ pure @*/ int getSaledata(int id);
    
    /*@ public normal_behavior
      @ ensures (\forall int i; 0 <=i && i < paths.length() && paths[i].getId() == id;
      	\result.contains(paths[i]));
      @*/
    public List<Item> getSalePath(int id);
}

五、本單元學習體會

​ 這個單元相比於前兩個單元的設計和編碼工作量確實小了不少，不過初次接觸JML規格的時候，會有一種“帶著鐐銬跳舞”的感覺——首先JML給出的各種約束和限制是必須要滿足的，在滿足的基礎上，還要去思考如何提高效率，比如選擇怎麼樣的容器，選擇怎麼樣的演算法。

​ 最為重要的是，這個單元的測試與前面兩個單元的很大不同在於所謂的“題目數據限制”可謂是“無處不在”，因為任何一處JML語句都不能忽視。一方面可以用Junit工具來顯式地驗證一些前置後置條件的滿足情況，另一方面對於編寫數據生成器進行大量測試而言，能不能擊中缺陷其實是很大的問題。典型的例子就是上面提到了，即便做了大量的普遍測試（比如上萬組），但是因為普遍數據生成器構造的不足，觸發不了bug，那麼某種程度上自測就白測了。

​ 因此，我覺得黑盒白盒測試（包括代碼通讀）都要認真做，不可偏廢。尤其是現在還沒有自動根據JML生成Junit測試的情況下，即便是編寫數據生成器，也還是基於人工對JML的語義理解，如果對JML語義理解有偏差，那麼就談不上測試的有效性。


您的分享是我們最大的動力!

-Advertisement-
Play Games
更多相關文章
  • HTML快速入門第一課
    非常感謝小趙同學給我反饋的這個 Bug
  • Python使用ch-orm對ClickHouse簡單查詢及寫入
    前言 眾所周知，spring對於java程式員來說是一個及其重要的後端框架，幾乎所有的公司都會使用的框架，而且深受廣大面試官的青睞。所以本文就以常見的一個面試題"spring bean的生命周期"為切入點，從源碼的角度帶領大家來看一看 spring bean到底是如何創建的 。spring bean ...
  • springboot自動裝配原理探究
    springboot自動裝配原理探究 結論： SpringBoot啟動會載入大量的自動配置類 我們看我們需要的功能有沒有在SpringBoot預設寫好的自動配置類當中； 我們再來看這個自動配置類中到底配置了哪些組件；（只要我們要用的組件存在在其中，我們就不需要再手動配置了） 給容器中自動配置類添加組 ...
  • VScode中配置Java環境
    vscode 中配置Java環境 轉載說明：本篇文檔原作者[@火星動力猿]，文檔出處來自嗶哩嗶哩-【教程】VScode中配置Java運行環境 轉載請在開頭或顯眼位置標註轉載信息。 1.下載VScode 官網地址：https://code.visualstudio.com/ （點鏈接時按下Ctrl，不 ...
  • 【SSM框架】SpringMVC筆記 --- 彙總
    SpringMVC 是基於 MVC 開發模式的框架，用來優化控制器，是 Spring 家族的一員，同時它也具備 IOC 和 AOP ...
  • python常用標準庫（os系統模塊、shutil文件操作模塊）
    一、填空題 在種群增長預測問題中,若資源環境等因素是有限的,則應使用的微分方程模型為 Logistic模型 某種群分為 4 個年齡組, 各組的繁殖率分別為 0, 0.8, 1.8, 0.2, 存活率分別為 0.5, 0.7, 0.9, 0. 現各組的數量均為 100, 則該種群的的穩定分佈向量為 解 ...
  • 模擬併發的 4 種方式，還有誰不會？？
    一、Postman Postman 是一個款 HTTP 請求模擬工具 首先演示一下 Postman 最基本的使用，創建一個 Spring Boot 項目，測試的代碼如下： import org.springframework.web.bind.annotation.GetMapping; impor ...
  • Java 線程創建與常用方法
    ## 進程與線程的區別 - 進程基本上相互獨立的，而線程存在於進程內，是進程的一個子集 - 進程擁有共用的資源，如記憶體空間等，供其內部的線程共用 - 進程間通信較為複雜 - 同一臺電腦的進程通信稱為 IPC（Inter-process communication） - 不同電腦之間的進程... ...
一周排行
    -Advertisement-
    Play Games
  • 移動開發（一）：使用.NET MAUI開發第一個安卓APP
    移動開發（一）：使用.NET MAUI開發第一個安卓APP 對於工作多年的C#程式員來說，近來想嘗試開發一款安卓APP，考慮了很久最終選擇使用.NET MAUI這個微軟官方的框架來嘗試體驗開發安卓APP，畢竟是使用Visual Studio開發工具，使用起來也比較的順手，結合微軟官方的教程進行了安卓 ...
  • wpf ToggleButton選中效果和一個登錄界面
    前言 QuestPDF 是一個開源 .NET 庫，用於生成 PDF 文檔。使用了C# Fluent API方式可簡化開發、減少錯誤並提高工作效率。利用它可以輕鬆生成 PDF 報告、發票、導出文件等。 項目介紹 QuestPDF 是一個革命性的開源 .NET 庫，它徹底改變了我們生成 PDF 文檔的方 ...
  • 彈幕樹洞項目功能新增篇
    項目地址 項目後端地址： https://github.com/ZyPLJ/ZYTteeHole 項目前端頁面地址： ZyPLJ/TreeHoleVue (github.com) https://github.com/ZyPLJ/TreeHoleVue 目前項目測試訪問地址： http://tree ...
  • 第27篇 sqlserver2022詳細安裝步驟
    話不多說，直接開乾 一.下載 1.官方鏈接下載： https://www.microsoft.com/zh-cn/sql-server/sql-server-downloads 2.在下載目錄中找到下麵這個小的安裝包 SQL2022-SSEI-Dev.exe，運行開始下載SQL server； 二. ...
  • .NET 開源高性能 MQTT 類庫
    前言 隨著物聯網（IoT）技術的迅猛發展，MQTT（消息隊列遙測傳輸）協議憑藉其輕量級和高效性，已成為眾多物聯網應用的首選通信標準。 MQTTnet 作為一個高性能的 .NET 開源庫，為 .NET 平臺上的 MQTT 客戶端與伺服器開發提供了強大的支持。 本文將全面介紹 MQTTnet 的核心功能 ...
  • Serilog文檔翻譯系列（六） - 可用的接收器、增強器、格式化輸出
    Serilog支持多種接收器用於日誌存儲，增強器用於添加屬性，LogContext管理動態屬性，支持多種輸出格式包括純文本、JSON及ExpressionTemplate。還提供了自定義格式化選項，適用於不同需求。 ...
  • 警惕 Visual Studio 屬性求值副作用導致邏輯不符合預期
    目錄簡介獲取 HTML 文檔解析 HTML 文檔測試參考文章 簡介 動態內容網站使用 JavaScript 腳本動態檢索和渲染數據，爬取信息時需要模擬瀏覽器行為，否則獲取到的源碼基本是空的。 本文使用的爬取步驟如下： 使用 Selenium 獲取渲染後的 HTML 文檔 使用 HtmlAgility ...
  • [使用目前最新版]HybridCLR6.9.0+YooAsset2.2.4實現純C# Unity熱更新方案 (一)
    1.前言 什麼是熱更新 游戲或者軟體更新時，無需重新下載客戶端進行安裝，而是在應用程式啟動的情況下，在內部進行資源或者代碼更新 Unity目前常用熱更新解決方案 HybridCLR，Xlua，ILRuntime等 Unity目前常用資源管理解決方案 AssetBundles，Addressable， ...
  • 在 ASP.NET Core Web API 中使用操作篩選器統一處理通用操作
    本文章主要是在C# ASP.NET Core Web API框架實現向手機發送驗證碼簡訊功能。這裡我選擇是一個互億無線簡訊驗證碼平臺，其實像阿裡雲，騰訊雲上面也可以。 首先我們先去 互億無線 https://www.ihuyi.com/api/sms.html 去註冊一個賬號 註冊完成賬號後，它會送 ...
  • 第28篇 如何.net中實現高效可靠數據同步api
    通過以下方式可以高效，並保證數據同步的可靠性 1.API設計 使用RESTful設計，確保API端點明確，並使用適當的HTTP方法（如POST用於創建，PUT用於更新）。 設計清晰的請求和響應模型，以確保客戶端能夠理解預期格式。 2.數據驗證 在伺服器端進行嚴格的數據驗證，確保接收到的數據符合預期格 ...
所有分類