日期:2022年5月25日 註:本博客僅供參考 概念與思路 貪心演算法是指在對某一問題求解時,總是作出當前情況下的最優選擇。因此,貪心演算法考慮的不是整個問題的最優解,演算法得到的是在某一局部環境下的最優解。 貪心演算法的一般思路為: 把要求解的問題分為若幹個子問題; 對每個子問題求解,得到子問題的局部最優 ...
日期:2022年5月25日
註:本博客僅供參考
概念與思路
貪心演算法是指在對某一問題求解時,總是作出當前情況下的最優選擇。因此,貪心演算法考慮的不是整個問題的最優解,演算法得到的是在某一局部環境下的最優解。
貪心演算法的一般思路為:
- 把要求解的問題分為若幹個子問題;
- 對每個子問題求解,得到子問題的局部最優解;
- 把得到的局部最優解合為原來問題的一個解。
註意事項(尤為重要)
- 貪心演算法能省去要窮盡所有可能二耗費的大量時間,但它沒有考慮整個問題下的情景,因此通過該演算法得到的答案,不能確定是否為整個問題的最優解。也就是說,如果要使用貪心演算法,應該在證明出通過貪心得出的答案就是最優解後再使用。
- 貪心演算法一般只用於求最大或最小值。
- 貪心演算法只能確定某些問題的可行性範圍。
代碼與應用
部分背包問題(P2240)
題目描述
阿裡巴巴走進了裝滿寶藏的藏寶洞。藏寶洞裡面有N(N≤100)堆金幣,第i堆金幣的總重量和總價值分別是 mi,vi(1≤mi,vi≤100)。阿裡巴巴有一個承重量為T(T≤1000)的背包,但並不一定有辦法將全部的金幣都裝進去。他想裝走儘可能多價值的金幣。所有金幣都可以隨意分割,分割完的金幣重量價值比(也就是單位價格)不變。請問阿裡巴巴最多可以拿走多少價值的金幣?
輸入格式
第一行兩個整數 N,T。
接下來N行,每行兩個整數 mi,vi。
輸出格式
一個實數表示答案,輸出兩位小數。
代碼
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=110; 4 int n,t; 5 struct node{ 6 int m; 7 int v; 8 }; 9 node a[N]; 10 bool operator <(node a,node b){ 11 return a.v*b.m>b.v*a.m; 12 /*用金幣價值與金幣質量的比值來比較不同金幣的實際價值 14 return a.v*b.m>b.v*a.m的效果等同於return a.v/a.m>b.v/b.w,但由於在C++中“/”意為整除,所以需要使用其他方法代替除法*/ 15 } 16 int main(){ 17 scanf("%d%d",&n,&t); 18 for(int i=1;i<=n;++i) 19 { 20 scanf("%d%d",&a[i].m,&a[i].v); 21 } 22 sort(a+1,a+1+n);//重定義的的“<”會在這裡用到 23 double ans=0; 24 for(int i=1;i<=n;++i) 25 { 26 if(a[i].m<=t)//當金幣質量小於背包能容納的剩餘質量時,將這堆金幣全部放進去 27 { 28 ans+=a[i].v; 29 t-=a[i].m; 30 }else{//當金幣質量大於背包能容納的剩餘質量時,用這種金幣將背包的剩餘部分填滿並結束迴圈 31 ans+=1.0*t*a[i].v/a[i].m; 32 break; 33 } 34 } 35 printf("%.2lf",ans); 36 return 0; 37 }
排隊接水(P1223)
題目描述
有n個人在一個水龍頭前排隊接水,假如每個人接水的時間為Ti,請編程找出這n個人排隊的一種順序,使得n個人的平均等待時間最小。
輸入格式
第一行為一個整數n。
第二行n個整數,第i個整數Ti 表示第i個人的等待時間Ti。
輸出格式
輸出文件有兩行,第一行為一種平均時間最短的排隊順序;第二行為這種排列方案下的平均等待時間(輸出結果精確到小數點後兩位)。
代碼
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=1000100; 4 int n; 5 double ave=0; 6 struct node{ 7 int t; 8 int code; 9 }; 10 bool operator <(node a,node b){ 11 return a.t<b.t;//升序排列 12 } 13 node T[N]; 14 int main(){ 15 scanf("%d",&n); 16 for(int i=1;i<=n;++i) 17 { 18 scanf("%d",&T[i].t); 19 T[i].code=i; 20 } 21 sort(T+1,T+1+n); 22 for(int i=1;i<=n;++i) 23 { 24 for(int j=0;j<i;++j) 25 { 26 ave+=T[j].t; 27 } 28 printf("%d ",T[i].code); 29 } 30 ave/=n;//平均等待時間為所有人需要等待的時間與人數的比值 31 printf("\n%.2lf",ave); 32 return 0; 33 }
均分紙牌(P1031)
題目描述
有NN堆紙牌,編號分別為 1,2,…,N。每堆上有若幹張,但紙牌總數必為N的倍數。可以在任一堆上取若幹張紙牌,然後移動。
移牌規則為:在編號為1堆上取的紙牌,只能移到編號為2的堆上;在編號為N的堆上取的紙牌,只能移到編號為N-1的堆上;其他堆上取的紙牌,可以移到相鄰左邊或右邊的堆上。
現在要求找出一種移動方法,用最少的移動次數使每堆上紙牌數都一樣多。
例如N=4,4堆紙牌數分別為:
①9②8③17④6
移動3次可達到目的:
從 ③ 取4張牌放到 ④ (9,8,13,10)-> 從 ③ 取3張牌放到 ②(9,11,10,10)-> 從 ② 取1張牌放到①(10,10,10,10)。
輸入格式
兩行
第一行為:N(N堆紙牌,1≤N≤100)。
第二行為:A1,A2, … ,An (N堆紙牌,每堆紙牌初始數,1≤Ai≤10000)。
輸出格式
一行:即所有堆均達到相等時的最少移動次數。
代碼
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=110; 4 int n,a[N],ave=0,sum=0; 5 int main(){ 6 scanf("%d",&n); 7 for(int i=1;i<=n;++i) 8 { 9 scanf("%d",&a[i]); 10 ave+=a[i]; 11 } 12 ave/=n;//紙牌平均數恆為定值 13 for(int i=1;i<=n;++i) 14 { 15 if(a[i]!=ave)//如果這堆紙牌不是平均值,向右邊放a[i+1]-ave張紙牌 16 { 17 a[i+1]+=a[i]-ave; 18 ++sum; 19 } 20 } 21 printf("%d",sum); 22 return 0; 23 }
鋪設道路(P5019)
題目描述
春春是一名道路工程師,負責鋪設一條長度為n的道路。
鋪設道路的主要工作是填平下陷的地表。整段道路可以看作是n塊首尾相連的區域,一開始,第i塊區域下陷的深度為di。
春春每天可以選擇一段連續區間[L,R],填充這段區間中的每塊區域,讓其下陷深度減少1。在選擇區間時,需要保證,區間內的每塊區域在填充前下陷深度均不為0。
春春希望你能幫他設計一種方案,可以在最短的時間內將整段道路的下陷深度都變為0。
輸入格式
輸入文件包含兩行,第一行包含一個整數n,表示道路的長度。 第二行包含n個整數,相鄰兩數間用一個空格隔開,第i個整數為di。
輸出格式
輸出文件僅包含一個整數,即最少需要多少天才能完成任務。
代碼
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=100100; 4 int n,d[N],sum=0; 5 int main(){ 6 scanf("%d",&n); 7 for(int i=1;i<=n;++i) 8 { 9 scanf("%d",&d[i]); 10 } 11 sum+=d[1]; 12 for(int i=2;i<=n;++i) 13 { 14 if(d[i]>d[i-1]) 15 { 16 sum+=d[i]-d[i-1];//如果後面大於前面,則共有d[i]-d[i-1]層需要單獨填掉(小於的部分可以和前面一起填掉) 17 } 18 } 19 printf("%d",sum); 20 return 0; 21 }
線段覆蓋(P1803)
題目描述
現在各大oj上有n個比賽,每個比賽的開始、結束的時間點是知道的。
yyy認為,參加越多的比賽,noip就能考的越好(假的)。
所以,他想知道他最多能參加幾個比賽。
由於y是蒟蒻,如果要參加一個比賽必須善始善終,而且不能同時參加2個及以上的比賽。
輸入格式
第一行是一個整數n,接下來n行每行是2個整數 ai,bi(ai<bi),表示比賽開始、結束的時間。
輸出格式
一個整數,表示最多參加的比賽數目。
代碼
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=1000100; 4 int n,sum=0,now=0; 5 struct node{ 6 int a; 7 int b; 8 }; 9 bool operator <(node A,node B){ 10 return A.b<B.b; 11 } 12 node m[N]; 13 int main(){ 14 scanf("%d",&n); 15 for(int i=1;i<=n;++i) 16 { 17 scanf("%d%d",&m[i].a,&m[i].b); 18 } 19 sort(m+1,m+n+1); 20 sum=1,now=1;//選中排序後的第一個比賽 21 for(int i=2;i<=n;++i) 22 { 23 if(m[i].a>=m[now].b)//如果下一個比賽開始時間在正在參加的比賽結束時間之後(相等也可以),則選中這個比賽 24 { 25 ++sum; 26 now=i; 27 } 28 } 29 printf("%d",sum); 30 return 0; 31 }
雷達安裝(P1325)
題目描述
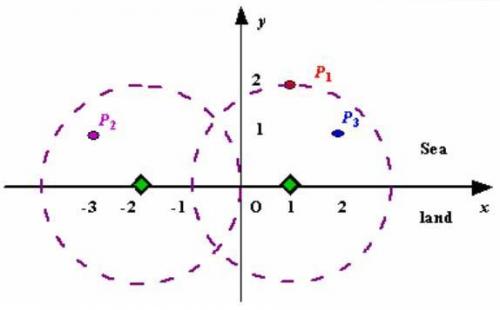
假設海岸線是一條無限延伸的直線。它的一側是陸地,另一側是海洋。每一座小島是在海面上的一個點。雷達必須安裝在陸地上(包括海岸線),並且每個雷達都有相同的掃描範圍d。你的任務是建立儘量少的雷達站,使所有小島都在掃描範圍之內。
數據使用笛卡爾坐標系,定義海岸線為x軸。在x軸上方為海洋,下方為陸地。
如圖:
輸入格式
第一行包括2個整數n和d,n是島嶼數目,d是雷達掃描範圍。
接下來n行為島嶼坐標。
輸出格式
一個整數表示最少需要的雷達數目,若不可能覆蓋所有島嶼,輸出-1。
代碼
1 #include<bits/stdc++.h> 2 using namespace std; 3 const int N=1100; 4 int n,d,x[N],y[N],now=0,sum=0; 5 struct node{ 6 double L; 7 double R; 8 }; 9 bool operator <(node a,node b){ 10 return a.R<b.R; 11 } 12 node a[N]; 13 int main(){ 14 scanf("%d%d",&n,&d); 15 for(int i=1;i<=n;++i) 16 { 17 scanf("%d%d",&x[i],&y[i]); 18 if(y[i]>d)//如果小島的縱坐標比雷達的半徑還要大,那麼就覆蓋不到這個小島,輸出-1並結束程式 19 { 20 printf("%d",-1); 21 return 0; 22 } 23 a[i].L=x[i]-sqrt(pow(d,2)-pow(y[i],2)); 24 a[i].R=x[i]+sqrt(pow(d,2)-pow(y[i],2)); 25 //計算出雷達可以覆蓋到這個小島的極限範圍區間(用勾股定理計算,斜邊為d,一個直角邊為y[i]) 26 } 27 sort(a+1,a+1+n); 28 sum=1,now=1;//覆蓋到第一個小島,安放第一個雷達 29 for(int i=2;i<=n;++i) 30 { 31 if(a[i].L>a[now].R)//如果這兩個區間沒有公共部分,則安放下一個雷達 32 { 33 ++sum; 34 now=i; 35 } 36 } 37 printf("%d",sum); 38 return 0; 39 }